Historians everywhere are shocked by the recent discovery that many of our greatest thinkers and poets had first expressed their thoughts and ideas in the language of first-order predicate logic, and sometimes modal logic, rather than in natural language. Some early indications of this were revealed in the pioneering historical research of Henle, Garfield and Tymoczko, in their work Sweet Reason:
We now know that the phenomenon is widespread! As shown below, virtually all of our cultural leaders have first expressed themselves in the language of first-order predicate logic, before having been compromised by translations into the vernacular.
$\neg\lozenge\neg\exists s\ G(i,s)$
$(\exists x\ x=i)\vee\neg(\exists x\ x=i)$
.jpg#/media/File:Lorde_Laneway_7_(cropped).jpg "De Annette Geneva - Flickr: LORDE, CC BY-SA 2.0")
$\left(\strut\neg\exists t\ \exists d\ \strut D(d)\wedge F(d)\wedge S_t(i,d)\right)\wedge\left(\strut\neg\exists t\ w\in_t \text{Ro}\right)\wedge\left(\strut \text{Ru}(i,y)\to \lozenge\text{C}(y,i,qb)\wedge \text{Ru}(i)\wedge\text{Ru}(i)\wedge\text{Ru}(i)\wedge\text{Ru}(i)\right)$
$\exists!t\ T(t) \wedge \forall t\ (T(t)\to G(t))$
$\neg B_i \exists g\ G(g)$
$\forall b\ \left(\strut G(b)\wedge B(b)\to \exists x\ (D(b,x)\wedge F(x))\right)$
$(\exists!w\ W_1(w)\wedge W_2(w)), \ \ \exists w\ W_1(w)\wedge W_2(w)\wedge S(y,w)$?
$\exists s\ Y(s)\wedge S(s)\wedge \forall x\ L(x,s)$
$\exists p\ \left[\forall c\ (c\neq p\to G(c))\right]\wedge\neg G(p)$
$\exists l\ \left[L(l)\wedge \Box_l\left({}^\ulcorner\,\forall g\ \text{Gl}(g)\to \text{Gd}(g){}^\urcorner\right)\wedge\exists s\ \left(SH(s)\wedge B(l,s)\right)\right]$
$(\forall p\in P\ \exists c\in\text{Ch}\ c\in p)\wedge(\forall g\in G\ \exists c\in\text{Cr}\ c\in g)$
$\forall x (F(w,x)\leftrightarrow x=F)$
$B\wedge \forall x\ \left[S(x)\wedge T(x)\to \exists!w\ W(w)\wedge\text{Gy}(x,w)\wedge\text{Gi}(x,w)\right]$
$\exists!x\ D(x)\wedge D(\ {}^\ulcorner D(i){}^\urcorner\ )$
$\forall f\ \forall g\ \left(\strut H(f)\wedge H(g)\to f\sim g\right)\wedge\forall f\ \forall g\ \left(\strut\neg H(f)\wedge \neg H(g)\to \neg\ f\sim g\right)$
$\exists w\ \left(\strut O(w)\wedge W(w)\wedge\exists s\ (S(s)\wedge L(w,s))\right)$
$C(i)\to \exists x\ x=i$
$\neg\neg\left(\strut H(y)\wedge D(y)\right)$
$\neg (d\in K)\wedge\neg (t\in K)$
.jpg#/media/File:Meat_Loaf_in_performance_(New_York,_2004).jpg "By Mr.Mushnik at English Wikipedia, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1537525")
$W(i,y)\wedge N(i,y)\wedge\neg\neg\lozenge L(i,y)\wedge \left(\strut \neg\ \frac23<0\to\neg S(y)\right)$
$\lozenge \text{CL}(i)\wedge\lozenge C(i)\wedge \lozenge (\exists x\ x=i)\wedge B(i)$
$\forall x\ K_x({}^\ulcorner \forall m\ \left[M(m)\wedge S(m)\wedge F(m)\to\Box\ \exists w\ M(m,w)\right]{}^\urcorner)$
.jpg#/media/File:Theodor_Seuss_Geisel_(01037v).jpg)
$\forall e\forall h\ \left(\strut G(e)\wedge E(e)\wedge H(h)\to \neg L(i,e,h)\right)$
$\forall p\ \Box\text{St}(p)$
$\lozenge^w_i\ \forall g\in G\ \lozenge (g\in C)$
$\forall m\ (a\leq_C m)$
$\forall t\ (p\geq t)\wedge \forall t\ (p\leq t)$
.jpg#/media/File:Emily_Dickinson_daguerreotype_(cropped).jpg)
$\forall x\ (F(x)\iff x=h)$
$(\forall x\ \forall y\ x=y)\wedge(\exists x\ \exists y ([\![x=x]\!]>[\![y=y]\!]))$
$\forall p\ \left(\strut\neg W(p)\to \neg S(p)\right)$
$\exists x\Box\Box x\wedge \exists x\Box\neg\Box x\wedge\exists x\neg\Box\neg\Box x$
.jpg)
$\forall p \left(\strut E(p)\to \forall h\in H\ A(p,h)\right)$
Dear readers, in order to assist with this important historical work, please provide translations into ordinary English in the comment section below of any or all of the assertions listed above. We are interested to make sure that all our assertions and translations are accurate.
In addition, any readers who have any knowledge of additional instances of famous quotations that were actually first made in the language of first-order predicate logic (or similar) are encouraged to post comments below detailing their knowledge. I will endeavor to add such additional examples to the list.
Thanks to Philip Welch, to my brother Jonathan, and to Ali Sadegh Daghighi (in the comments) for providing some of the examples, and to Timothy Gowers for some improvements.
Please post comments or send me email if hints are desired.
∀t G(i,t)
Can you give us a hint with a little more context?
I’ve taken the Rolling Stones first-order translation that you have above and fitted it to your question that you had at the end. Here t = translations.
Ah, very good! Congratulations! (But I’ve added several more $t$ in the meantime…)
Nice. I’ve done a few of them, and have a small quibble about one (the sixth from the end). I think the last part shouldn’t be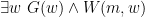
. That’s too romantic — even Platonic. However, I can’t work out how to express the real statement in first-order logic.
I’m glad you tried them! And yes, I agree that that one could be improved. Perhaps “in want of” is a modal assertion, like “it is necessary that”, and so the quotation should state that it is necessary that there exists a w with M(m,w).
I’ve changed it now to a modal assertion, which I think is better.
I liked Orwell’s “Some animals are more equal than others” (although it seems to be missing the first part that all animals are equal).
(Also, I believe the entire witch scene in Monty Python and the Holy Grail was, and still is, essentially a first-order proof of why being equivalent to duck implies being a witch.)
I have now added the first part. Thanks!
Thanks for driving attentions to this interesting project.
I think one of the above formal quotes, $\exists x\exists y (x=x>y=y)$, is trying to formalize George Orwell’s famous sentence in his Animal Farm (chapter 10):
ALL ANIMALS ARE EQUAL, BUT SOME ANIMALS ARE MORE EQUAL THAN OTHERS.
But I’m not sure whether the part “more equal than” is formalized properly. As the notion of “being more equal than another thing while all two things are equal” itself is paradoxical (and so a bit hard to comprehend at the first moment), I guess the above formal quote in the presented form is a bit ambiguous.
https://en.wikiquote.org/wiki/Animal_Farm#Chapter_10
————————-
About Dante’s quote, it is clearly referring to “Abandon All Hope Ye who Enter Here!” (Inferno: Canto III), however the translation of the formal quote (as I, a non-native English speaker, do it) is something like the following:
EVERYBODY WHO ENTERS HERE ABANDONS ALL HOPES.
Again not sure that the two formal and real quotations are completely same but in this case I think the translation to formal language is done pretty well.
————————-
Anyway I think the way ordinary people think and convince each other in their real daily life is not 100% valid according to the formal logic rules. That is why logical fallacies are such useful tools for marketers, politicians, lawyers, etc., to induce people to do what they want even when it is not the logical consequence of the presented facts necessarily!
I think human literature is not an exception and looking to the beautiful and seemingly convincing artistic reasoning in most well-known texts of human literature (and also holy texts) will reveal the fact that they are not as strong justifications as they seem when one removes all of their artistic decoration via formalizing them into predicate logic.
What remains from them is often a barely meaningful fallacy or paradox. Possibly that is why they look such fascinating because humans masochistically like to suffer their minds by thinking about paradoxes!
I guess Leo Tolstoy’s quote is this brilliant one from Anna Karenina:
“All happy families are alike; each unhappy family is unhappy in its own way.”
(The train scenes in the beginning and end of the story are unforgettable).
You might hear this in the following form as a saying too:
“All good/sane people are alike; each bad/insane person is bad/insane in its own way.”
————————
Dear Joel, following one of our discussions in mail on Victor Hugo’s Les Misérables, let me also add a favorite quote of mine from this masterwork together with its formalization, however I think the formalized form can’t reflect the true meaning behind this impressive short quote which itself is a kind of abstract for the entire novel!
THOSE WHO DO NOT WEEP, DO NOT SEE.
$\forall p (\neg W(p)\rightarrow \neg S(p))$
By the way, am I the only person who thinks the translation of logical equivalent form of the above quote, namely $\forall p (S(p)\rightarrow W(p))$, to English is less-impressive than its original “negative form” while in principle they are talking about the same concept?!
I think it goes back to some linguistic and psychological characteristics of humans who prefer some forms to another in a set of logically equivalent sentences.
Thanks, Ali, for your examples. I added the Hugo quote, which I like very much!
You are welcome! Let me also suggest a challenging quote for formalizing from far eastern literature.
It appeared in the opening of Lao Tzu’s famous book “Tao Te Ching” in which he explains the foundations of Taoism and the notion of “Tao” which literally means “way”, “path”, or “principle” of nature that all humans should live in harmony with, otherwise the result will be nothing but their suffering and sorrow:
Original text:
道可道非常道 – 名可名非常名
Transliteration:
“dào kĕ dào fēi cháng dào – míng kĕ míng fēi cháng míng”
Translation:
“The Tao that can be told is not the eternal Tao – The name that can be named is not the eternal name.”
http://www.bopsecrets.org/gateway/passages/tao-te-ching.htm
Interestingly Kanamori refers to this quote in the appendix of his book, Higher Infinite! (see page 482).
For further reading on foundations of Taoism (and other religions of India and China), I recommend the following book which I found very well-written:
http://www.amazon.com/Mans-Religions-John-B-Noss/dp/0023884703
Maybe I’m mistaken but for Eliot, shouldn’t the signs be reversed?
I think that would also make sense, but I was thinking that $x\leq_C y$ should mean that $x$ is crueller than $y$, since one prefers to think of cruel things as being nearer the bottom. Clearly one can formalize the relation either way.
Rom 3:23: $\forall x (S(x)\wedge F(x))$ which is equivalent to saying that $(\forall x S(x))\wedge(\forall x F(x))$. This example is useful to illustrating the equivalent identity $\exists(a\vee b)=(\exists a)\vee(\exists b)$ in the variety of all monadic algebras.
Thanks for the example!
Elvis Presley
I think it says
“you are nothing but a hound dog”
Rene Descartes
“I think therefore I am”
By the way this web page is pure genius.
Thanks very much! I think you’ve got those two. Any others?
Wizard of OZ Dorothy talking to Toto “We are not in Kansas anymore”
Jane Austin “It is a truth universally acknowledged ……”
I really like the Lorde lyric!
This might be worth translating back to first-order:
Titus 1 (New International Version)
12 – One of Crete’s own prophets has said it: “Cretans are always liars, evil brutes, lazy gluttons.”
13 – This saying is true.
Similar puzzles at http://web.mit.edu/puzzle/www/2006/puzzles/paris/all_for_one_and_one_for_all/puzzle.pdf (the expression at the bottom will spell out a short phrase).
May I ask what the “C” stands for in Descartes’ quote “I think; therefore, I am.”?
It stands for “cogito”, which is Latin for the verb “to think” (like the English words cognition, cognate, cogent, cogitate). The famous quotation is “Cogito ergo sum,” and you can read more at https://en.wikipedia.org/wiki/Cogito_ergo_sum.
Thank you so much!
Is the Peter Pan bit “All children grow up, expect one”?
You’ve got it! That is the opening line of Peter Pan.
All children, except one, grow up