Welcome to the Infinite-Games Workshop, beginning Autumn 2023. The past ten years has seen an explosion in the study of infinite games, for researchers are now investigating diverse infinite games, including infinite chess, infinite draughts, infinite Hex, infinite Othello, infinite Go, indeed, we seem to have research projects involving infinitary analogues of all our familiar finite games. It is an emerging research area with many new exciting results.
This autumn, we shall set the workshop off with talks on several exciting new results in infinite chess, results which settle what had been some of the big open questions in the topic, including the question of the omega one of chess—the supremum of the ordinal game values that arise—as well as a finite position with game value
The workshop talks will be run at a high level of sophistication, aimed for the most part at serious researchers currently working in this emerging area. Mathematicians, computer scientists, infinitary game theorists, all serious researchers are welcome.

All talks will take place on Zoom at meeting 968 0186 3645 (password = latex code for the first uncountable ordinal). Contact dleonessi@gc.cuny.edu for further information.
Talks will be 90 minutes, with a workshop style welcoming questions. All talks will be recorded and placed on our YouTube channel. Talks will generally be held on Thursdays at 11:00 am New York time.
Add our calendar: Infinite-Games Workshop Calendar
The workshop is being organized by myself with the assistance of Davide Leonessi.
FAll 2023 Talks
21 September 2023 11am ET
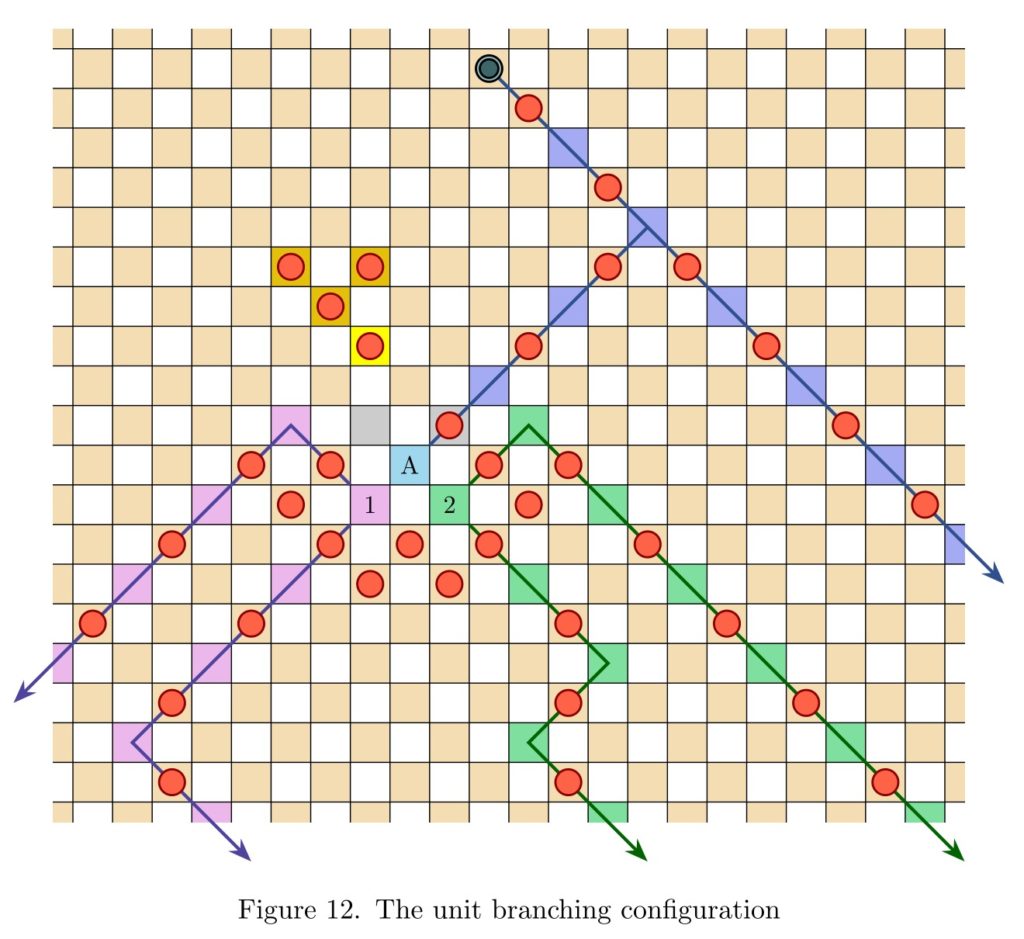
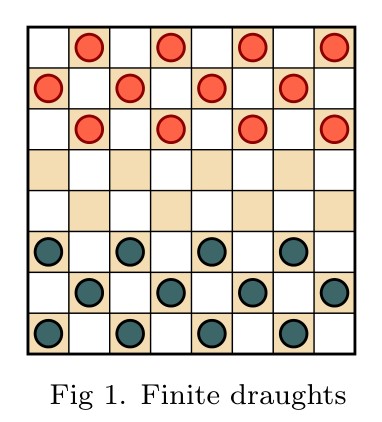
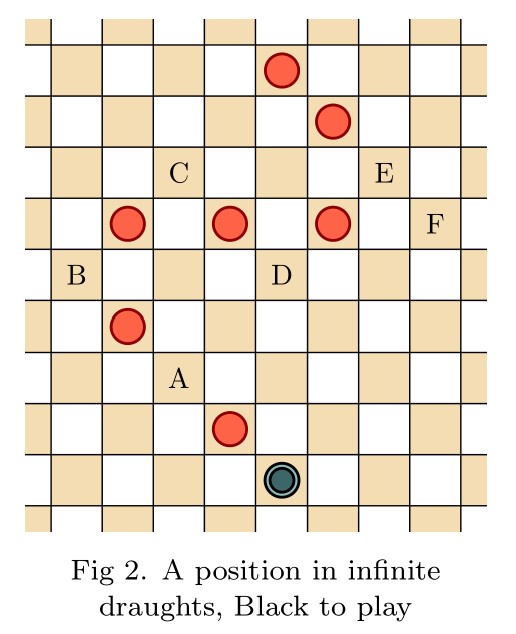
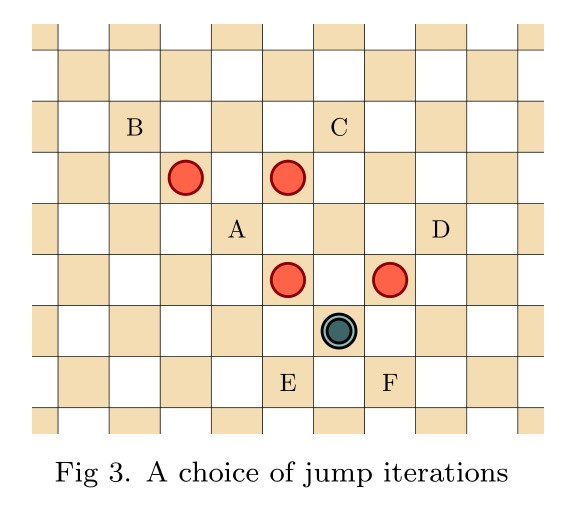
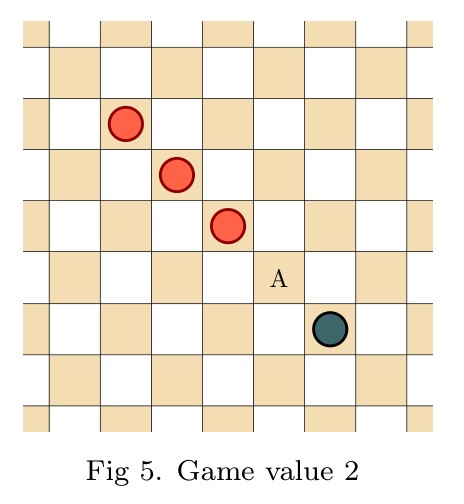
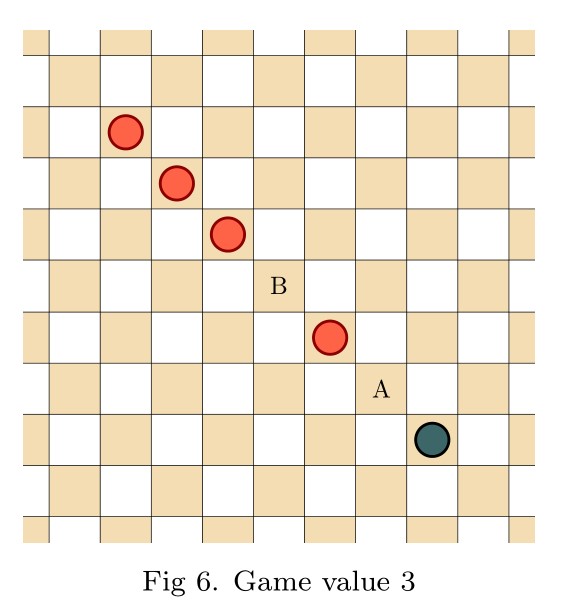
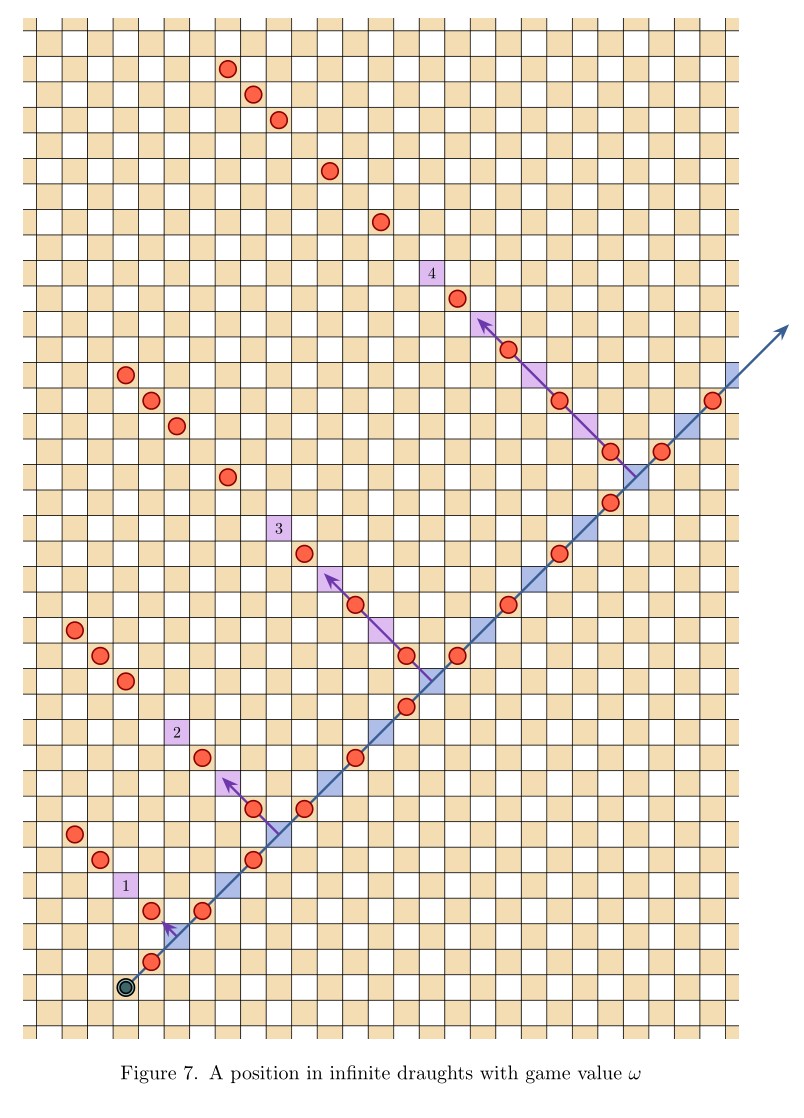
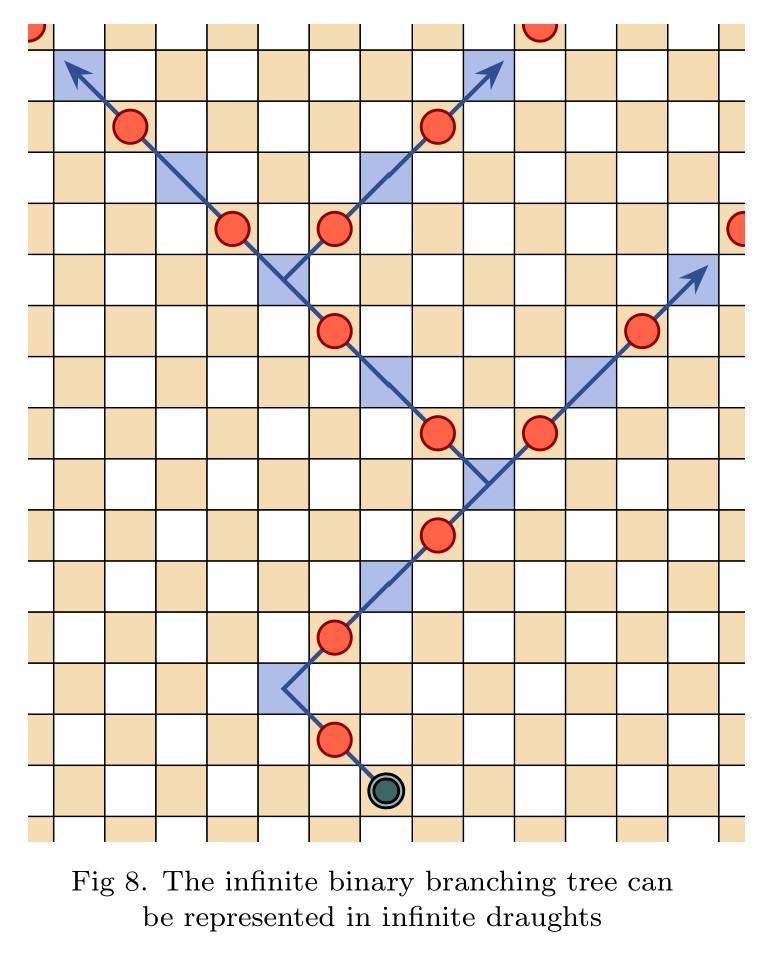
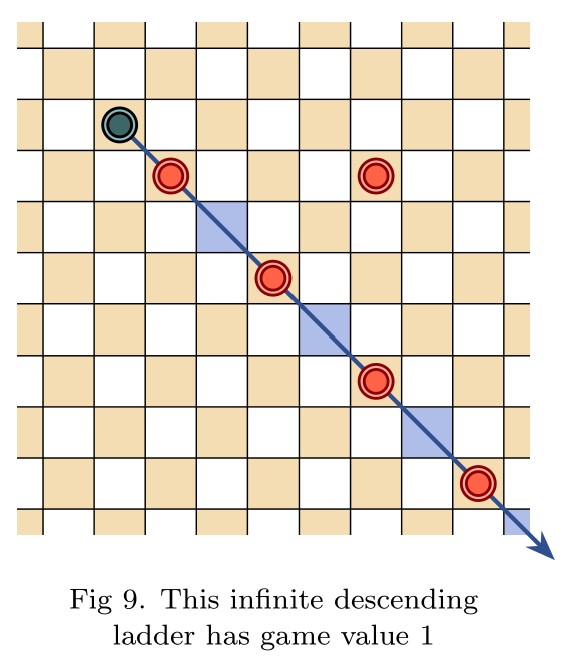
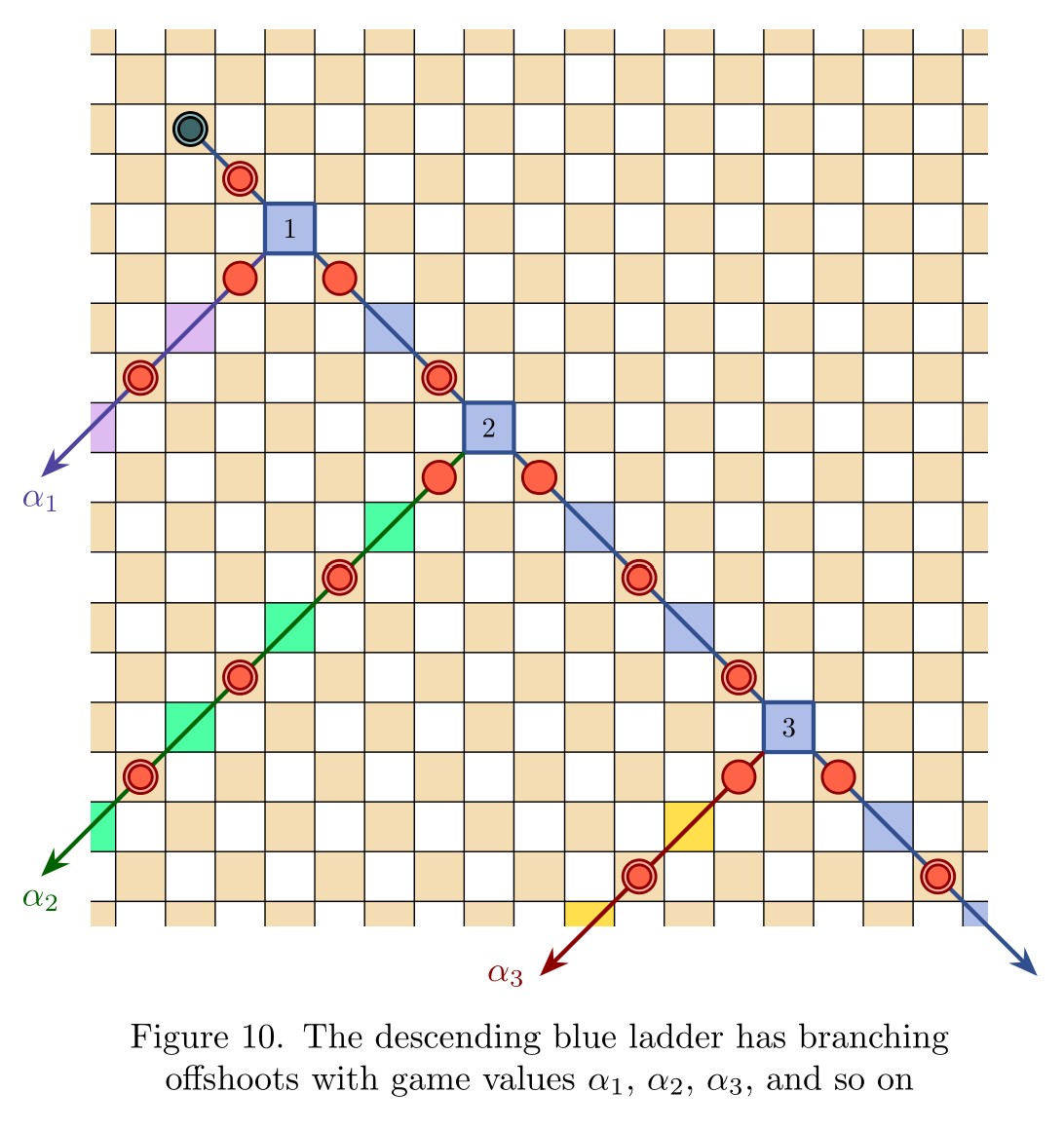
Infinite draughts: a solved open game
Davide Leonessi, The Graduate Center of the City University of New York
https://youtu.be/KZMDteLKFRI?si=_ZkSQmSlsIOmZJAx



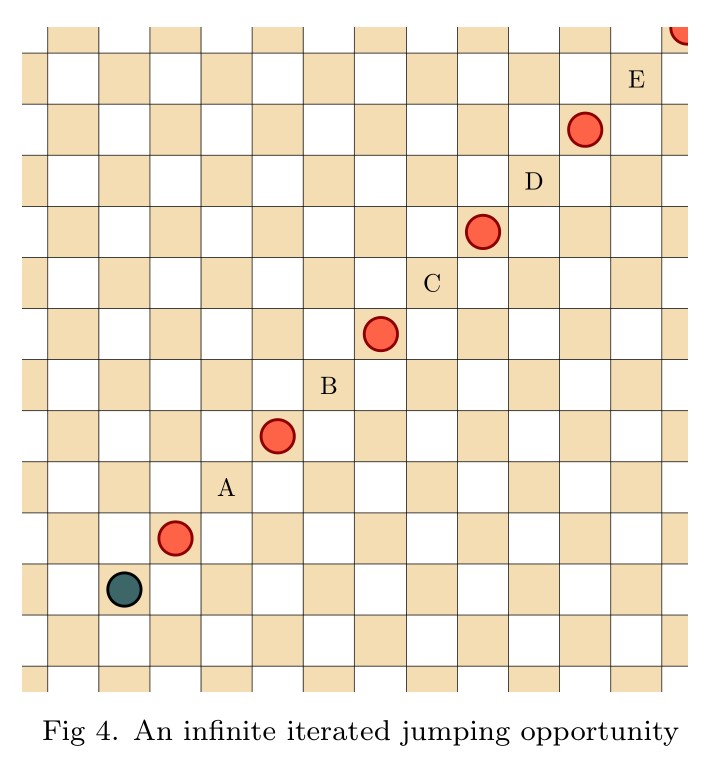
Abstract: In this talk I will introduce open infinite games, and then define a natural generalization of draughts (checkers) to the infinite planar board. Infinite draughts is an open game, giving rise to the game value phenomenon and expressing it fully—the omega one of draughts is at least true
5 October 2023 11:00 am ET
Introduction to infinite games
Joel David Hamkins, Professor of Logic, University of Notre Dame




Abstract: I shall give a general introduction to the subject and theory of infinite games, drawing upon diverse examples of infinitary games, but including also infinite chess, infinite Hex, infinite draughts, and others.
2 November 2023 11:00 am ET
Complexity of the winning condition of infinite Hex
Ilkka Törmä, University of Turku, Finland



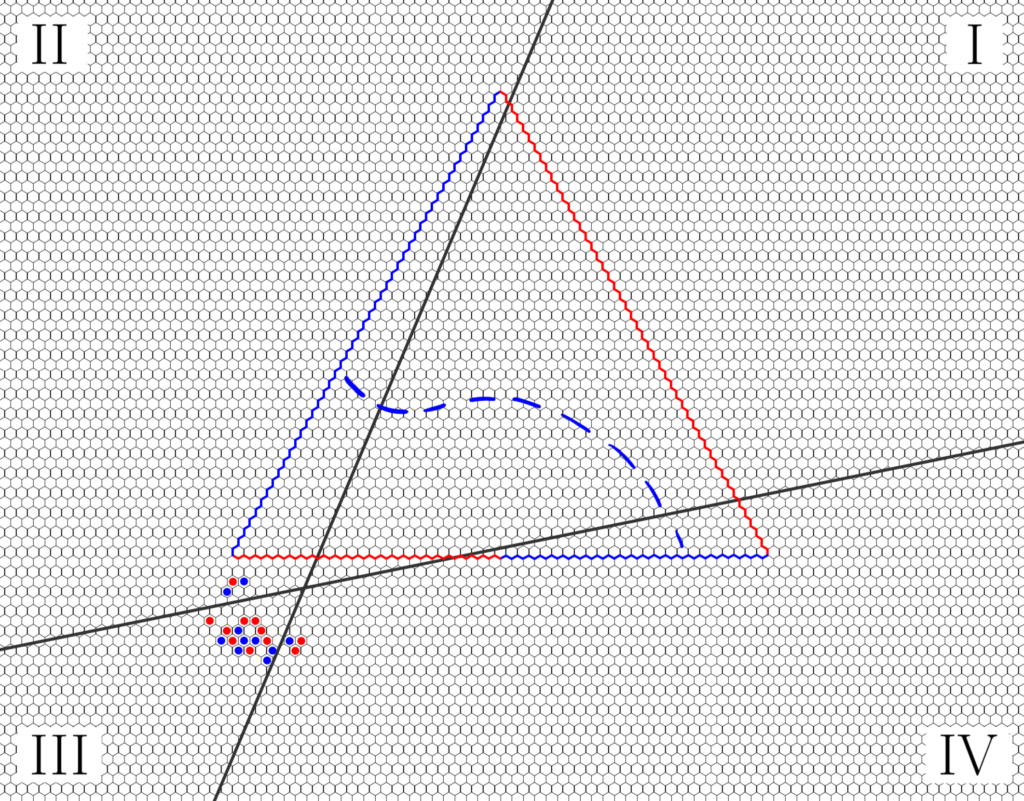
Abstract: Hex is a two-player game where the goal is to form a contiguous path of tokens from one side of a finite rectangular board to the opposite side. It is a famous classical result that Hex admits no draws: a completely filled board is a win for exactly one player. Infinite Hex is a variant introduced recently by Hamkins and Leonessi. It is played on the infinite two-dimensional grid
16 NOvember 2023 11:00 am ET
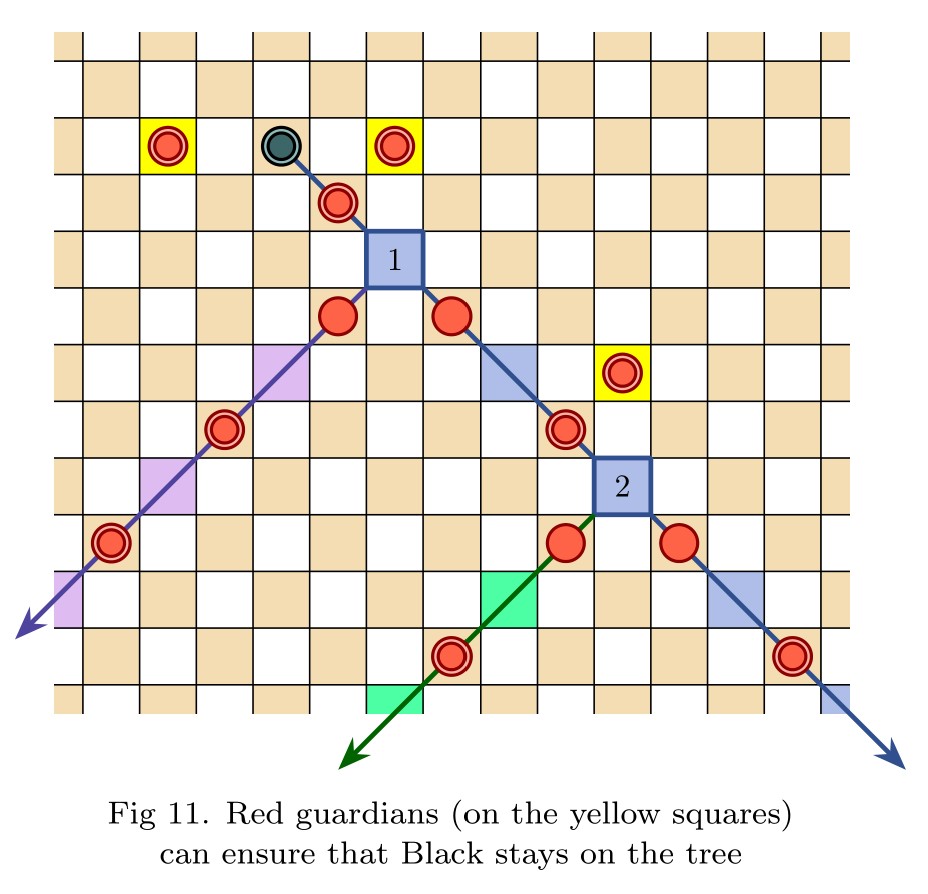
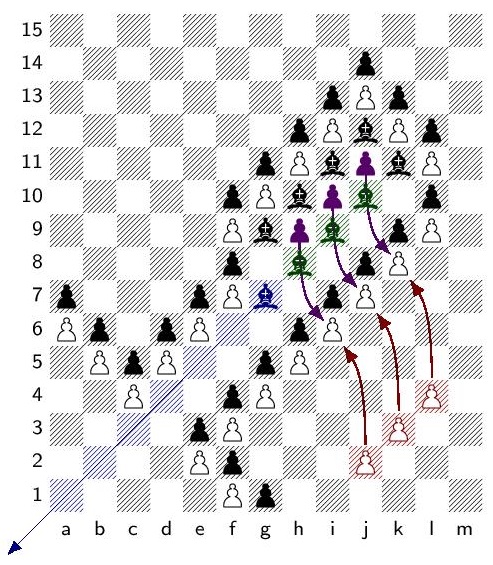
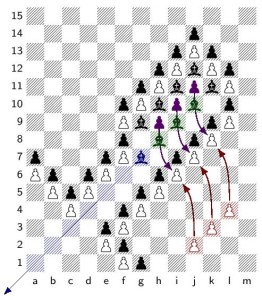
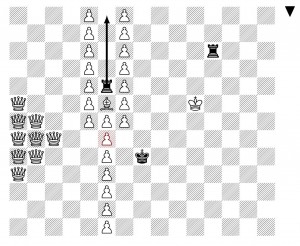
A finite position in infinite chess with game value 𝜔 2 + 𝑘
Andreas Tsevas, Physics, Ludwig Maximalians Universität München



Abstract: I present a position in infinite chess with finitely many pieces and a game value of
7 December 2023 11:00 am ET
All Countable Ordinals Arise as Game Values in Infinite Chess
Matthew Bolan, University of Toronto



Abstract: For every countable ordinal