[bibtex key=”HamkinsWoodin:The-universal-finite-set”]
Abstract. We define a certain finite set in set theory $\{x\mid\varphi(x)\}$ and prove that it exhibits a universal extension property: it can be any desired particular finite set in the right set-theoretic universe and it can become successively any desired larger finite set in top-extensions of that universe. Specifically, ZFC proves the set is finite; the definition $\varphi$ has complexity $\Sigma_2$, so that any affirmative instance of it $\varphi(x)$ is verified in any sufficiently large rank-initial segment of the universe $V_\theta$; the set is empty in any transitive model and others; and if $\varphi$ defines the set $y$ in some countable model $M$ of ZFC and $y\subseteq z$ for some finite set $z$ in $M$, then there is a top-extension of $M$ to a model $N$ in which $\varphi$ defines the new set $z$. Thus, the set shows that no model of set theory can realize a maximal $\Sigma_2$ theory with its natural number parameters, although this is possible without parameters. Using the universal finite set, we prove that the validities of top-extensional set-theoretic potentialism, the modal principles valid in the Kripke model of all countable models of set theory, each accessing its top-extensions, are precisely the assertions of S4. Furthermore, if ZFC is consistent, then there are models of ZFC realizing the top-extensional maximality principle.
Woodin had established the universal algorithm phenomenon, showing that there is a Turing machine program with a certain universal top-extension property in models of arithmetic (see also work of Blanck and Enayat 2017 and upcoming paper of mine with Gitman and Kossak; also my post The universal algorithm: a new simple proof of Woodin’s theorem). Namely, the program provably enumerates a finite set of natural numbers, but it is relatively consistent with PA that it enumerates any particular desired finite set of numbers, and furthermore, if $M$ is any model of PA in which the program enumerates the set $s$ and $t$ is any (possibly nonstandard) finite set in $M$ with $s\subseteq t$, then there is a top-extension of $M$ to a model $N$ in which the program enumerates exactly the new set $t$. So it is a universal finite computably enumerable set, which can in principle be any desired finite set of natural numbers in the right arithmetic universe and become any desired larger finite set in a suitable larger arithmetic universe.
I had inquired whether there is a set-theoretic analogue of this phenomenon, using $\Sigma_2$ definitions in set theory in place of computable enumerability (see The universal definition — it can define any mathematical object you like, in the right set-theoretic universe). The idea was that just as a computably enumerable set is one whose elements are gradually revealed as the computation proceeds, a $\Sigma_2$-definable set in set theory is precisely one whose elements become verified at some level $V_\theta$ of the cumulative set-theoretic hierarchy as it grows. In this sense, $\Sigma_2$ definability in set theory is analogous to computable enumerability in arithmetic.
Main Question. Is there a universal $\Sigma_2$ definition in set theory, one which can define any desired particular set in some model of \ZFC\ and always any desired further set in a suitable top-extension?
I had noticed in my earlier post that one can do this using a $\Pi_3$ definition, or with a $\Sigma_2$ definition, if one restricts to models of a certain theory, such as $V\neq\text{HOD}$ or the eventual GCH, or if one allows $\{x\mid\varphi(x)\}$ sometimes to be a proper class.
Here, we provide a fully general affirmative answer with the following theorem.
Main Theorem. There is a formula $\varphi(x)$ of complexity $\Sigma_2$ in the language of set theory, provided in the proof, with the following properties:
- ZFC proves that $\{x\mid \varphi(x)\}$ is a finite set.
- In any transitive model of \ZFC\ and others, this set is empty.
- If $M$ is a countable model of ZFC in which $\varphi$ defines the set $y$ and $z\in M$ is any finite set in $M$ with $y\subseteq z$, then there is a top-extension of $M$ to a model $N$ in which $\varphi$ defines exactly $z$.
By taking the union of the set defined by $\varphi$, an arbitrary set can be achieved; so the finite-set result as stated in the main theorem implies the arbitrary set case as in the main question. One can also easily deduce a version of the theorem to give a universal countable set or a universal set of some other size (for example, just take the union of the countable elements of the universal set). One can equivalently formulate the main theorem in terms of finite sequences, rather than sets, so that the sequence is extended as desired in the top-extension. The sets $y$ and $z$ in statement (3) may be nonstandard finite, if $M$ if $\omega$-nonstandard.
We use this theorem to establish the fundamental validities of top-extensional set-theoretic potentialism.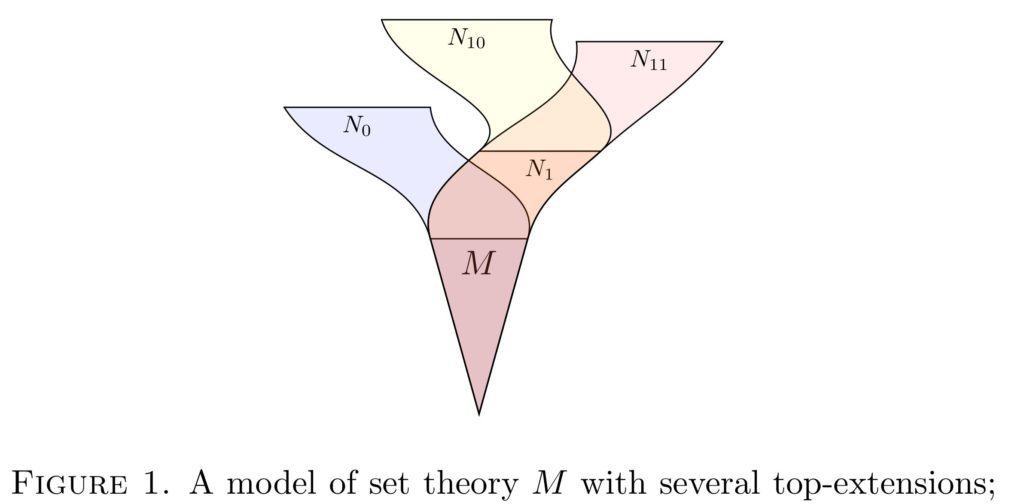 
Specifically, in the potentialist system consisting of the countable models of ZFC, with each accessing its top extensions, the modal validities with respect to substitution instances in the language of set theory, with parameters, are exactly the assertions of S4. When only sentences are considered, the validities are between S4 and S5, with both endpoints realized.
In particular, we prove that if ZFC is consistent, then there is a model $M$ of ZFC with the top-extensional maximality principle: any sentence $\sigma$ in the language of set theory which is true in some top extension $M^+$ and all further top extensions of $M^+$, is already true in $M$.
This principle is true is any model of set theory with a maximal $\Sigma_2$ theory, but it is never true when $\sigma$ is allowed to have natural-number parameters, and in particular, it is never true in any $\omega$-standard model of set theory.
Click through to the arXiv for more, the full article in pdf.
[bibtex key=”HamkinsWoodin:The-universal-finite-set”]
