I was interviewed by Sean Carroll for his Mindscape Podcast, broadcast 15 July 2024.
Puzzles of reality and infinity, Mindscape Podcast
Reply
Tag Archives: multiverse
How the continuum hypothesis could have been a fundamental axiom, UC Irvine Logic & Philosoph of Science Colloquium, March 2024
This will be a talk for the Logic and Philosophy of Science Colloquium at the University of California at Irvine, 15 March 2024.
Abstract. With a simple historical thought experiment, I should like to describe how we might easily have come to view the continuum hypothesis as a fundamental axiom, one necessary for mathematics, indispensable even for calculus.
The paper is now available at How the continuum hypothesis could have been a fundamental axiom.
The Gödel incompleteness phenomenon, interview with Rahul Sam
Please enjoy my conversation with Rahul Sam for his podcast, a sweeping discussion of topics in the philosophy of mathematics—potentialism, pluralism, Gödel incompleteness, philosophy of set theory, large cardinals, and much more.
Pluralism in the foundations of mathematics, ASL invited address, joint APA/ASL meeting, New York, January 2024
This will be an invited ASL address at the joint meeting of the ASL with the APA Eastern Division conference, held in New York 15-18 January 2024. My talk will be 16 January 2024 11:00 am.
Abstract. I shall give an account of the debate on set-theoretic pluralism and pluralism generally in the foundations of mathematics, including arithmetic. Is there ultimately just
one mathematical universe, the final background context, in which every mathematical
question has an absolute, determinate answer? Or do we have rather a multiverse of
mathematical foundations? Some mathematicians and philosophers favor a hybrid notion, with pluralism at the higher realms of set theory, but absoluteness for arithmetic.
What grounds are there for these various positions? How are we to adjudicate between
them? What ultimately is the purpose of a foundation of mathematics?
See the related paper on the mathematical thought experiment: How the continuum hypothesis could have been a fundamental axiom.
Paradox, Infinity, & The Foundations of Mathematics, interview with Robinson Erhardt, January 2023
This was an interview with Robinson Erhardt on Robinson’s Podcast, part of his series of interviews with various philosophers, including many philosophers of mathematics and more.
We had a wonderfully wide-ranging discussion about the philosophy of mathematics, the philosophy of set theory, pluralism, and many other topics. The main focus was the topic of infinity, following selections from my new book, The Book of Infinity, currently being serialized on my substack, joeldavidhamkins.substack.com, with discussion of Zeno’s paradox, the Chocolatier’s Game, Hilbert’s Grand Hotel and more.
Robinson compiled the following outline with links to special parts of the interview:
- 00:00 Introduction
- 2:52 Is Joel a Mathematician or a Philosopher?
- 6:13 The Philosophical Influence of Hugh Woodin
- 10:29 The Intersection of Set Theory and Philosophy of Math
- 16:29 Serializing the Book of the Infinite
- 20:05 Zeno of Elea, Continuity, and Geometric Series
- 39:39 Infinite Games and the Chocolatier
- 53:35 Hilbert’s Hotel
- 1:10:26 Cantor’s Theorem
- 1:31:37 The Continuum Hypothesis
- 1:43:02 The Set-Theoretic Multiverse
- 2:00:25 Berry’s Paradox and Large Numbers
- 2:16:15 Skolem’s Paradox and Indescribable Numbers
- 2:28:41 Pascal’s Wager and Reasoning Around Remote Events
- 2:49:35 MathOverflow
- 3:04:40 Joel’s Impeccable Fashion Sense
Read the book here: joeldavidhamkins.substack.com.
Pseudo-countable models
[bibtex key=”Hamkins:Pseudo-countable-models”]
Download pdf at arXiv:2210.04838
Abstract. Every mathematical structure has an elementary extension to a pseudo-countable structure, one that is seen as countable inside a suitable class model of set theory, even though it may actually be uncountable. This observation, proved easily with the Boolean ultrapower theorem, enables a sweeping generalization of results concerning countable models to a rich realm of uncountable models. The Barwise extension theorem, for example, holds amongst the pseudo-countable models—every pseudo-countable model of ZF admits an end extension to a model of ZFC+V=L. Indeed, the class of pseudo-countable models is a rich multiverse of set-theoretic worlds, containing elementary extensions of any given model of set theory and closed under forcing extensions and interpreted models, while simultaneously fulfilling the Barwise extension theorem, the Keisler-Morley theorem, the resurrection theorem, and the universal finite sequence theorem, among others.
Workshop on the Set-theoretic Multiverse, Konstanz, September 2022
Masterclass of “The set-theoretic multiverse” ten years after
Focused on mathematical and philosophical aspects of the set-theoretic multiverse and the pluralist debate in the philosophy of set theory, this workshop will have a master class on potentialism, a series of several speakers, and a panel discussion. To be held 21-22 September 2022 at the University of Konstanz, Germany. (Contact organizers for Zoom access.)
I shall make several contributions to the meeting.
Master class tutorial on potentialism
I shall give a master class tutorial on potentialism, an introduction to the general theory of potentialism that has been emerging in recent work, often developed as a part of research on set-theoretic pluralism, but just as often branching out to a broader application. Although the debate between potentialism and actualism in the philosophy of mathematics goes back to Aristotle, recent work divorces the potentialist idea from its connection with infinity and undertakes a more general analysis of possible mathematical universes of any kind. Any collection of mathematical structures forms a potentialist system when equipped with an accessibility relation (refining the submodel relation), and one can define the modal operators of possibility $\Diamond\varphi$, true at a world when $\varphi$ is true in some larger world, and necessity $\Box\varphi$, true in a world when $\varphi$ is true in all larger worlds. The project is to understand the structures more deeply by understanding their modal nature in the context of a potentialist system. The rise of modal model theory investigates very general instances of potentialist system, for sets, graphs, fields, and so on. Potentialism for the models of arithmetic often connects with deeply philosophical ideas on ultrafinitism. And the spectrum of potentialist systems for the models of set theory reveals fundamentally different conceptions of set-theoretic pluralism and possibility.
The multiverse view on the axiom of constructibility
I shall give a talk on the multiverse perspective on the axiom of constructibility. Set theorists often look down upon the axiom of constructibility V=L as limiting, in light of the fact that all the stronger large cardinals are inconsistent with this axiom, and furthermore the axiom expresses a minimizing property, since $L$ is the smallest model of ZFC with its ordinals. Such views, I argue, stem from a conception of the ordinals as absolutely completed. A potentialist conception of the set-theoretic universe reveals a sense in which every set-theoretic universe might be extended (in part upward) to a model of V=L. In light of such a perspective, the limiting nature of the axiom of constructibility tends to fall away.
Panel discussion: The multiverse view—challenges for the next ten years
This will be a panel discussion on the set-theoretic multiverse, with panelists including myself, Carolin Antos-Kuby, Giorgio Venturi, and perhaps others.
The ontology of mathematics, Japan Association for the Philosophy of Science, June 2022
I shall give the Invited Lecture for the Annual Meeting (online) of the Japanese Association for the Philosophy of Science, 18-19 June 2022.
Abstract. What is the nature of mathematical ontology—what does it mean to make existence assertions in mathematics? Is there an ideal mathematical realm, a mathematical universe, that those assertions are about? Perhaps there is more than one. Does every mathematical assertion ultimately have a definitive truth value? I shall lay out some of the back-and-forth in what is currently a vigorous debate taking place in the philosophy of set theory concerning pluralism in the set-theoretic foundations, concerning whether there is just one set-theoretic universe underlying our mathematical claims or whether there is a diversity of possible set-theoretic conceptions.
Pluralism in the ontology of mathematics, MaMuPhi, Paris, February 2022
This will be a talk for the conference L’indépendance mathématique et ses limites logiques, an instance of the MAMUPHI seminar (mathématiques – musique – philosophie), organized by Mirna Džamonja, 12 February 2022. Most talks will be in-person in Paris, but my talk will be on Zoom via https://u-pec-fr.zoom.us/j/86448599486 at 4:30 pm CET (10:30 am EST).
Abstract: What is the nature of mathematical ontology—what does it mean to make existence assertions in mathematics? Is there an ideal mathematical realm, a mathematical universe, that those assertions are about? Perhaps there is more than one. Does every mathematical assertion ultimately have a definitive truth value? I shall lay out some of the back-and-forth in what is currently a vigorous debate taking place in the philosophy of set theory concerning pluralism in the set-theoretic foundations, concerning whether there is just one set-theoretic universe underlying our mathematical claims or whether there is a diversity of possible set-theoretic conceptions.
Is there just one mathematical universe? DRIFT, Amsterdam, May 2019
This will be a talk for the Wijsgerig Festival DRIFT 2019, held in Amsterdam May 11, 2019. The theme of the conference is: Ontology.
Abstract. What does it mean to make existence assertions in mathematics?
Is there a mathematical universe, perhaps an ideal mathematical reality, that the assertions are about? Is there possibly more than one such universe? Does every mathematical assertion ultimately have a definitive truth value? I shall lay out some of the back-and-forth in what is currently a vigorous debate taking place in the philosophy of set theory concerning pluralism in the set-theoretic foundations, concerning whether there is just one set-theoretic universe underlying our mathematical claims or whether there is a diversity of possible set-theoretic worlds.
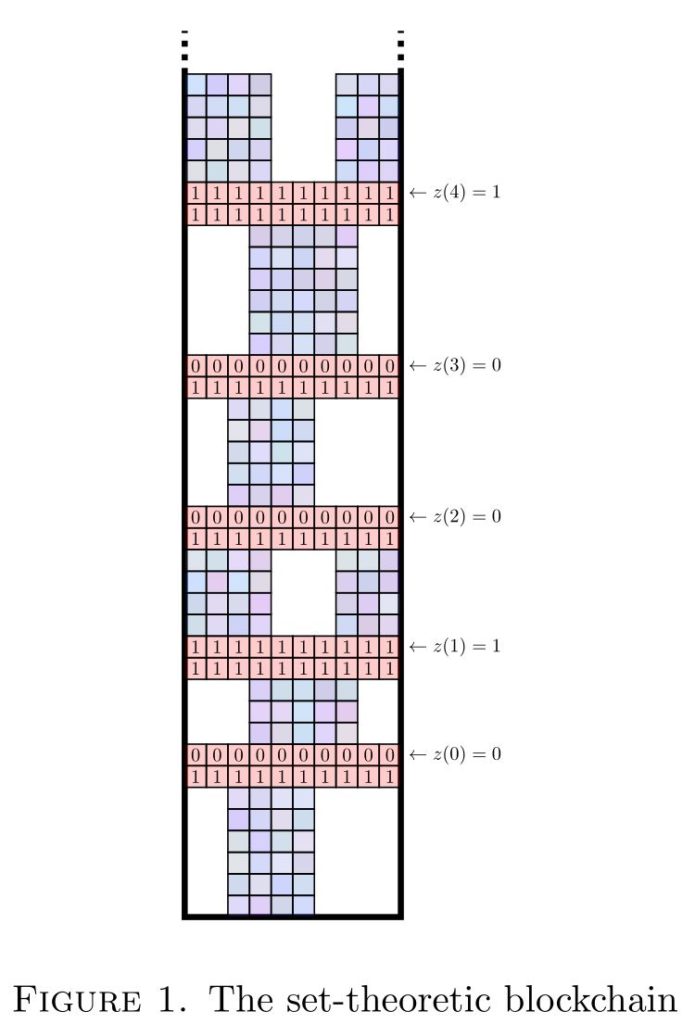
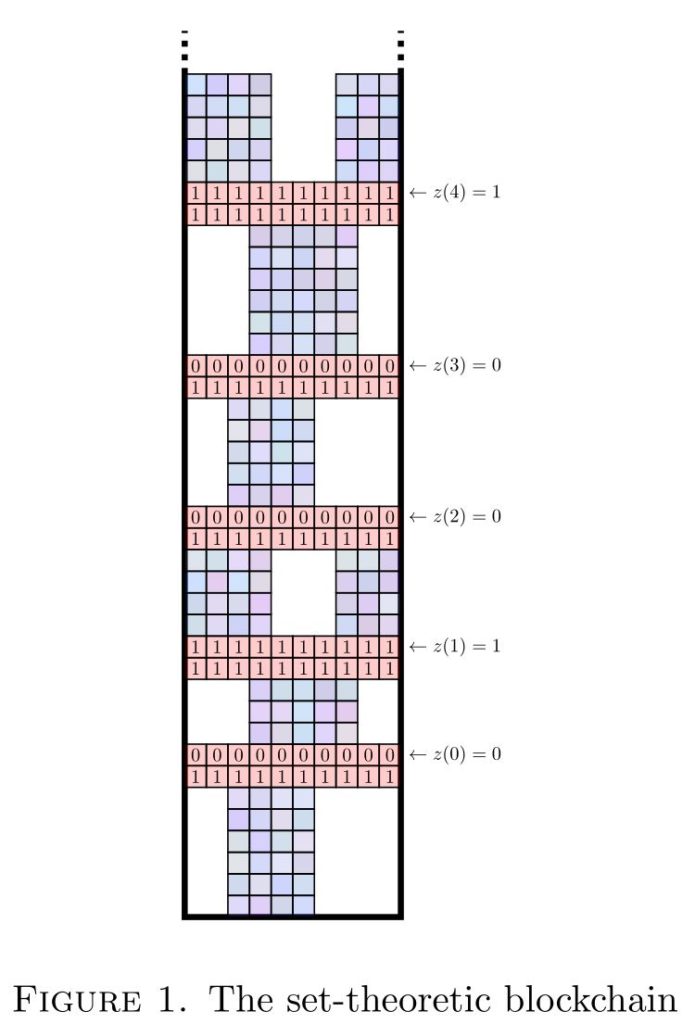
Set-theoretic blockchains
[bibtex key=”HabicHamkinsKlausnerVernerWilliams2018:Set-theoretic-blockchains”]
Abstract. Given a countable model of set theory, we study the structure of its generic multiverse, the collection of its forcing extensions and ground models, ordered by inclusion. Mostowski showed that any finite poset embeds into the generic multiverse while preserving the nonexistence of upper bounds. We obtain several improvements of his result, using what we call the blockchain construction to build generic objects with varying degrees of mutual genericity. The method accommodates certain infinite posets, and we can realize these embeddings via a wide variety of forcing notions, while providing control over lower bounds as well. We also give a generalization to class forcing in the context of second-order set theory, and exhibit some further structure in the generic multiverse, such as the existence of exact pairs.
Nonamalgamation in the Cohen generic multiverse, CUNY Logic Workshop, March 2018
This will be a talk for the CUNY Logic Workshop on March 23, 2018, GC 6417 2-3:30pm.
Abstract. Consider a countable model of set theory $M$ in the context of all its successive forcing extensions and grounds. This generic multiverse has long been known to exhibit instances of nonamalgamation: one can have two extensions $M[c]$ and $M[d]$, both adding a merely a generic Cohen real, which have no further extension in common. In this talk, I shall describe new joint work that illuminates the extent of non-amalgamation: every finite partial order (and more) embeds into the generic multiverse over any given model in a way that preserves amalgamability and non-amalgamability. The proof uses the set-theoretic blockchain argument (pictured above), which has affinities with constructions in computability theory in the Turing degrees. Other arguments, which also resemble counterparts in computability theory, show that the generic multiverse exhibits the exact pair phenonemon for increasing chains. This is joint work with Miha Habič, myself, Lukas Daniel Klausner and Jonathan Verner. The paper will be available this Spring.
- Upward countable closure in the generic multiverse of forcing to add a Cohen real
- Upward closure and amalgamation in the generic multiverse of a countable model of set theory
- Upward closure in the generic multiverse of a countable model of set theory, RIMS 2015, Kyoto, Japan
- Upward closure in the toy multiverse of all countable models of set theory
https://plus.google.com/u/0/+JoelDavidHamkins1/posts/NJp2N7bkkrR
The modal logic of set-theoretic potentialism and the potentialist maximality principles
Joint work with Øystein Linnebo, University of Oslo.
[bibtex key=”HamkinsLinnebo:Modal-logic-of-set-theoretic-potentialism”]
Abstract. We analyze the precise modal commitments of several natural varieties of set-theoretic potentialism, using tools we develop for a general model-theoretic account of potentialism, building on those of Hamkins, Leibman and Löwe (Structural connections between a forcing class and its modal logic), including the use of buttons, switches, dials and ratchets. Among the potentialist conceptions we consider are: rank potentialism (true in all larger $V_\beta$); Grothendieck-Zermelo potentialism (true in all larger $V_\kappa$ for inaccessible cardinals $\kappa$); transitive-set potentialism (true in all larger transitive sets); forcing potentialism (true in all forcing extensions); countable-transitive-model potentialism (true in all larger countable transitive models of ZFC); countable-model potentialism (true in all larger countable models of ZFC); and others. In each case, we identify lower bounds for the modal validities, which are generally either S4.2 or S4.3, and an upper bound of S5, proving in each case that these bounds are optimal. The validity of S5 in a world is a potentialist maximality principle, an interesting set-theoretic principle of its own. The results can be viewed as providing an analysis of the modal commitments of the various set-theoretic multiverse conceptions corresponding to each potentialist account.
Set-theoretic potentialism is the view in the philosophy of mathematics that the universe of set theory is never fully completed, but rather unfolds gradually as parts of it increasingly come into existence or become accessible to us. On this view, the outer reaches of the set-theoretic universe have merely potential rather than actual existence, in the sense that one can imagine “forming” or discovering always more sets from that realm, as many as desired, but the task is never completed. For example, height potentialism is the view that the universe is never fully completed with respect to height: new ordinals come into existence as the known part of the universe grows ever taller. Width potentialism holds that the universe may grow outwards, as with forcing, so that already existing sets can potentially gain new subsets in a larger universe. One commonly held view amongst set theorists is height potentialism combined with width actualism, whereby the universe grows only upward rather than outward, and so at any moment the part of the universe currently known to us is a rank initial segment $V_\alpha$ of the potential yet-to-be-revealed higher parts of the universe. Such a perspective might even be attractive to a Platonistically inclined large-cardinal set theorist, who wants to hold that there are many large cardinals, but who also is willing at any moment to upgrade to a taller universe with even larger large cardinals than had previously been mentioned. Meanwhile, the width-potentialist height-actualist view may be attractive for those who wish to hold a potentialist account of forcing over the set-theoretic universe $V$. On the height-and-width-potentialist view, one views the universe as growing with respect to both height and width. A set-theoretic monist, in contrast, with an ontology having only a single fully existing universe, will be an actualist with respect to both width and height. The second author has described various potentialist views in previous work.
Although we are motivated by the case of set-theoretic potentialism, the potentialist idea itself is far more general, and can be carried out in a general model-theoretic context. For example, the potentialist account of arithmetic is deeply connected with the classical debates surrounding potential as opposed to actual infinity, and indeed, perhaps it is in those classical debates where one finds the origin of potentialism. More generally, one can provide a potentialist account of truth in the context of essentially any kind of structure in any language or theory.
Our project here is to analyze and understand more precisely the modal commitments of various set-theoretic potentialist views. After developing a general model-theoretic account of the semantics of potentialism and providing tools for establishing both lower and upper bounds on the modal validities for various kinds of potentialist contexts, we shall use those tools to settle exactly the propositional modal validities for several natural kinds of set-theoretic height and width potentialism.
Here is a summary account of the modal logics for various flavors of set-theoretic potentialism.
In each case, the indicated lower and upper bounds are realized in particular worlds, usually in the strongest possible way that is consistent with the stated inclusions, although in some cases, this is proved only under additional mild technical hypotheses. Indeed, some of the potentialist accounts are only undertaken with additional set-theoretic assumptions going beyond ZFC. For example, the Grothendieck-Zermelo account of potentialism is interesting mainly only under the assumption that there are a proper class of inaccessible cardinals, and countable-transitive-model potentialism is more robust under the assumption that every real is an element of a countable transitive model of set theory, which can be thought of as a mild large-cardinal assumption.
The upper bound of S5, when it is realized, constitutes a potentialist maximality principle, for in such a case, any statement that could possibly become actually true in such a way that it remains actually true as the universe unfolds, is already actually true. We identify necessary and sufficient conditions for each of the concepts of potentialism for a world to fulfill this potentialist maximality principle. For example, in rank-potentialism, a world $V_\kappa$ satisfies S5 with respect to the language of set theory with arbitrary parameters if and only if $\kappa$ is $\Sigma_3$-correct. And it satisfies S5 with respect to the potentialist language of set theory with parameters if and only if it is $\Sigma_n$-correct for every $n$. Similar results hold for each of the potentialist concepts.
Finally, let me mention the strong affinities between set-theoretic potentialism and set-theoretic pluralism, particularly with the various set-theoretic multiverse conceptions currently in the literature. Potentialists may regard themselves mainly as providing an account of truth ultimately for a single universe, gradually revealed, the limit of their potentialist system. Nevertheless, the universe fragments of their potentialist account can often naturally be taken as universes in their own right, connected by the potentialist modalities, and in this way, every potentialist system can be viewed as a multiverse. Indeed, the potentialist systems we analyze in this article—including rank potentialism, forcing potentialism, generic-multiverse potentialism, countable-transitive-model potentialism, countable-model potentialism—each align with corresponding natural multiverse conceptions. Because of this, we take the results of this article as providing not only an analysis of the modal commitments of set-theoretic potentialism, but also an analysis of the modal commitments of various particular set-theoretic multiverse conceptions. Indeed, one might say that it is possible (ahem), in another world, for this article to have been entitled, “The modal logic of various set-theoretic multiverse conceptions.”
For more, please follow the link to the arxiv where you can find the full article.
[bibtex key=”HamkinsLinnebo:Modal-logic-of-set-theoretic-potentialism”]
Upward closure and amalgamation in the generic multiverse of a countable model of set theory
[bibtex key=Hamkins2016:UpwardClosureAndAmalgamationInTheGenericMultiverse]
Abstract. I prove several theorems concerning upward closure and amalgamation in the generic multiverse of a countable transitive model of set theory. Every such model $W$ has forcing extensions $W[c]$ and $W[d]$ by adding a Cohen real, which cannot be amalgamated in any further extension, but some nontrivial forcing notions have all their extensions amalgamable. An increasing chain $W[G_0]\subseteq W[G_1]\subseteq\cdots$ has an upper bound $W[H]$ if and only if the forcing had uniformly bounded essential size in $W$. Every chain $W\subseteq W[c_0]\subseteq W[c_1]\subseteq \cdots$ of extensions adding Cohen reals is bounded above by $W[d]$ for some $W$-generic Cohen real $d$.
This article is based upon I talk I gave at the conference on Recent Developments in Axiomatic Set Theory at the Research Institute for Mathematical Sciences (RIMS) at Kyoto University, Japan in September, 2015, and I am extremely grateful to my Japanese hosts, especially Toshimichi Usuba, for supporting my research visit there and also at the CTFM conference at Tokyo Institute of Technology just preceding it. This article includes material adapted from section section 2 of Set-theoretic geology, joint with G. Fuchs, myself and J. Reitz, and also includes a theorem that was proved in a series of conversations I had with Giorgio Venturi at the Young Set Theory Workshop 2011 in Bonn and continuing at the London 2011 summer school on set theory at Birkbeck University London.
- My talk at RIMS: Upward closure in the generic multiverse of a countable model of set theory
- My talk at CTFM: Universality and embeddability amongst the models of set theory
- G. Fuchs, J. D. Hamkins, J. Reitz, Set-theoretic geology, Annals of Pure and Applied Logic, vol. 166, iss. 4, pp. 464-501, 2015.
- Upward closure in the toy multiverse of all countable models of set theory
- Upward countable closure in the generic multiverse of forcing to add a Cohen real
Being HOD-of-a-set is invariant throughout the generic multiverse
$\newcommand\HOD{\text{HOD}}$The axiom $V=\HOD$, introduced by Gödel, asserts that every set is ordinal definable. This axiom has a subtler foundational aspect than might at first be expected. The reason is that the general concept of “object $x$ is definable using parameter $p$” is not in general first-order expressible in set theory; it is of course a second-order property, which makes sense only relative to a truth predicate, and by Tarski’s theorem, we can have no first-order definable truth predicate. Thus, the phrase “definable using ordinal parameters” is not directly meaningful in the first-order language of set theory without further qualification or explanation. Fortunately, however, it is a remarkable fact that when we allow definitions to use arbitrary ordinal parameters, as we do with $\HOD$, then we can in fact make such qualifications in such a way that the axiom becomes first-order expressible in set theory. Specifically, we say officially that $V=\HOD$ holds, if for every set $x$, there is an ordinal $\theta$ with $x\in V_\theta$, for which which $x$ is definable by some formula $\psi(x)$ in the structure $\langle V_\theta,{\in}\rangle$ using ordinal parameters. Since $V_\theta$ is a set, we may freely make reference to first-order truth in $V_\theta$ without requiring any truth predicate in $V$. Certainly any such $x$ as this is also ordinal-definable in $V$, since we may use $\theta$ and the Gödel-code of $\psi$ also as parameters, and note that $x$ is the unique object such that it is in $V_\theta$ and satisfies $\psi$ in $V_\theta$. (Note that inside an $\omega$-nonstandard model of set theory, we may really need to use $\psi$ as a parameter, since it may be nonstandard, and $x$ may not be definable in $V_\theta$ using a meta-theoretically standard natural number; but fortunately, the Gödel code of a formula is an integer, which is still an ordinal, and this issue is the key to the issue.) Conversely, if $x$ is definable in $V$ using formula $\varphi(x,\vec\alpha)$ with ordinal parameters $\vec\alpha$, then it follows by the reflection theorem that $x$ is defined by $\varphi(x,\vec\alpha)$ inside some $V_\theta$. So this formulation of $V=HOD$ is expressible and exactly captures the desired second-order property that every set is ordinal-definable.
Consider next the axiom $V=\HOD(b)$, asserting that every set is definable from ordinal parameters and parameter $b$. Officially, as before, $V=\HOD(b)$ asserts that for every $x$, there is an ordinal $\theta$, formula $\psi$ and ordinals $\vec \alpha<\theta$, such that $x$ is the unique object in $V_\theta$ for which $\langle V_\theta,{\in}\rangle\models\psi(x,\vec\alpha,b)$, and the reflection argument shows again that this way of defining the axiom exactly captures the intended idea.
The axiom I actually want to focus on is $\exists b\,\left( V=\HOD(b)\right)$, asserting that the universe is $\HOD$ of a set. (I assume ZFC in the background theory.) It turns out that this axiom is constant throughout the generic multiverse.
Theorem. The assertion $\exists b\, (V=\HOD(b))$ is forcing invariant.
- If it holds in $V$, then it continues to hold in every set forcing extension of $V$.
- If it holds in $V$, then it holds in every ground of $V$.
Thus, the truth of this axiom is invariant throughout the generic multiverse.
Proof. Suppose that $\text{ZFC}+V=\HOD(b)$, and $V[G]$ is a forcing extension of $V$ by generic filter $G\subset\mathbb{P}\in V$. By the ground-model definability theorem, it follows that $V$ is definable in $V[G]$ from parameter $P(\mathbb{P})^V$. Thus, using this parameter, as well as $b$ and additional ordinal parameters, we can define in $V[G]$ any particular object in $V$. Since this includes all the $\mathbb{P}$-names used to form $V[G]$, it follows that $V[G]=\HOD(b,P(\mathbb{P})^V,G)$, and so $V[G]$ is $\HOD$ of a set, as desired.
Conversely, suppose that $W$ is a ground of $V$, so that $V=W[G]$ for some $W$-generic filter $G\subset\mathbb{P}\in W$, and $V=\HOD(b)$ for some set $b$. Let $\dot b$ be a name for which $\dot b_G=b$. Every object $x\in W$ is definable in $W[G]$ from $b$ and ordinal parameters $\vec\alpha$, so there is some formula $\psi$ for which $x$ is unique such that $\psi(x,b,\vec\alpha)$. Thus, there is some condition $p\in\mathbb{P}$ such that $x$ is unique such that $p\Vdash\psi(\check x,\dot b,\check{\vec\alpha})$. If $\langle p_\beta\mid\beta<|\mathbb{P}|\rangle$ is a fixed enumeration of $\mathbb{P}$ in $W$, then $p=p_\beta$ for some ordinal $\beta$, and we may therefore define $x$ in $W$ using ordinal parameters, along with $\dot b$ and the fixed enumeration of $\mathbb{P}$. So $W$ thinks the universe is $\HOD$ of a set, as desired.
Since the generic multiverse is obtained by iteratively moving to forcing extensions to grounds, and each such movement preserves the axiom, it follows that $\exists b\, (V=\HOD(b))$ is constant throughout the generic multiverse. QED
Theorem. If $V=\HOD(b)$, then there is a forcing extension $V[G]$ in which $V=\HOD$ holds.
Proof. We are working in ZFC. Suppose that $V=\HOD(b)$. We may assume $b$ is a set of ordinals, since such sets can code any given set. Consider the following forcing iteration: first add a Cohen real $c$, and then perform forcing $G$ that codes $c$, $P(\omega)^V$ and $b$ into the GCH pattern at uncountable cardinals, and then perform self-encoding forcing $H$ above that coding, coding also $G$ (see my paper on Set-theoretic geology for further details on self-encoding forcing). In the final model $V[c][G][H]$, therefore, the objects $c$, $b$, $P(\omega)^V$, $G$ and $H$ are all definable without parameters. Since $V\subset V[c][G][H]$ has a closure point at $\omega$, it satisfies the $\omega_1$-approximation and cover properties, and therefore the class $V$ is definable in $V[c][G][H]$ using $P(\omega)^V$ as a parameter. Since this parameter is itself definable without parameters, it follows that $V$ is parameter-free definable in $V[c][G][H]$. Since $b$ is also definable there, it follows that every element of $\HOD(b)^V=V$ is ordinal-definable in $V[c][G][H]$. And since $c$, $G$ and $H$ are also definable without parameters, we have $V[c][G][H]\models V=\HOD$, as desired. QED
Corollary. The following are equivalent.
- The universe is $\HOD$ of a set: $\exists b\, (V=\HOD(b))$.
- Somewhere in the generic multiverse, the universe is $\HOD$ of a set.
- Somewhere in the generic multiverse, the axiom $V=\HOD$ holds.
- The axiom $V=\HOD$ is forceable.
Proof. This is an immediate consequence of the previous theorems. $1\to 4\to 3\to 2\to 1$. QED
Corollary. The axiom $V=\HOD$, if true, even if true anywhere in the generic multiverse, is a switch.
Proof. A switch is a statement such that both it and its negation are necessarily possible by forcing; that is, in every set forcing extension, one can force the statement to be true and also force it to be false. We can always force $V=\HOD$ to fail, simply by adding a Cohen real. If $V=\HOD$ is true, then by the first theorem, every forcing extension has $V=\HOD(b)$ for some $b$, in which case $V=\HOD$ remains forceable, by the second theorem. QED