[bibtex key=”EnayatHamkinsWcislo2021:Topological-models-of-arithmetic”]
Abstract. Ali Enayat had asked whether there is a nonstandard model of Peano arithmetic (PA) that can be represented as , where and are continuous functions on the rationals . We prove, affirmatively, that indeed every countable model of PA has such a continuous presentation on the rationals. More generally, we investigate the topological spaces that arise as such topological models of arithmetic. The reals , the reals in any finite dimension , the long line and the Cantor space do not, and neither does any Suslin line; many other spaces do; the status of the Baire space is open.
The first author had inquired whether a nonstandard model of arithmetic could be continuously presented on the rational numbers.
Main Question. (Enayat, 2009) Are there continuous functions and on the rational numbers , such that is a nonstandard model of arithmetic?
By a model of arithmetic, what we mean here is a model of the first-order Peano axioms PA, although we also consider various weakenings of this theory. The theory PA asserts of a structure that it is the non-negative part of a discretely ordered ring, plus the induction principle for assertions in the language of arithmetic. The natural numbers , for example, form what is known as the standard model of PA, but there are also many nonstandard models, including continuum many non-isomorphic countable models.
We answer the question affirmatively, and indeed, the main theorem shows that every countable model of PA is continuously presented on . We define generally that a topological model of arithmetic is a topological space equipped with continuous functions and , for which satisfies the desired arithmetic theory. In such a case, we shall say that the underlying space continuously supports a model of arithmetic and that the model is continuously presented upon the space .
Question. Which topological spaces support a topological model of arithmetic?
In the paper, we prove that the reals , the reals in any finite dimension , the long line and Cantor space do not support a topological model of arithmetic, and neither does any Suslin line. Meanwhile, there are many other spaces that do support topological models, including many uncountable subspaces of the plane . It remains an open question whether any uncountable Polish space, including the Baire space, can support a topological model of arithmetic.
Let me state the main theorem and briefly sketch the proof.
Main Theorem. Every countable model of PA has a continuous presentation on the rationals .
Proof. We shall prove the theorem first for the standard model of arithmetic . Every school child knows that when computing integer sums and products by the usual algorithms, the final digits of the result or are completely determined by the corresponding final digits of the inputs and . Presented with only final segments of the input, the child can nevertheless proceed to compute the corresponding final segments of the output.
This phenomenon amounts exactly to the continuity of addition and multiplication with respect to what we call the final-digits topology on , which is the topology having basic open sets , the set of numbers whose binary representations ends with the digits , for any finite binary string . (One can do a similar thing with any base.) In the notation, we include the number that would arise by deleting initial s from ; for example, . Addition and multiplication are continuous in this topology, because if or has final digits , then by the school-child’s observation, this is ensured by corresponding final digits in and , and so has an open neighborhood in the final-digits product space, whose image under the sum or product, respectively, is contained in .
Let us make several elementary observations about the topology. The sets do indeed form the basis of a topology, because is empty, if and disagree on some digit (comparing from the right), or else it is either or , depending on which sequence is longer. The topology is Hausdorff, because different numbers are distinguished by sufficiently long segments of final digits. There are no isolated points, because every basic open set has infinitely many elements. Every basic open set is clopen, since the complement of is the union of , where conflicts on some digit with . The topology is actually the same as the metric topology generated by the -adic valuation, which assigns the distance between two numbers as , when is largest such that divides their difference; the set is an open ball in this metric, centered at the number represented by . (One can also see that it is metric by the Urysohn metrization theorem, since it is a Hausdorff space with a countable clopen basis, and therefore regular.) By a theorem of Sierpinski, every countable metric space without isolated points is homeomorphic to the rational line , and so we conclude that the final-digits topology on is homeomorphic to . We’ve therefore proved that the standard model of arithmetic has a continuous presentation on , as desired.
But let us belabor the argument somewhat, since we find it interesting to notice that the final-digits topology (or equivalently, the -adic metric topology on ) is precisely the order topology of a certain definable order on , what we call the final-digits order, an endless dense linear order, which is therefore order-isomorphic and thus also homeomorphic to the rational line , as desired.
The final-digits order on the natural numbers is determined by the left-to-right order of nodes and branches in a certain presentation of the binary tree, pictured in figure 1. Each node in the tree represents a natural number via the binary sequence of digits proceeding from that node down to the root, and the final-digits order is determined from the induced left-to-right order of these nodes. As one climbs the tree, successive bits are added as leading digits of the binary representations. Since leading digits of do not affect the number represented, these nodes move neither left nor right, but proceed straight up in the tree. Leading digits of , however, branch to the right at even stages in this tree and to the left at odd stages. One easily determines any instance of the final-digits order relation for natural numbers by inspecting the right-most digit of disagreement in the binary representations of and (appending leading s if necessary), and considering whether this digit’s place is even or odd.
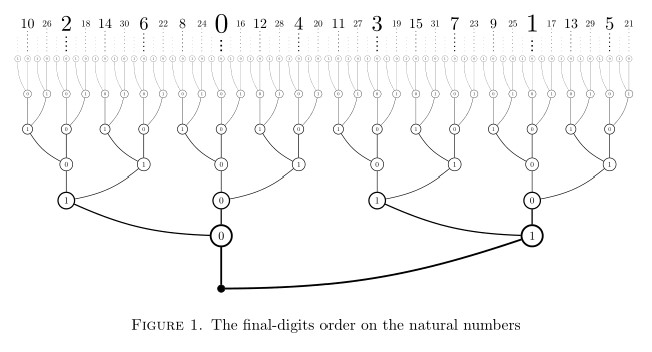
The basic open set of numbers having final digits is an open set in this order, since any number ending with is above a number with binary form and below a number with binary form in the final-digits order; so is a union of intervals in the final-digits order. Conversely, every interval in the final-digits order is open in the final-digits topology, because if , then this is determined by some final segment of the digits of (appending initial s if necessary), and so there is some containing and contained in the interval between and . Thus, the final-digits topology is the precisely same as the order topology of the final-digits order, which is a definable endless dense linear order on . Since this order is isomorphic and hence homeomorphic to the rational line , we conclude again that admits a continuous presentation on .
We now complete the proof by considering an arbitrary countable model of PA. Let be the final-digits order as defined inside . Since the reasoning of the above paragraphs can be undertaken in PA, it follows that can see that its addition and multiplication are continuous with respect to the order topology of its final-digits order. Since is countable, the final-digits order of makes it a countable endless dense linear order, which by Cantor’s theorem is therefore order-isomorphic and hence homeomorphic to . Thus, has a continuous presentation on the rational line , as desired.
The executive summary of the proof is: the arithmetic of the standard model is continuous with respect to the final-digits topology, which is the same as the -adic metric topology on , and this is homeomorphic to the rational line, because it is the order topology of the final-digits order, a definable endless dense linear order; applied in a nonstandard model , this observation means the arithmetic of is continuous with respect to its rational line , which for countable models is isomorphic to the actual rational line , and so such an is continuously presentable upon .
Let me mention the following order, which it seems many people expect to use instead of the final-digits order as we defined it above. With this order, one in effect takes missing initial digits of a number as , which is of course quite reasonable.
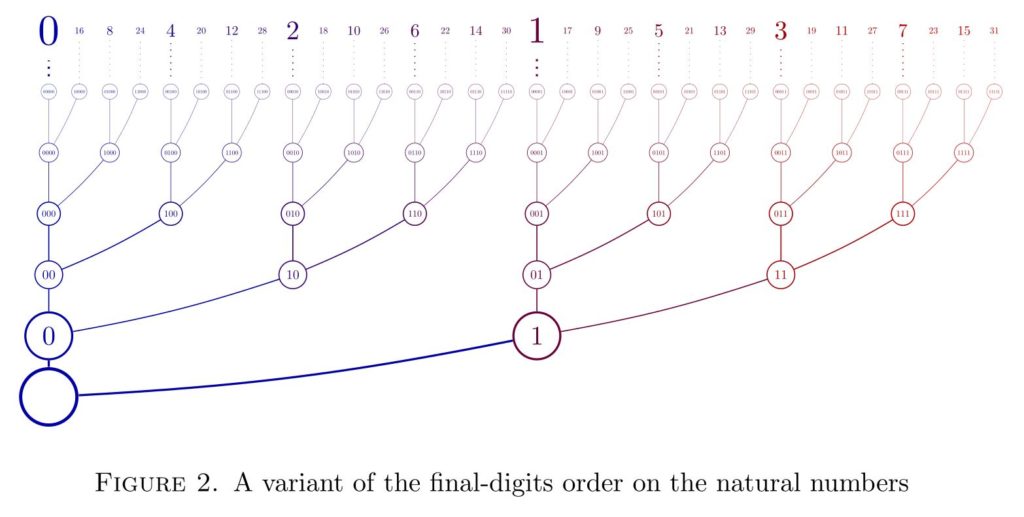
The problem with this order, however, is that the order topology is not actually the final-digits topology. For example, the set of all numbers having final digits in this order has a least element, the number , and so it is not open in the order topology. Worse, I claim that arithmetic is not continuous with respect to this order. For example, , and has an open neighborhood consisting entirely of even numbers, but every open neighborhood of has both odd and even numbers, whose sums therefore will not all be in the selected neighborhood of . Even the successor function is not continuous with respect to this order.
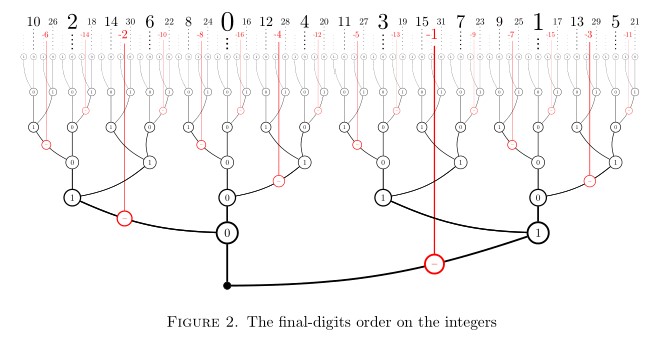
Finally, let me mention that a version of the main theorem also applies to the integers , using the following order.
Go to the article to read more.
[bibtex key=”EnayatHamkinsWcislo2018:Topological-models-of-arithmetic”]






