Quantifer elimination

Posted on July 24, 2022 by Joel David Hamkins

Nicolas Poussin, Public domain, via Wikimedia Commons

A theory admits quantifier-elimination when every assertion is logically equivalent over the theory to a quantifier-free assertion. This is quite a remarkable property when it occurs, because it reveals a severe limitation on the range of concepts that can be expressed in the theory—a quantifier-free assertion, after all, is able to express only combinations of the immediate atomic facts at hand. As a result, we are generally able to prove quantifier-elimination results for a theory only when we already have a profound understanding of it and its models, and the quantifier-elimination result itself usually leads quickly to classification of the definable objects, sets, and relations in the theory and its models. In this way, quantifier-elimination results often showcase our mastery over a particular theory and its models. So let us present a few quantifier-elimination results, exhibiting our expertise over some natural theories.

Endless dense linear orders

Consider first the theory of an endless dense linear order, such as the rational order $⟨ Q, < ⟩$ . In light of Cantor’s theorems on the universality of the rational line and the categoricity theorem for countable endless dense linear orders, we already have a fairly deep understanding of this theory and this particular model.

Consider any two rational numbers $x, y$ in the structure $⟨ Q, < ⟩$ . What can one say about them? Well, we can certainly make the atomic assertions that $x$ to a Boolean combination of these assertions.

Theorem. The theory of the rational order $⟨ Q, < ⟩$ admits elimination of quantifiers—every assertion $φ (x, \dots)$ is logically equivalent in the rational order to a quantifier-free assertion.

Proof. To see this, observe simply by Cantor’s categoricity theorem for countable dense linear orders that any pair $x < y$ in $Q$ is automorphic to any other such pair $x^{'} < y^{'}$ , and similarly for pairs with $x = y$ or $y < x$ . Consequently, $φ (x, y)$ either holds of all pairs with $x < y$ or of none of them, of all pairs with $x = y$ or none, and of all pairs with $y < x$ or none. The assertion $φ (x, y)$ is therefore equivalent to the disjunction of the three atomic relations for which it is realized, including $⊤$ as the disjunction of all three atomic possibilities and $⊥$ as the empty disjunction.

More generally, a similar observation applies to assertions $φ (x_{1}, \dots, x_{n})$ with more free variables. By Cantor’s theorem, every $n$ -tuple of points in $Q$ is automorphic with any other such $n$ -tuple of points having the same atomic order relations. Therefore any assertion holding of one such $n$ -tuple holds of all $n$ -tuples with that same atomic type, and consequently every assertion $φ (x_{1}, \dots, x_{n})$ is logically equivalent in $⟨ Q, < ⟩$ to a disjunction of those combinations of atomic relations amongst the variables $x_{1}, \dots, x_{n}$ for which it holds. In particular, every assertion is equivalent in $⟨ Q, < ⟩$ to a quantifier-free assertion. In short, the theory of this model $Th (⟨ Q, < ⟩)$ admits elimination of quantifiers.

What about other endless dense linear orders? The argument we have given so far is about the theory of this particular model $⟨ Q, < ⟩$ . In fact, the theory of the rational order is exactly the theory of endless dense linear orders, because this theory is complete, which one can see as an immediate consequence of the categoricity result of Cantor’s theorem and the downward Löwenheim-Skolem theorem. In my book, I have not yet proved the Löwenheim-Skolem theorem at this stage, however, and so let me give a direct proof of quantifier-elimination in the theory of endless dense linear orders, from which we can also derive the completeness of this theory.

Theorem. In the theory of endless dense linear orders, every statement is logically equivalent to a quantifier-free statement.

Proof. To clarify, the quantifier-free statement will have the same free variables as the original assertion, provided we allow $⊥$ and $⊤$ as logical constants. We argue by induction on formulas. The claim is of course already true for the atomic formulas, and it is clearly preserved under Boolean connectives. So it suffices inductively to eliminate the quantifier from $\exists x φ (x, \dots)$ , where $φ$ is itself quantifier-free. We can place $φ$ in disjunctive normal form, a disjunction of conjunction clauses, where each conjunction clause is a conjunction of literals, that is, atomic or negated atomic assertions. Since the atomic assertions $x < y$ , $x = y$ and $y < x$ are mutually exclusive and exhaustive, the negation of any one of them is equivalent to the disjunction of the other two. Thus we may eliminate any need for negation. By redistributing conjunction over disjunction as much as possible, we reduce to the case of $\exists x φ$ , where $φ$ is in disjunctive normal form without any negation. The existential quantifier distributes over disjunction, and so we reduce to the case $φ$ is a conjunction of atomic assertions. We may eliminate any instance of $x = x$ or $y = y$ , since these impose no requirement. We may assume that the variable $x$ occurs in each conjunct, since otherwise that conjunct commutes outside the quantifier. If $x = y$ occurs in $φ$ for some variable $y$ not identical to $x$ , then the existential claim is equivalent to $φ (y, \dots)$ , that is, by replacing every instance of $x$ with $y$ , and we have thus eliminated the quantifier. If $x < x$ occurs as one of the conjuncts, this is not satisfiable and so the assertion is equivalent to $⊥$ . Thus we have reduced to the case where $φ$ is a conjunction of assertions of the form $x < y_{i}$ and $z_{j} < x$ . If only one type of these occurs, then the assertion $\exists x φ$ is outright provable in the theory by the endless assumption and thus equivalent to $⊤$ . Otherwise, both types $x < y_{i}$ and $z_{j} < x$ occur, and in this case the existence of an $x$ obeying this conjunction of assertions is equivalent over the theory of endless dense linear orders to the quantifier-free conjunction $\underset{i, j}{⋀} z_{j} < y_{i}$ , since there will be an $x$ between them in this case and only in this case. Thus, we have eliminated the quantifier $\exists x$ , and so by induction every formula is equivalent over this theory to a quantifier-free formula.

Corollary. The theory of endless dense linear orders is complete.

Proof. If $σ$ is any sentence in this theory, then by theorem above, it is logically equivalent to a Boolean combination of quantifier-free assertions with the same variables. Since $σ$ is a sentence and there are no quantifier-free atomic sentences except $⊥$ and $⊤$ , it follows that $σ$ is equivalent over the theory to a Boolean combination of $⊥$ or $⊤$ . All such sentences are equivalent either to $⊥$ or $⊤$ , and thus either $σ$ is entailed by the theory or $\neg σ$ is, and so the theory is complete.

Corollary. In any endless dense linear order, the definable sets (allowing parameters) are precisely the finite unions of intervals.

Proof. By intervals we mean a generalized concept allowing either open or closed endpoints, as well as rays, in any of the forms:
$(a, b) [a, b] [a, b) (a, b] (a, \infty) [a, \infty) (- \infty, b) (- \infty, b]$
Of course any such interval is definable, since $(a, b)$ is defined by $(a < x) \land (x < b)$ , taking the endpoints $a$ and $b$ as parameters, and $(- \infty, b]$ is defined by $(x < b) \lor (x = b)$ , and so on. Thus, finite unions of intervals are also definable by taking a disjunction.

Conversely, any putative definition $φ (x, y_{1}, \dots, y_{n})$ is equivalent to a Boolean combination of atomic assertions concerning $x$ and the parameters $y_{i}$ . Thus, whenever it is true for some $x$ between, above, or below the parameters $y_{i}$ , it will be true of all $x$ in that same interval, and so the set that is defined will be a finite union of intervals having the parameters $y_{i}$ as endpoints, with the intervals being open or closed depending on whether the parameters themselves satisfy the formula or not.

Theory of successor

Let us next consider the theory of a successor function, as realized for example in the Dedekind model, $⟨ N, S, 0 ⟩$ , where $S$ is the successor
function $S n = n + 1$ . The theory has the following three axioms:
$\forall x (S x \neq 0)$

$\forall x, y (S x = S y ⟹ x = y)$

$\forall x (x \neq 0 ⟹ \exists y (S y = x)) .$
In the Dedekind model, every individual is definable, since $x = n$ just in case $x = S S \dots S 0$ , where we have $n$ iterative applications of $S$ . So this is a pointwise definable model, and hence also Leibnizian. Note the interplay between the $n$ of the object theory and $n$ of the metatheory in the claim that every individual is definable.

What definable subsets of the Dedekind model can we think of? Of course, we can define any particular finite set, since the numbers are definable as individuals. For example, we can define the set $1, 5, 8$ by saying, “either $x$ has the defining property of $1$ or it has the defining property of $5$ or it has the defining property of $8$ .” Thus any finite set is definable, and by negating such a formula, we see also that any cofinite set—the complement of a finite set—is definable. Are there any other definable sets? For example, can we define the set of even numbers? How could we prove that we cannot? The Dedekind structure has no automorphisms, since all the individuals are definable, and so we cannot expect to use automorphism to show that the even numbers are not definable as a set. We need a deeper understanding of definability and truth in this structure.

Theorem. The theory of a successor function admits elimination of quantifiers—every assertion is equivalent in this theory to a quantifier-free assertion.

Proof. By induction on formulas. The claim is already true for atomic assertions, since they have no quantifiers, and quantifier-free assertions are clearly closed under the Boolean connectives. So it suffices by induction to eliminate the quantifier from assertions of the form $\exists x φ (x, \dots)$ , where $φ$ is quantifier free. We may place $φ$ in disjunctive normal form, and since the quantifier distributes over disjunction, we reduce to the case that $φ$ is a conjunction of atomic and negated atomic assertions. We may assume that $x$ appears in each atomic conjunct, since otherwise we may bring that conjunct outside the quantifier. We may furthermore assume that $x$ appears on only one side of each atomic clause, since otherwise the statement is either trivially true as with $S S x = S S x$ or $S x \neq S S x$ , or trivially false as with $S x = S S x$ . Consider for example:
$\exists x [(S S S x = y) \land (S S y = S S S z) \land (S S S S S x = S S S w) \land$
$\land (S x \neq S S S S w) \land (S S S S y \neq S S S S S z)]$
We can remove duplicated $S$ s occurring on both sides of an equation. If $x = S^{k} y$ appears, we can get rid of $x$ and replace all occurrences with $S^{k} y$ . If $S^{n} x = y$ appears, can add $S$ ’s everywhere and then replace any occurrence of $S^{n} x$ with $y$ . If only inequalities appear, then the statement is simply true.

For example, since the third clause in the formula above is equivalent to $S S x = w$ , we may use that to omit any need to refer to $x$ , and the formula overall is equivalent to
$(S w = y) \land (y = S z) \land (w \neq S S S S S w) \land (y \neq S z),$ which has no quantifiers.
Since the method is completely general, we have proved that the theory of successor admits elimination of quantifiers.

It follows that the definable sets in the Dedekind model $⟨ N, S, 0 ⟩$ , using only the first-order language of this structure, are precisely the finite and cofinite sets.

Corollary. The definable sets in $⟨ N, S, 0 ⟩$ are precisely the finite and cofinite sets

Proof. This is because an atomic formula defines a finite set, and the collection of finite or cofinite sets is closed under negation and Boolean combinations. Since every formula is equivalent to a quantifier-free formula, it follows that every formula is a Boolean combination of atomic formulas, and hence defines a finite or cofinite set.

In particular, the concepts of being even or being odd are not definable from the successor operation in $⟨ N, S, 0 ⟩$ , since the set of even numbers is neither finite nor cofinite.

Corollary. The theory of a successor function is complete—it is the theory of the standard model $⟨ N, S, 0 ⟩$ .

Proof. If $σ$ is a sentence in the language of successor, then by the quantifier-elimination theorem it is equivalent to a quantifier-free assertion in the language with the successor function $S$ and constant symbol $0$ . But the only quantifier-free sentences in this language are Boolean combinations of equations of the form $S^{n} 0 = S^{k} 0$ . Since all such equations are settled by the theory, the sentence itself is settled by the theory, and so the theory is complete.

We saw that the three axioms displayed on the previous page were true in the Dedekind model $⟨ N, S, 0 ⟩$ . Are there any other models of these axioms? Yes, there are. For example, we can add another $Z$ -chain of successors on the side, as with $N + Z$ or $N ⊔ Z$ , although we shall see that the order is not definable. What are the definable elements in the enlarged structure? Still $0$ and all its finite successors are definable as before. But no elements of the $Z$ -chains can be definable, because we may perform an automorphism of the structure that translates elements within the $Z$ -chain by a fixed amount.

Let me prove next that the theory implies the induction axiom schema.

Corollary. The theory of successor (the three axioms) implies the induction axiom schema in the language of successor, that is, the following assertion for any assertion $φ (x)$ :
$[φ (0) \land (\forall x (φ (x) ⟹ φ (S x))] ⟹ \forall x φ (x)$

Proof. Consider the set defined by $φ (x)$ . By the earlier corollary, it must be eventually periodic in the standard model $⟨ N, S, 0 ⟩$ . But by the induction assumption stated in the theorem, it must hold of every number in the standard model. So the standard model thinks that $\forall x φ (x)$ . But the theory of the standard model is the theory of successor, which is complete. So the theory of successor entails that $φ$ is universal, as desired.

In other words, in the trivial theory of successor–the three axioms—we get the corresponding induction axiom for free.

Presburger arithmetic

Presburger arithmetic is the theory of addition on the natural numbers, that is, the theory of the structure $⟨ N, +, 0, 1 ⟩$ . The numbers $0$ and $1$ are actually definable here from addition alone, since $0$ is the unique additive identity, and $1$ is the only number $u$ that is not expressible as a sum $x + y$ with both $x \neq u$ and $y \neq u$ . So we may view this model if desired as a definitional expansion of $⟨ N, + ⟩$ , with addition only. The number $2$ is similarly definable as $1 + 1$ , and indeed any number $n$ is definable as $1 + \dots + 1$ , with $n$ summands, and so this is a pointwise definable model and hence also Leibnizian.

What are the definable subsets? We can define the even numbers, of course, since $x$ is even if and only if $\exists y (y + y = x)$ . We can similarly define congruence modulo $2$ by $x \equiv_{2} y ⟺ \exists z [(z + z + x = y) \lor (z + z + y = x)]$ . More generally, we can express the relation of congruence modulo $n$ for any fixed $n$ as follows:
$x \equiv_{n} y if and only if \exists z [(\overset{n}{\overset{⏞}{z + \dots + z}} + x = y) \lor (\overset{n}{\overset{⏞}{z + \dots + z}} + y = x)] .$
What I claim is that this exhausts what is expressible.

Theorem. Presburger arithmetic in the definitional expansion with all congruence relations, that is, the theory of the structure
$⟨ N, +, 0, 1, \equiv_{2}, \equiv_{3}, \equiv_{4}, \dots ⟩$
admits elimination of quantifiers. In particular, every assertion in the language of $⟨ N, +, 0, 1 ⟩$ is equivalent to a quantifer-free assertion in the language with the congruence relations.

Proof. We consider Presburger arithmetic in the language with addition $+$ , with all the congruence relations $\equiv_{n}$ for every $n \geq 2$ , and the constants $0$ and $1$ . We prove quantifier-elimination in this language by induction on formulas. As before the claim already holds for atomic assertions and is preserved by Boolean connectives. So it suffices to eliminate the quantifier from assertions of the form $\exists x φ (x, \dots)$ , where $φ$ is quantifier-free. By placing $φ$ into disjunctive normal form and distributing the quantifier over the disjunction, we may assume that $φ$ is a conjunction of atomic and negated atomic assertions. Note that negated congruences are equivalent to a disjunction of positive congruences, such as in the case:
$x ≢_{4} y if and only if (x + 1 \equiv_{4} y) \lor (x + 1 + 1 \equiv_{4} y) \lor (x + 1 + 1 + 1 \equiv_{4} y) .$
We may therefore assume there are no negated congruences in $φ$ . By canceling like terms on each side of an equation or congruence, we may assume that $x$ occurs on only one side. We may assume that $x$ occurs nontrivially in every conjunct of $φ$ , since otherwise this conjunct commutes outside the quantifier. Since subtraction modulo $n$ is the same as adding $n - 1$ times, we may also assume that all congruences occurring in $φ$ have the form $k x \equiv_{n} t$ , where $k x$ denotes the syntactic expression $x + \dots + x$ occurring in the formula, with $k$ summands, and $t$ is a term not involving the variable $x$ . Thus, $φ$ is a conjunction of expressions each having the form $k x \equiv_{n} t$ , $a x + r = s$ , or $b x + u \neq v$ , where $a x$ and $b x$ similarly denote the iterated sums $x + \dots + x$ and $r, s, u, v$ are terms not involving $x$ .

If indeed there is a conjunct of the equality form $a x + r = s$ occurring in $φ$ , then we may omit the quantifier as follows. Namely, in order to fulfill the existence assertion, we know that $x$ will have to solve $a x + r = s$ , and so in particular $r \equiv_{a} s$ , which ensures the existence of such an $x$ , but also in this case any inequality $b x + u \neq v$ can be equivalently expressed as $a b x + a u \neq a v$ , which since $a x + r = s$ is equivalent to $b s + a u \neq a v + b r$ , and this does does not involve $x$ ; similarly, any congruence $k x \equiv_{n} t$ is equivalent to $a k x \equiv_{a n} a t$ , which is equivalent to $s \equiv_{a n} r + a t$ , which again does not involve $x$ . Thus, when there is an equality involving $x$ present in $φ$ , then we can use that fact to express the whole formula in an equivalent manner not involving $x$ .

So we have reduced to the case $\exists x φ$ , where $φ$ is a conjunction of inequalities $b s + u \neq v$ and congruences $k x \equiv_{n} t$ . We can now ignore the inequalities, since if the congruence system has a solution, then it will have infinitely many solutions, and so there will be an $x$ solving any finitely given inequalities. So we may assume that $φ$ is simply a list of congruences of the form $k x \equiv_{n} t$ , and the assertion is that this system of congruences has a solution. But there are only finitely many congruences mentioned, and so by working modulo the least common multiple of the bases that occur, there are only finitely many possible values for $x$ to be checked. And so we can simply replace $φ$ with a disjunction over these finitely many values $i$ , replacing $x$ in each conjunction with $1 + \dots + 1$ , using $i$ copies of $1$ , for each $i$ up to the least common multiples of the bases that arise in the congruences appearing in $φ$ . If there is an $x$ solving the system, then one of these values of $i$ will work, and conversely.

So we have ultimately succeeded in expressing $\exists x φ$ in a quantifier-free manner, and so by induction every assertion in Presburger arithmetic is equivalent to a quantifier-free assertion in the language allowing addition, congruences, and the constants $0$ and $1$ .

Corollary. The definable sets in $⟨ N, +, 0, 1 ⟩$ are exactly the eventually periodic sets.

Proof. Every periodic set is definable, since one can specify the set up to the period $p$ , and then express the invariance modulo $p$ . Any finite deviation from a definable set also is definable, since every individual number is definable. So every eventually period set is definable. Conversely, every definable set is defined by a quantifier-free assertion in the language of $⟨ N, +, 0, 1, \equiv_{2}, \equiv_{3}, \equiv_{4}, \dots ⟩$ . We may place the definition in disjunctive normal form, and again replace negated congruences with a disjunction of positive congruences. For large enough values of $x$ , the equalities and inequalities appearing in the definition become irrelevant, and so the definition eventually agrees with a finite union of solutions of congruence systems. Every such system is periodic with a period at most the least common multiple of the bases of the congruences appearing in it. And so every definable set is eventually periodic, as desired.

Corollary. Multiplication is not definable in $⟨ N, +, 0, 1 ⟩$ . Indeed, the squaring operation is not definable, and neither is the divisibility relation $p ∣ q$ .

Proof. If we could define multiplication, or even the squaring operation, then we would be able to define the set of perfect squares, but this is not eventually periodic. Similarly, if we could define the divides relation $p ∣ q$ , then we could define the set of prime numbers, which is not eventually periodic.

Real-closed field

Let us lastly consider the ordered real field $⟨ R, +, \cdot, 0, 1, < ⟩$ . I want to mention (without proof) that a deep theorem of Tarski shows that this structure admits elimination of quantifiers: every assertion is equivalent in this structure to a quantifier-free assertion. In fact all that is need is that this is a real-closed field, an ordered field in which every odd-degree polynomial has a root and every positive number has a square root.

We can begin to gain insight to this fact by reaching into the depths of our high-school education. Presented with an equation $a x^{2} + b x + c = 0$ in the integers, we know by the quadratic formula that the solution is $x = (- b \pm \sqrt{b^{2} - 4 a c}) / 2 a$ , and in particular, there is a solution in the real numbers if and only if $b^{2} - 4 a c \geq 0$ , since otherwise a negative discriminant means the solution is a complex number. In other words,
$\exists x (a x^{2} + b x + c = 0) if and only if b^{2} - 4 a c \geq 0.$
The key point is that this an elimination of quantifiers result, since we have eliminated the quantifier $\exists x$ .

Tarski’s theorem proves more generally that every assertion in the language of ordered fields is equivalent in real-closed fields to a quantifier-free assertion. Furthermore, there is a computable procedure to find the quantifier-free equivalent, as well as a computable procedure to determine the truth of any quantifier-free assertion in the theory of real-closed fields.

What I find incredible is that it follows from this that there is a computable procedure to determine the truth of any first-order assertion of Cartesian plane geometry, since all such assertions are expressible in the language of $⟨ R, +, \cdot, 0, 1, < ⟩$ . Amazing! I view this as an incredible culmination of two thousand years of mathematical investigation: we now have an algorithm to determine by rote procedure the truth of any statement in Cartesian geometry. Meanwhile, a counterpoint is that the decision procedure, unfortunately, is not computationally feasible, however, since it takes more than exponential time, and it is a topic of research to investigate the computational running time of the best algorithms.

An algebra of orders

Posted on August 20, 2021 by Joel David Hamkins

Did you know that you can add and multiply orders? For any two order structures $A$ and $B$ , we can form the ordered sum $A + B$ and ordered product $A \otimes B$ , and other natural operations, such as the disjoint sum $A ⊔ B$ , which make altogether an arithmetic of orders. We combine orders with these operations to make new orders, often with interesting properties. Let us explore the resulting algebra of orders!

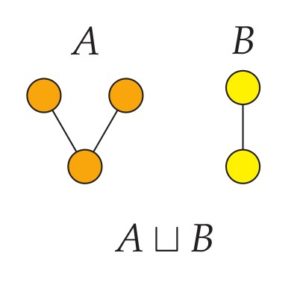
One of the most basic operations that we can use to combine two orders is the disjoint sum operation $A ⊔ B$ . This is the order resulting from placing a copy of $A$ adjacent to a copy of $B$ , side-by-side, forming a combined order with no instances of the order relation between the two parts. If $A$ is the orange $\lor$ -shaped order here and $B$ is the yellow linear order, for example, then $A ⊔ B$ is the combined order with all five nodes.

Another kind of addition is the ordered sum of two orders $A + B$ , which is obtained by placing a copy of $B$ above a copy of $A$ , as indicated here by adding the orange copy of $A$ and the yellow copy of $B$ . Also shown is the sum $B + A$ , with the summands reversed, so that we take $B$ below and $A$ on top. It is easy to check that the ordered sum of two orders is an order. One notices immediately, of course, that the resulting ordered sums $A + B$ and $B + A$ are not the same! The order $A + B$ has a greatest element, whereas $B + A$ has two maximal elements. So the ordered sum operation on orders is not commutative. Nevertheless, we shall still call it addition. The operation, which has many useful and interesting features, goes back at least to the 19th century with Cantor, who defined the addition of well orders this way.

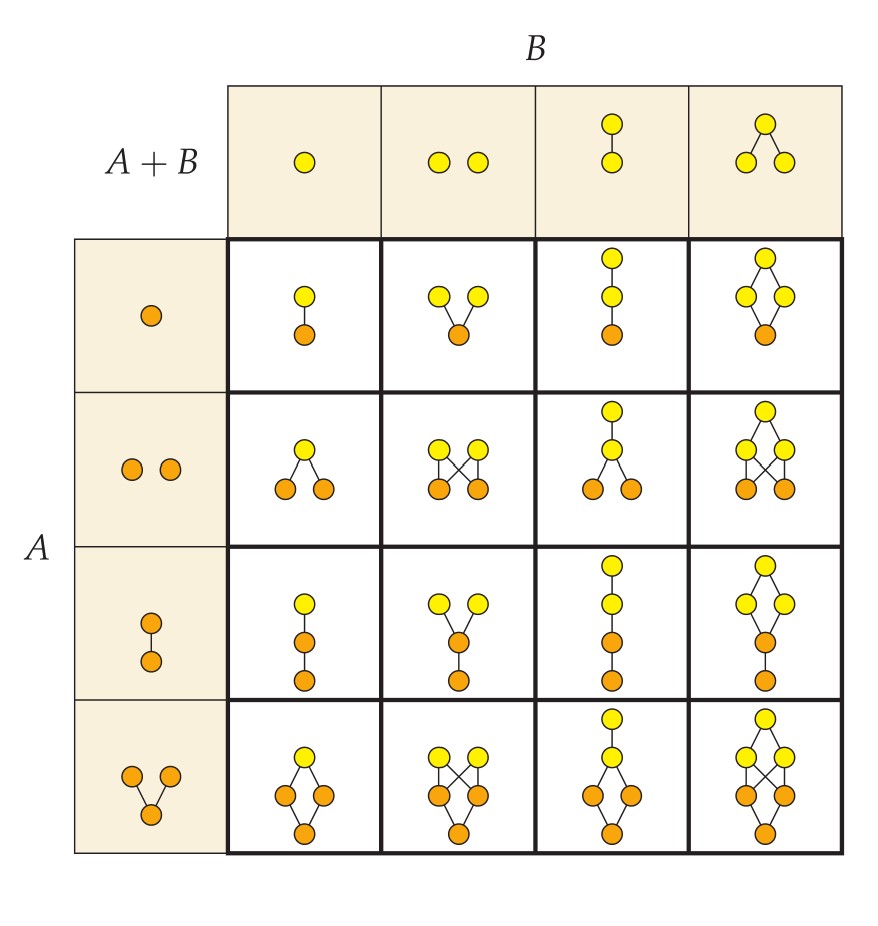
In order to illustrate further examples, I have assembled here an addition table for several simple finite orders. The choices for $A$ appear down the left side and those for $B$ at the top, with the corresponding sum $A + B$ displayed in each cell accordingly.

We can combine the two order addition operations, forming a variety of other orders this way.

The reader is encouraged to explore further how to add various finite orders using these two forms of addition. What is the smallest order that you cannot generate from $1$ using $+$ and $⊔$ ? Please answer in the comments.

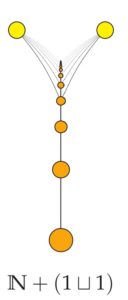We can also add infinite orders. Displayed here, for example, is the order $N + (1 ⊔ 1)$ , the natural numbers wearing two yellow caps. The two yellow nodes at the top form a copy of $1 ⊔ 1$ , while the natural numbers are the orange nodes below. Every natural number (yes, all infinitely many of them) is below each of the two nodes at the top, which are incomparable to each other. Notice that even though we have Hasse diagrams for each summand order here, there can be no minimal Hasse diagram for the sum, because any particular line from a natural number to the top would be implied via transitivity from higher such lines, and we would need such lines, since they are not implied by the lower lines. So there is no minimal Hasse diagram.

This order happens to illustrate what is called an exact pair, which occurs in an order when a pair of incomparable nodes bounds a chain below, with the property that any node below both members of the pair is below something in the chain. This phenomenon occurs in sometimes unexpected contexts—any countable chain in the hierarchy of Turing degrees in computability theory, for example, admits an exact pair.

Let us turn now to multiplication. The ordered product $A \otimes B$ is the order resulting from having $B$ many copies of $A$ . That is, we replace each node of $B$ with an entire copy of the $A$ order. Within each of these copies of $A$ , the order relation is just as in $A$ , but the order relation between nodes in different copies of $A$ , we follow the $B$ relation. It is not difficult to check that indeed this is an order relation. We can illustrate here with the same two orders we had earlier.

In forming the ordered product $A \otimes B$ , in the center here, we take the two yellow nodes of $B$ , shown greatly enlarged in the background, and replace them with copies of $A$ . So we have ultimately two copies of $A$ , one atop the other, just as $B$ has two nodes, one atop the other. We have added the order relations between the lower copy of $A$ and the upper copy, because in $B$ the lower node is related to the upper node. The order $A \otimes B$ consists only of the six orange nodes—the large highlighted yellow nodes of $B$ here serve merely as a helpful indication of how the product is formed and are not in any way part of the product order $A \otimes B$ .

Similarly, with $B \otimes A$ , at the right, we have the three enlarged orange nodes of $B$ in the background, which have each been replaced with copies of $A$ . The nodes of each of the lower copies of $A$ are related to the nodes in the top copy, because in $B$ the two lower nodes are related to the upper node.

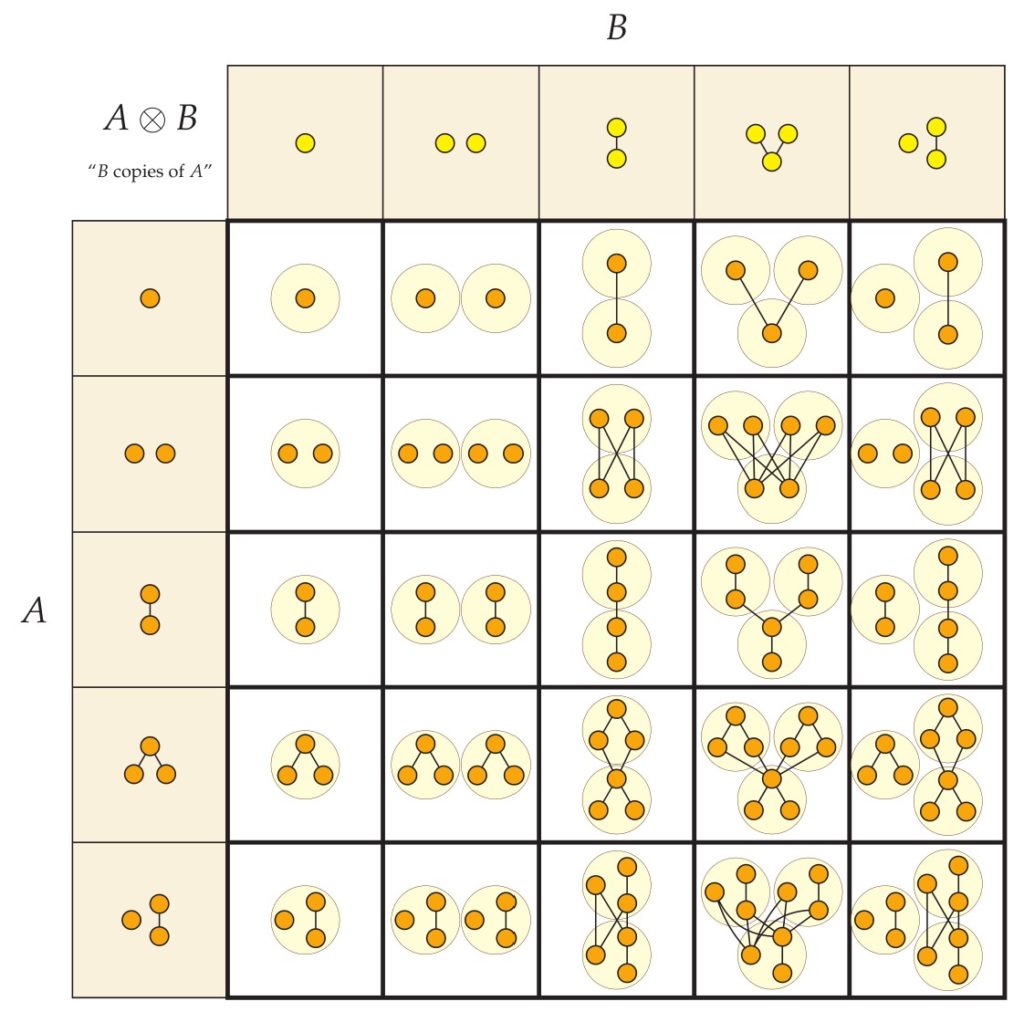
I have assembled a small multiplication table here for some simple finite orders.

So far we have given an informal account of how to add and multiply ordered ordered structures. So let us briefly be a little more precise and formal with these matters.

In fact, when it comes to addition, there is a slightly irritating matter in defining what the sums $A ⊔ B$ and $A + B$ are exactly. Specifically, what are the domains? We would like to conceive of the domains of $A ⊔ B$ and $A + B$ simply as the union the domains of $A$ and $B$ —we’d like just to throw the two domains together and form the sums order using that combined domain, placing $A$ on the $A$ part and $B$ on the $B$ part (and adding relations from the $A$ to the $B$ part for $A + B$ ). Indeed, this works fine when the domains of $A$ and $B$ are disjoint, that is, if they have no points in common. But what if the domains of $A$ and $B$ overlap? In this case, we can’t seem to use the union in this straightforward manner. In general, we must disjointify the domains—we take copies of $A$ and $B$ , if necessary, on domains that are disjoint, so that we can form the sums $A ⊔ B$ and $A + B$ on the union of those nonoverlapping domains.

What do we mean precisely by “taking a copy” of an ordered structure $A$ ? This way of talking in mathematics partakes in the philosophy of structuralism. We only care about our mathematical structures up to isomorphism, after all, and so it doesn’t matter which isomorphic copies of $A$ and $B$ we use; the resulting order structures $A ⊔ B$ will be isomorphic, and similarly for $A + B$ . In this sense, we are defining the sum orders only up to isomorphism.

Nevertheless, we can be definite about it, if only to verify that indeed there are copies of $A$ and $B$ available with disjoint domains. So let us construct a set-theoretically specific copy of $A$ , replacing each individual $a$ in the domain of $A$ with $(a, orange)$ , for example, and replacing the elements $b$ in the domain of $B$ with $(b, yellow)$ . If “orange” is a specific object distinct from “yellow,” then these new domains will have no points in common, and we can form the disjoint sum $A ⊔ B$ by using the union of these new domains, placing the $A$ order on the orange objects and the $B$ order on the yellow objects.

Although one can use this specific disjointifying construction to define what $A ⊔ B$ and $A + B$ mean as specific structures, I would find it to be a misunderstanding of the construction to take it as a suggestion that set theory is anti-structuralist. Set theorists are generally as structuralist as they come in mathematics, and in light of Dedekind’s categorical account of the natural numbers, one might even find the origin of the philosophy of structuralism in set theory. Rather, the disjointifying construction is part of the general proof that set theory abounds with isomorphic copies of whatever mathematical structure we might have, and this is part of the reason why it serves well as a foundation of mathematics for the structuralist. To be a structuralist means not to care which particular copy one has, to treat one’s mathematical structures as invariant under isomorphism.

But let me mention a certain regrettable consequence of defining the operations by means of a specific such disjointifying construction in the algebra of orders. Namely, it will turn out that neither the disjoint sum operation nor the ordered sum operation, as operations on order structures, are associative. For example, if we use $1$ to represent the one-point order, then $1 ⊔ 1$ means the two-point side-by-side order, one orange and one yellow, but really what we mean is that the points of the domain are ${(a, orange), (a, yellow)}$ , where the original order is on domain ${a}$ . The order $(1 ⊔ 1) ⊔ 1$ then means that we take an orange copy of that order plus a single yellow point. This will have domain
${((a, orange), orange), ((a, yellow), orange), (a, yellow)}$
The order $1 ⊔ (1 ⊔ 1)$ , in contrast, means that we take a single orange point plus a yellow copy of $1 ⊔ 1$ , leading to the domain
${(a, orange), ((a, orange), yellow), ((a, yellow), yellow)}$
These domains are not the same! So as order structures, the order $(1 ⊔ 1) ⊔ 1$ is not identical with $1 ⊔ (1 ⊔ 1)$ , and therefore the disjoint sum operation is not associative. A similar problem arises with $1 + (1 + 1)$ and $(1 + 1) + 1$ .

But not to worry—we are structuralists and care about our orders here only up to isomorphism. Indeed, the two resulting orders are isomorphic as orders, and more generally, $(A ⊔ B) ⊔ C$ is isomorphic to $A ⊔ (B ⊔ C)$ for any orders $A$ , $B$ , and $C$ , and similarly with $A + (B + C) ≅ (A + B) + C$ , as discussed with the theorem below. Furthermore, the order isomorphism relation is a congruence with respect to the arithmetic we have defined, which means that $A ⊔ B$ is isomorphic to $A^{'} ⊔ B^{'}$ whenever $A$ and $B$ are respectively isomorphic to $A^{'}$ and $B^{'}$ , and similarly with $A + B$ and $A \otimes B$ . Consequently, we can view these operations as associative, if we simply view them not as operations on the order structures themselves, but on their order-types, that is, on their isomorphism classes. This simple abstract switch in perspective restores the desired associativity. In light of this, we are free to omit the parentheses and write $A ⊔ B ⊔ C$ and $A + B + C$ , if care about our orders only up to isomorphism. Let us therefore adopt this structuralist perspective for the rest of our treatment of the algebra of orders.

Let us give a more precise formal definition of $A \otimes B$ , which requires no disjointification. Specifically, the domain is the set of pairs ${(a, b) ∣ a \in A, b \in B}$ , and the order is defined by $(a, b) \leq_{A \otimes B} (a^{'}, b^{'})$ if and only if $b \leq_{B} b^{'}$ , or $b = b^{'}$ and $a \leq_{A} a^{'}$ . This order is known as the reverse lexical order, since we are ordering the nodes in the dictionary manner, except starting from the right letter first rather than the left as in an ordinary dictionary. One could of course have defined the product using the lexical order instead of the reverse lexical order, and this would give $A \otimes B$ the meaning of “ $A$ copies of $B$ .” This would be a fine alternative and in my experience mathematicians who rediscover the ordered product on their own often tend to use the lexical order, which is natural in some respects. Nevertheless, there is a huge literature with more than a century of established usage with the reverse lexical order, from the time of Cantor, who defined ordinal multiplication $α β$ as $β$ copies of $α$ . For this reason, it seems best to stick with the reverse lexical order and the accompanying idea that $A \otimes B$ means “ $B$ copies of $A$ .” Note also that with the reverse lexical order, we shall be able to prove left distributivity $A \otimes (B + C) = A \otimes B + A \otimes C$ , whereas with the lexical order, one will instead have right distributivity $(B + C) \otimes^{*} A = B \otimes^{*} A + C \otimes^{*} A$ .

Let us begin to prove some basic facts about the algebra of orders.

Theorem. The following identities hold for orders $A$ , $B$ , and $C$ .

Associativity of disjoint sum, ordered sum, and ordered product. $\begin{array}{rcl} A ⊔ (B ⊔ C) & ≅ & (A ⊔ B) ⊔ C \\ A + (B + C) & ≅ & (A + B) + C \\ A \otimes (B \otimes C) & ≅ & (A \otimes B) \otimes C \end{array}$
Left distributivity of product over disjoint sum and ordered sum. $\begin{array}{rcl} A \otimes (B ⊔ C) & ≅ & (A \otimes B) ⊔ (A \otimes C) \\ A \otimes (B + C) & ≅ & (A \otimes B) + (A \otimes C) \end{array}$

In each case, these identities are clear from the informal intended meaning of the orders. For example, $A + (B + C)$ is the order resulting from having a copy of $A$ , and above it a copy of $B + C$ , which is a copy of $B$ and a copy of $C$ above it. So one has altogether a copy of $A$ , with a copy of $B$ above that and a copy of $C$ on top. And this is the same as $(A + B) + C$ , so they are isomorphic.

One can also aspire to give a detailed formal proof verifying that our color-coded disjointifying process works as desired, and the reader is encouraged to do so as an exercise. To my way of thinking, however, such a proof offers little in the way of mathematical insight into algebra of orders. Rather, it is about checking the fine print of our disjointifying process and making sure that things work as we expect. Several of the arguments can be described as parenthesis-rearranging arguments—one extracts the desired information from the structure of the domain order and puts that exact same information into the correct form for the target order.

For example, if we have used the color-scheme disjointifying process described above, then the elements of $A ⊔ (B ⊔ C)$ each have one of the following forms, where $a \in A$ , $b \in B$ , and $c \in C$ :
$(a, orange)$
$((b, orange), yellow)$
$((c, yellow), yellow)$
We can define the color-and-parenthesis-rearranging function $π$ to put them into the right form for $(A ⊔ B) ⊔ C$ as follows:
$\begin{aligned} π : (a, orange) & \mapsto ((a, orange), orange) \\ π : ((b, orange), yellow) & \mapsto ((b, yellow), orange) \\ π : ((c, yellow), yellow) & \mapsto (c, yellow) \end{aligned}$
In each case, we will preserve the order, and since the orders are side-by-side, the cases never interact in the order, and so this is an isomorphism.

Similarly, for distributivity, the elements of $A \otimes (B ⊔ C)$ have the two forms:
$(a, (b, orange))$
$(a, (c, yellow))$
where $a \in A$ , $b \in B$ , and $c \in C$ . Again we can define the desired ismorphism $τ$ by putting these into the right form for $(A \otimes B) ⊔ (A \otimes C)$ as follows:
$\begin{aligned} τ : (a, (b, orange)) & \mapsto ((a, b), orange) \\ τ : (a, (c, yellow)) & \mapsto ((a, c), yellow) \end{aligned}$
And again, this is an isomorphism, as desired.

Since order multiplication is not commutative, it is natural to inquire about the right-sided distributivity laws:
$\begin{array}{rcl} (B + C) \otimes A & \overset{?}{≅} & (B \otimes A) + (C \otimes A) \\ (B ⊔ C) \otimes A & \overset{?}{≅} & (B \otimes A) ⊔ (C \otimes A) \end{array}$
Unfortunately, however, these do not hold in general, and the following instances are counterexamples. Can you see what to take as $A$ , $B$ , and $C$ ? Please answer in the comments.

Theorem.

If $A$ and $B$ are linear orders, then so are $A + B$ and $A \otimes B$ .
If $A$ and $B$ are nontrivial linear orders and both are endless, then $A + B$ is endless; if at least one of them is endless, then $A \otimes B$ is endless.
If $A$ is an endless dense linear order and $B$ is linear, then $A \otimes B$ is an endless dense linear order.
If $A$ is an endless discrete linear order and $B$ is linear, then $A \otimes B$ is an endless discrete linear order.

Proof. If both $A$ and $B$ are linear orders, then it is clear that $A + B$ is linear. Any two points within the $A$ copy are comparable, and any two points within the $B$ copy, and every point in the $A$ copy is below any point in the $B$ copy. So any two points are comparable and thus we have a linear order. With the product $A \otimes B$ , we have $B$ many copies of $A$ , and this is linear since any two points within one copy of $A$ are comparable, and otherwise they come from different copies, which are then comparable since $B$ is linear. So $A \otimes B$ is linear.

For statement (2), we know that $A + B$ and $A \otimes B$ are nontrivial linear orders. If both $A$ and $B$ are endless, then clearly $A + B$ is endless, since every node in $A$ has something below it and every node in $B$ has something above it. For the product $A \otimes B$ , if $A$ is endless, then every node in any copy of $A$ has nodes above and below it, and so this will be true in $A \otimes B$ ; and if $B$ is endless, then there will always be higher and lower copies of $A$ to consider, so again $A \otimes B$ is endless, as desired.

For statement (3), assume that $A$ is an endless dense linear and that $B$ is linear. We know from (1) that $A \otimes B$ is a linear order. Suppose that $x < y$ in this order. If $x$ and $y$ live in the same copy of $A$ , then there is a node $z$ between them, because $A$ is dense. If $x$ occurs in one copy of $A$ and $B$ in another, then because $A$ is endless, there will a node $z$ above $x$ in its same copy, leading to $x < z < y$ as desired. (Note: we don’t need $B$ to be dense.)

For statement (4), assume instead that $A$ is an endless discrete linear order and $B$ is linear. We know that $A \otimes B$ is a linear order. Every node of $A \otimes B$ lives in a copy of $A$ , where it has an immediate successor and an immediate predecessor, and these are also immediate successor and predecessor in $A \otimes B$ . From this, it follows also that $A \otimes B$ is endless, and so it is an endless discrete linear order.

The reader is encouraged to consider as an exercise whether one can drop the “endless” hypotheses in the theorem. Please answer in the comments.

Theorem. The endless discrete linear orders are exactly those of the form $Z \otimes L$ for some linear order $L$ .

Proof. If $L$ is a linear order, then $Z \otimes L$ is an endless discrete linear order by the theorem above, statement (4). So any order of this form has the desired feature. Conversely, suppose that $P$ is an endless discrete linear order. Define an equivalence relation for points in this order by which $p \sim q$ if and only $p$ and $q$ are at finite distance, in the sense that there are only finitely many points between them. This relation is easily seen to be reflexive, transitive and symmetric, and so it is an equivalence relation. Since $P$ is an endless discrete linear order, every object in the order has an immediate successor and immediate predecessor, which remain $\sim$ -equivalent, and from this it follows that the equivalence classes are each ordered like the integers $Z$ , as indicated by the figure here.

The equivalence classes amount to a partition of $P$ into disjoint segments of order type $Z$ , as in the various colored sections of the figure. Let $L$ be the induced order on the equivalence classes. That is, the domain of $L$ consists of the equivalence classes $P / \sim$ , which are each a $Z$ chain in the original order, and we say $[a] <_{L} [b]$ just in case $a <_{P} b$ . This is a linear order on the equivalence classes. And since $P$ is $L$ copies of its equivalence classes, each of which is ordered like $Z$ , it follows that $P$ is isomorphic to $Z \otimes L$ , as desired.

(Interested readers are advised that the argument above uses the axiom of choice, since in order to assemble the isomorphism of $P$ with $Z \otimes L$ , we need in effect to choose a center point for each equivalence class.)

If we consider the integers inside the rational order $Z \subseteq Q$ , it is clear that we can have a discrete suborder of a dense linear order. How about a dense suborder of a discrete linear order?

Question. Is there a discrete linear order with a suborder that is a dense linear order?

What? How could that happen? In my experience, mathematicians first coming to this topic often respond instinctively that this should be impossible. I have seen sophisticated mathematicians make such a pronouncement when I asked the audience about it in a public lecture. The fundamental nature of a discrete order, after all, is completely at odds with density, since in a discrete order, there is a next point up and down, and a next next point, and so on, and this is incompatible with density.

Yet, surprisingly, the answer is Yes! It is possible—there is a discrete order with a suborder that is densely ordered. Consider the extremely interesting order $Z \otimes Q$ , which consists of $Q$ many copies of $Z$ , laid out here increasing from left to right. Each tiny blue dot is a rational number, which has been replaced with an entire copy of the integers, as you can see in the magnified images at $a$ , $b$ , and $c$ .

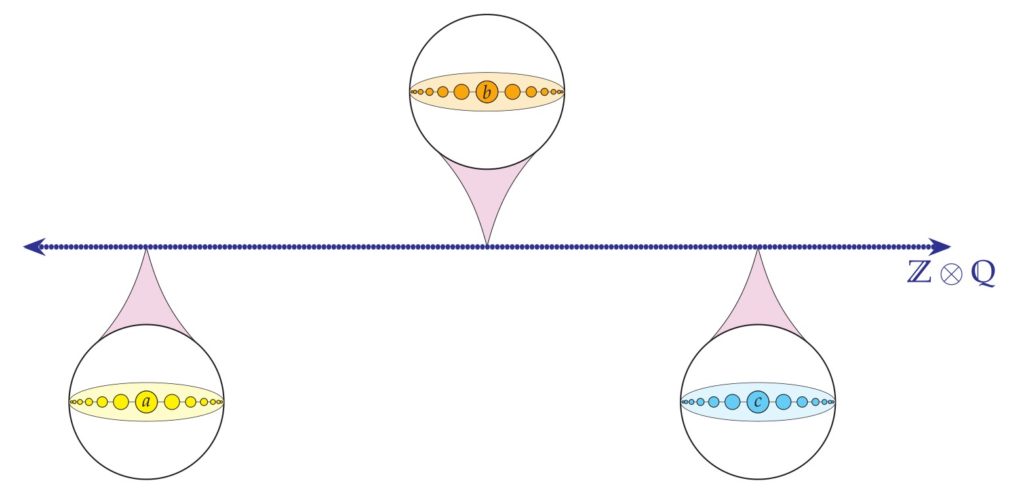
The order is quite subtle, and so let me also provide an alternative presentation of it. We have many copies of $Z$ , and those copies are densely ordered like $Q$ , so that between any two copies of $Z$ is another one, like this:

Perhaps it helps to imagine that the copies of $Z$ are getting smaller and smaller as you squeeze them in between the larger copies. But you can indeed always fit another copy of $Z$ between, while leaving room for the further even tinier copies of $Z$ to come.

The order $Z \otimes Q$ is discrete, in light of the theorem characterizing discrete linear orders. But also, this is clear, since every point of $Z \otimes Q$ lives in its local copy of $Z$ , and so has an immediate successor and predecessor there. Meanwhile, if we select exactly one point from each copy of $Z$ , the $0$ of each copy, say, then these points are ordered like $Q$ , which is dense. Thus, we have proved:

Theorem. The order $Z \otimes Q$ is a discrete linear order having a dense linear order as a suborder.

One might be curious now about the order $Q \otimes Z$ , which is $Z$ many copies of $Q$ . This order, however, is a countable endless dense linear order, and therefore is isomorphic to $Q$ itself.

This material is adapted from my book-in-progress, Topics in Logic, drawn from Chapter 3 on Relational Logic, which incudes an extensive section on order theory, of which this is an important summative part.

Linear gradings of partial orders

Posted on August 14, 2021 by Joel David Hamkins

Order relations are often fruitfully conceived as being stratified into “levels” in a natural way. The level structure is meant to be compatible with the order, in the sense that as one moves strictly up in the order, one also ascends successively from lower levels to strictly higher levels. With the simple order relation pictured here, for example, we might naturally imagine the least element $0$ on a bottom level, the three middle nodes $a$ , $b$ , and $c$ on an intermediate level, and node $1$ on a level at the top. With this level structure, as we move up strictly in the order, then we also move up strictly in the hierarchy of levels.

What exactly is a level? Let us be a little more precise. We can depict the intended level structure of our example order more definitely as in the figure here. At the left appears the original order relation, while the yellow highlighted bands organize the nodes into three levels, with node $0$ on the bottom level, nodes $a$ , $b$ , and $c$ on the middle level, and node $1$ on the top level. This level structure in effect describes a linear preorder relation $\leq$ for which $0 \leq a, b, c \leq 1$ , with the three intermediate nodes all equivalent with respect to this preorder—they are on the same level.

Thus, we realize that a level structure of an order relation is simply a linear preorder relation that respects strict instances of the original order, and the levels are simply the equivalence classes of the preorder. More precisely, we define that a linear grading of an order relation $⟨ A, ≼ ⟩$ is a linear preorder relation $\leq$ on $A$ for which every strict instance of the original order is also graded strictly by the linear preorder; that is, we require that
$a ≺ b implies a < b$ Thus, any strictly lower point in the original order is on a lower level, and we define that objects are on the same level if they are equivalent with respect to the preorder. A linearly graded order is a relational structure $⟨ A, ≼, \leq ⟩$ with two orders on the same domain, the first $≼$ being an order relation on $A$ and the second $\leq$ being a linear preorder relation that grades the first order.

It turns out that there are often far more ways to stratify a given order by levels than one might have expected. For the simple order above, for example, there are thirteen distinct linear grading orders, as shown here.

The conclusion is inescapable that the level concept is not inherent in the order relation itself, for a given order relation may admit a huge variety of different level hierarchies, each of them compatible with the given order.

One should therefore not make the mistake of thinking that if one has an order relation, such as a philosophical reduction notion of some kind or a supervenience relation, then one is automatically entitled to speak of “levels” of the order. One might want to speak of “low-level” phenomena or “high-level” concepts in the order, but one must recognize that the order relation itself does not determine a specific hierarchy of levels, although it does place limitations on the possible stratifications. My point is that there is often surprising flexibility in the nature of the level structure, as the example above shows even in a very simple case, and so what counts as low or high in terms of levels may be much less determined than one expects. In some of the linear gradings above, for example, the node $a$ could be described as high-level, and in others, it is low-level. Therefore if one wants to speak of levels for one’s order, then one must provide further elucidation of the stratification one has in mind.

Meanwhile, we often can provide a natural level structure. In the power set $P (X)$ of a finite set $X$ , ordered by the subset relation $A \subseteq B$ , for example, we can naturally stratify the relation by the sizes of the set, that is, in terms of the number of elements. Thus, we would place the $\emptyset$ on the bottom level, and the singleton sets ${a}$ on the next level, and then the doubletons ${a, b}$ , and so on. This stratification by cardinality doesn’t quite work when $X$ is infinite, however, since there can be instances of strict inclusion $A ⊊ B$ where $A$ and $B$ are both infinite and nevertheless equinumerous. Is there a level stratification of the infinite power set order?

Indeed there is, for every order relation admits a grading into levels.

Theorem. Every order relation $⟨ A, ≼ ⟩$ can be linearly graded. Indeed, every order relation can be extended to a linear order (not merely a preorder), and so it can be graded into levels with exactly one node on each level.

Proof. Let us begin with the finite case, which we prove by induction. Assume $≼$ is an order relation on a finite set $A$ . We seek to find a linear order $\leq$ on $A$ such that $x ≼ y ⟹ x \leq y$ . If $A$ has at most one element, then we are done immediately, since $≼$ would itself already be linear.

Let us proceed by induction. Assume that every order of size $n$ has a linear grading, and that we have a partial order $≼$ on a set $A$ of size $n + 1$ . Every finite order has at least one maximal element, so let $a \in A$ be a $≼$ -maximal element. If we consider the relation $≼$ on the remaining elements $A ∖ {a}$ , it is a partial order of size $n$ , and thus admits a linear grading order $\leq$ . We can now simply place $a$ atop that order, and this will be a linear grading of $⟨ A, ≼ ⟩$ , because $a$ was maximal, and so making it also greatest in the grading order will cohere with the grading condition.

So by induction, every finite partial order relation can be extended to a linear order.

Now, we consider the general case. Suppose that $≼$ is a partial order relation on a (possibly infinite) set $A$ . We construct a theory $T$ in a language with a new relation symbol $\leq$ and constant symbols $\dot{a}$ for every element $a \in A$ . The theory $T$ should assert that $\leq$ is a linear order, that $\dot{a} \leq \dot{b}$ , whenever it is actually true that $a ≼ b$ in the original order, and that $\dot{a} \neq \dot{b}$ whenever $a \neq b$ . So the theory $T$ describes the situation that we want, namely, a linear order that conforms with the original partial order.

The key observation is that every finite subset of the theory will be satisfiable, since such a finite subtheory in effect reduces to the case of finite orders, which we handled above. That is, if we take only finitely many of the axioms of $T$ , then it involves a finite partial order on the nodes that are mentioned, and by the finite case of the theorem, this order is refined by a linear order, which provides a model of the subtheory. So every finite subtheory of $T$ is satisfiable, and so by the compactness theorem, $T$ itself also is satisfiable.

Any model of $T$ provides a linear order $\leq$ on the constant symbols $\dot{a}$ , which will be a linear order extending the original order relation, as desired.

This material is adapted from my book-in-progress, Topics in Logic, which includes a chapter on relational logic, included an extended section on orders.

Universality, saturation and the surreal number line, Shanghai, June 2013

Posted on May 18, 2013 by Joel David Hamkins

Fudan bridge This will be a short lecture series given at the conclusion of the graduate logic class in the Mathematical Logic group at Fudan University in Shanghai, June 13, 18 (or 20), 2013.

I will present an elementary introduction to the theory of universal orders and relations and saturated structures. We’ll start with the classical fact, proved by Cantor, that the rational line is the universal countable linear order. But what about universal partial orders, universal graphs and other mathematical structures? Is there a computable universal partial order? What is the countable random graph? Which orders embed into the power set of the natural numbers under the subset relation $⟨ P (N), \subset ⟩$ ? Proceeding to larger and larger universal orders, we’ll eventually arrive at the surreal numbers and the hypnagogic digraph.

Fudan University seal

Joel David Hamkins

mathematics and philosophy of the infinite

Tag Archives: orders

Quantifer elimination

Endless dense linear orders

Theory of successor

Presburger arithmetic

Real-closed field

An algebra of orders

Linear gradings of partial orders

Universality, saturation and the surreal number line, Shanghai, June 2013

Endless dense linear orders

Theory of successor

Presburger arithmetic

Real-closed field

Share:

Share:

Share:

Share: