[bibtex key=HamkinsYang:SatisfactionIsNotAbsolute]
Abstract. We prove that the satisfaction relation
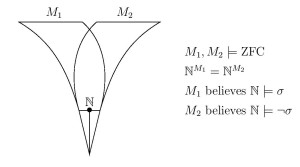
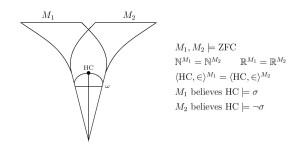
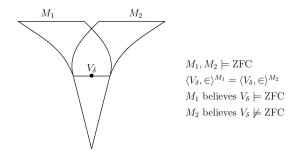
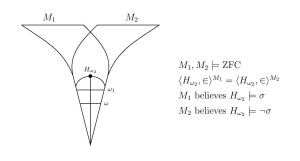
of first-order logic is not absolute between models of set theory having the structure N ⊧ 𝜑 [ ⃗ 𝑎 ] and the formulas N all in common. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic 𝜑 , yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and the same arithmetic truths, yet disagree on their truths-about-truth, at any desired level of the iterated truth-predicate hierarchy; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have the same ⟨ ℕ , + , ⋅ , 0 , 1 , < ⟩ or the same rank-initial segment ⟨ 𝐻 𝜔 2 , ∈ ⟩ , yet disagree on which assertions are true in these structures. ⟨ 𝑉 𝛿 , ∈ ⟩ On the basis of these mathematical results, we argue that a philosophical commitment to the determinateness of the theory of truth for a structure cannot be seen as a consequence solely of the determinateness of the structure in which that truth resides. The determinate nature of arithmetic truth, for example, is not a consequence of the determinate nature of the arithmetic structure
itself, but rather, we argue, is an additional higher-order commitment requiring its own analysis and justification. ℕ = { 0 , 1 , 2 , … }
 Many mathematicians and philosophers regard the natural numbers
Many mathematicians and philosophers regard the natural numbers
Feferman provides an instance of this perspective when he writes (Feferman 2013, Comments for EFI Workshop, p. 6-7) :
In my view, the conception [of the bare structure of the natural numbers] is completely clear, and thence all arithmetical statements are definite.
It is Feferman’s `thence’ to which we call attention. Martin makes a similar point (Martin, 2012, Completeness or incompleteness of basic mathematical concepts):
What I am suggesting is that the real reason for confidence in first-order completeness is our confidence in the full determinateness of the concept of the natural numbers.
Many mathematicians and philosophers seem to share this perspective. The truth of an arithmetic statement, to be sure, does seem to depend entirely on the structure
 Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as
Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as
We make our argument in part by proving that different models of set theory can have a structure identically in common, even the natural numbers, yet disagree on the theory of truth for that structure.
Theorem.
- Two models of set theory can have the same structure of arithmetic
⟨ ℕ , + , ⋅ , 0 , 1 , < ⟩ 𝑀 1 = ⟨ ℕ , + , ⋅ , 0 , 1 , < ⟩ 𝑀 2 , - Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is a well-order.
- Two models of set theory that have the same natural numbers and the same reals, yet disagree on projective truth.
- Two models of set theory can have a transitive rank initial segment in common
⟨ 𝑉 𝛿 , ∈ ⟩ 𝑀 1 = ⟨ 𝑉 𝛿 , ∈ ⟩ 𝑀 2 ,
 The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.
The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.