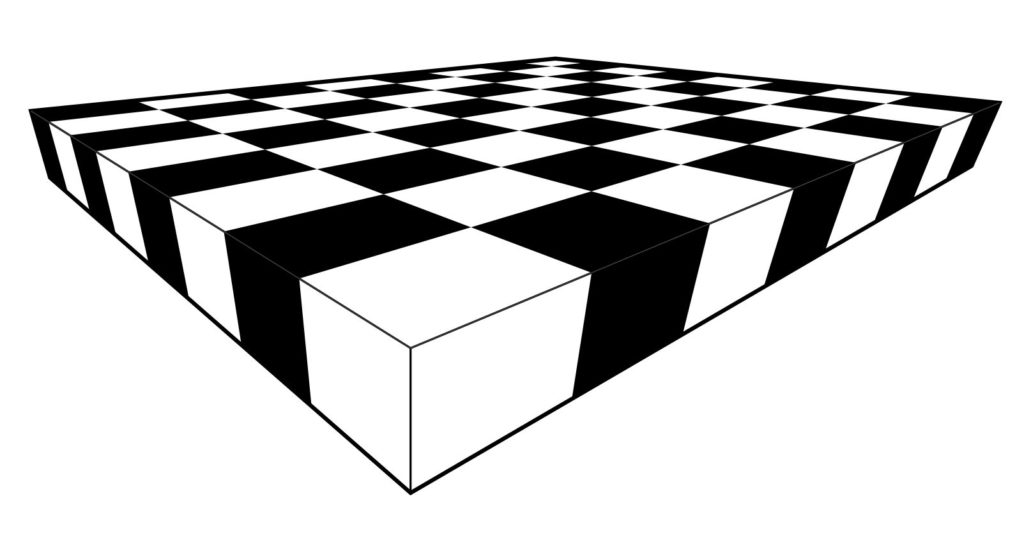
Let me show you how to hand-draw an image of a chessboard in perspective, using only a straightedge. There is no need to measure any distances or to make calculations of any kind.  All you need is a straightedge, paper and your pen or pencil.

Imagine the vast doodling potential!  A person who happens to be stuck in a lecture on some other less interesting topic could easily make one or more elaborate chessboards in perfect perspective, using only a straightedge! Please carry out the construction and then share your resulting images. I would love to see them.

To begin, give yourself a horizon at the top of the page, with two points at infinity (in orange), and also two points (blue) that will become the front and back corner of your chessboard.  You can play around with different arrangements of these points, which will lead ultimately to different perspective views.

Using your straightedge, draw the lines from those reference points to the points at infinity. The resulting enclosed region will ultimately become the main chess board. One can alternatively think of starting with the front edges of the desired board, and then setting a horizon and using that to determine the points at infinity, and then adding the back edges. If you like, you can add a third point at infinity down below, and a front bottom reference point (blue), to give the board some thickness. Construct the lines to the bottom point at infinity.

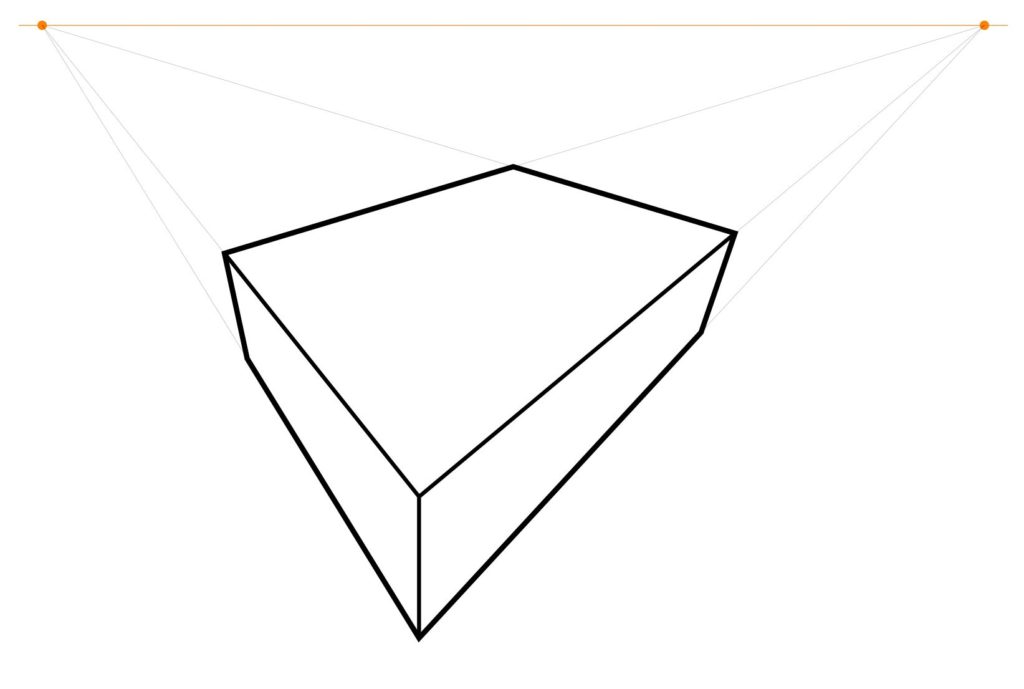
The result is now the main outline of your chessboard as a rectangular solid.

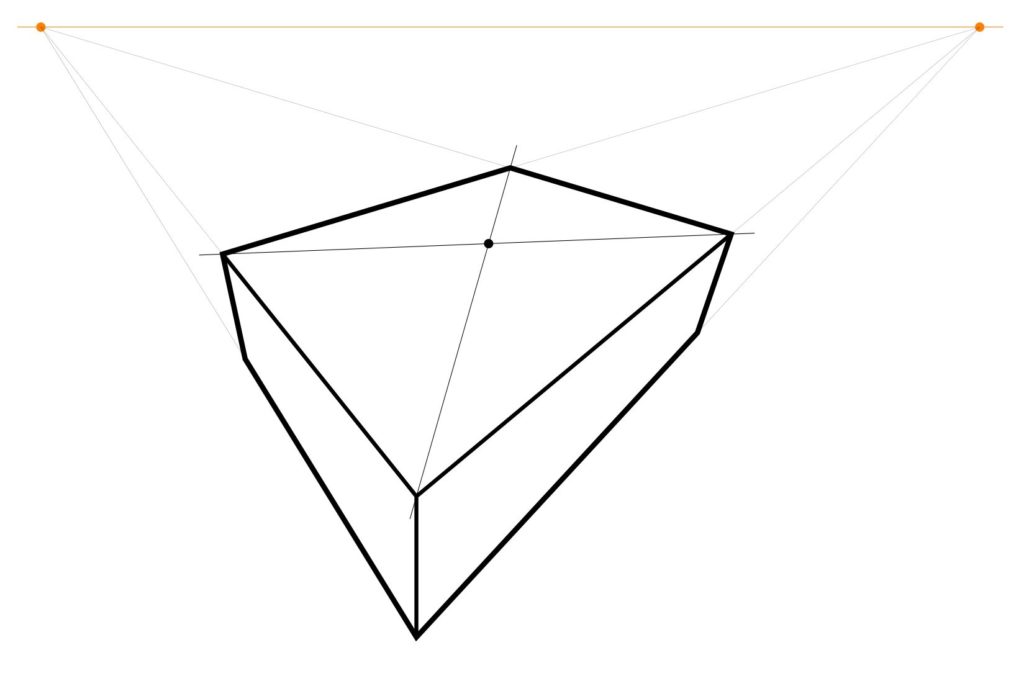
Next, construct the center point of the top face, by drawing the two diagonals and finding the intersection point. I call this the center point, because it is the point that represents in the perspective view the actual center point of the chessboard, even though this point is not in the “center” of the quadrilateral representing the board. It is remarkable that one can find that point without needing to measure or calculate anything, simply because the two straight lines of the diagonal of the chessboard intersect at that point, and this remains true in the perspective view. This is the key idea that enables the entire construction method to proceed with only a straightedge.

Construct the midpoint lines by drawing the lines from that centerpoint to the points at infinity.

Now you have the chessboard with the main midlines drawn.

Construct the center points of the two diagonal squares, by intersecting the diagonals of each of them.

Construct the lines that extend those points to the points at infinity.

Thus, you have constructed the main 4 x 4 grid.

You can extend the grid lines down to the bottom point at infinity like so:

One can stop with the 4 x 4 board, if desired. Simply add suitable shading, and you’ve completed the 4 x 4 chessboard in perspective.

Alternatively, one can continue with one more iteration to construct the 8 x 8 board. From the 4 x 4 grid (with no shading yet) simply construct the center points of the squares on the main diagonal, and extend those lines to infinity.  This will enable you to draw the 8 x 8 grid lines, and after shading, you’ll have the complete chessboard.

The initial arrangement of points affects the nature of the perspective view. Having the points at infinity very far away will produce something closer to orthoprojection; having them close produces a more extreme perspective, which simulates a view from a vantage point extremely close to the board.

Please give the construction a try! All you need is paper, pencil and a straightedge! Provide links below in the comments to photos of your creations.

Meanwhile, let me point you towards my follow post, How to draw infinite chessboards by hand in perfect perspective, using only a straightedge. The difference between the methods is that the method of this post is about subdividing a given board, and the other method is about generating arbitrarily large chessboards from a given unit square.

I learned these construction method years ago from my CUNY geometer colleague Ilya Kofman.