This will be a talk for the CUNY Set Theory Seminar, March 6, 2015.

I shall describe the current state of knowledge concerning the question of whether there can be an embedding of the set-theoretic universe into the constructible universe.

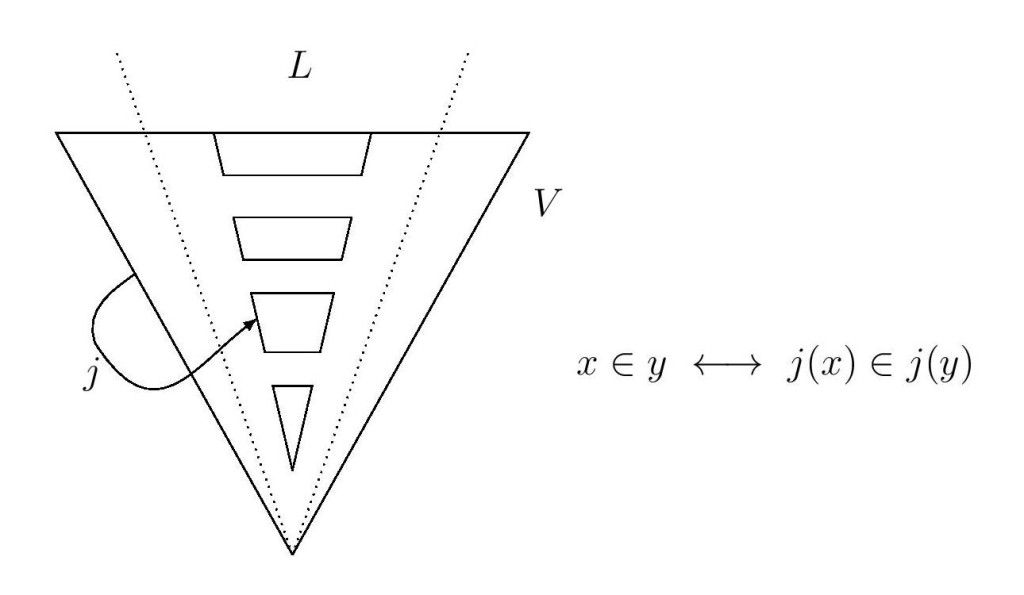
Question.(Hamkins) Can there be an embedding $j:V\to L$ of the set-theoretic universe $V$ into the constructible universe $L$, when $V\ne L$?

The notion of embedding here is merely that $$x\in y⟺j(x)\in j(y),$$ and such a map need not be elementary nor even ${\mathrm{\Delta }}_0$-elementary. It is not difficult to see that there can generally be no ${\mathrm{\Delta }}_0$-elementary embedding $j:V\to L$, when $V\ne L$.

Nevertheless, the question arises very naturally in the context of my previous work on the embeddability phenomenon, Every countable model of set theory embeds into its own constructible universe, where the title theorem is the following.

Theorem.(Hamkins) Every countable model of set theory $⟨M,{\in }^M⟩$, including every countable transitive model of set theory, has an embedding $j:⟨M,{\in }^M⟩\to ⟨L^M,{\in }^M⟩$ into its own constructible universe.

The methods of proof also established that the countable models of set theory are linearly pre-ordered by embeddability: given any two models, one of them embeds into the other; or equivalently, one of them is isomorphic to a submodel of the other. Indeed, one model $⟨M,{\in }^M⟩$ embeds into another $⟨N,{\in }^N⟩$ just in case the ordinals of the first ${\text{Ord}}^M$ order-embed into the ordinals of the second ${\text{Ord}}^N$. (And this implies the theorem above.)

In the proof of that theorem, the embeddings $j:M\to L^M$ are defined completely externally to $M$, and so it was natural to wonder to what extent such an embedding might be accessible inside $M$. And I realized that I could not generally refute the possibility that such a $j$ might even be a class in $M$.

Currently, the question remains open, but we have some partial progress, and have settled it in a number of cases, including the following, on which I’ll speak:

• If there is an embedding $j:V\to L$, then for a proper class club of cardinals $\lambda$, we have $(2^{\lambda }{)}^V=({\lambda }^{+}{)}^L$.
• If $0^{\mathrm{♯}}$ exists, then there is no embedding $j:V\to L$.
• If $0^{\mathrm{♯}}$ exists, then there is no embedding $j:V\to L$ and indeed no embedding $j:P(\omega )\to L$.
• If there is an embedding $j:V\to L$, then the GCH holds above ${\mathrm{\aleph }}_0$.
• In the forcing extension $V[G]$ obtained by adding ${\omega }_1$ many Cohen reals (or more), there is no embedding $j:V[G]\to L$, and indeed, no $j:P(\omega {)}^{V[G]}\to V$. More generally, after adding ${\kappa }^{+}$ many Cohen subsets to $\kappa$, for any regular cardinal $\kappa$, then in $V[G]$ there is no $j:P(\kappa )\to V$.
• If $V$ is a nontrivial set-forcing extension of an inner model $M$, then there is no embedding $j:V\to M$. Indeed, there is no embedding $j:P({\kappa }^{+})\to M$, if the forcing has size $\kappa$. In particular, if $V$ is a nontrivial forcing extension, then there is no embedding $j:V\to L$.
• Every countable set $A$ has an embedding $j:A\to L$.

This is joint work of myself, W. Hugh Woodin, Menachem Magidor, with contributions also by David Aspero, Ralf Schindler and Yair Hayut.

See my related MathOverflow question: Can there be an embedding $j:V\to L$ from the set-theoretic universe $V$ to the constructible universe $L$, when $V\ne L$?

Talk Abstract