I should like to follow up my post last week about the impossibility of finding regular polygons in the integer lattice. This time, however, we shall consider the hexagonal and triangular lattices.  It is easy to find lattice points that form the vertices of an equilateral triangle or a regular hexagon.

And similarly, such figures can be found also in the triangular lattice.

Indeed, the triangular and hexagonal lattices are each refinements of the other, so they will allow exactly the same shapes arising from lattice points.

But can you find a square? How about an octagon?

Question.  Which regular polygons can be formed by vertices of the hexagonal or triangular lattices?

The answer is that in fact there are no other types of regular polygons to be found! I’d like to prove this by means of some elementary classical reasoning.

Theorem. The only non-degenerate regular polygons that arise from vertices in the hexagonal or triangular lattices are the equilateral triangles and regular hexagons.

This theorem extends the analysis I gave in my post last week for the integer lattice, showing that there are no regular polygons in the integer lattice, except squares.

Proof.  The argument for the hexagonal and triangular lattices uses a similar idea as with the integer lattice, but there is a little issue with the square and pentagon case. We can handle both the hexagonal and triangular lattices at the same time. The crucial fact is that both of these lattices are invariant by ${120}^{\circ }$ rotation about any lattice vertex.

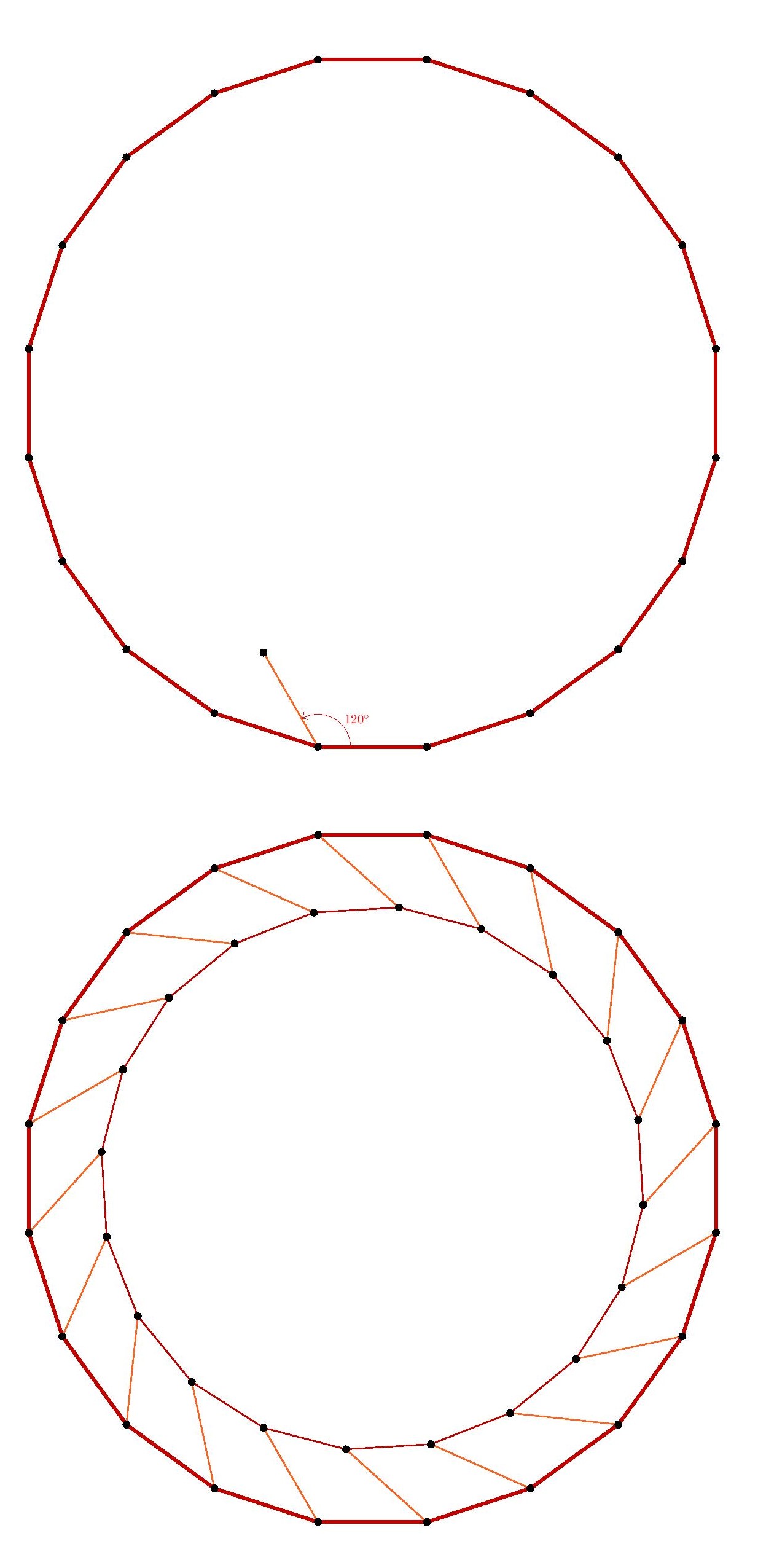
To get started, suppose that we can find a square in the hexagonal lattice. 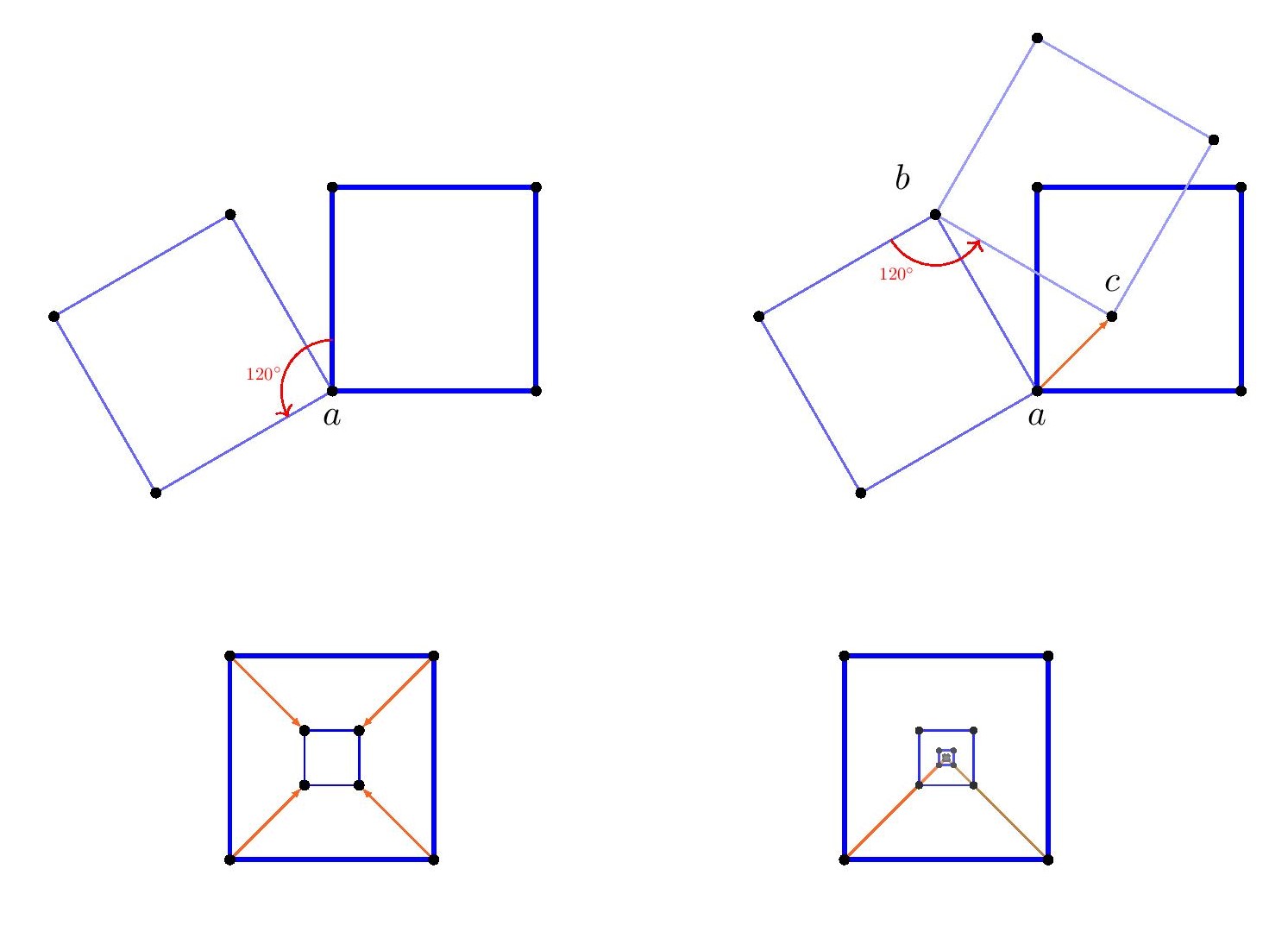 We may rotate this square by ${120}^{\circ }$ about the vertex $a$, and the square vertices will all land on lattice-vertex points. Next, we may rotate the resulting square about the point $b$, and again the vertices will land on lattice points. So we have described how to transform any square vertex point $a$ to another lattice point $c$ which is strictly inside the square. By applying that operation to each of the four vertices of the square, we thereby arrive by symmetry at a strictly smaller square. Thus, for any square in the hexagonal or triangular lattice, there is a strictly smaller square. But if there were any square in the lattice at all, there would have to be a square with smallest side-length, since there are only finitely many lattice distances less than any given length. So there can be no square in the hexagonal or triangular lattice.

The same construction works with pentagons.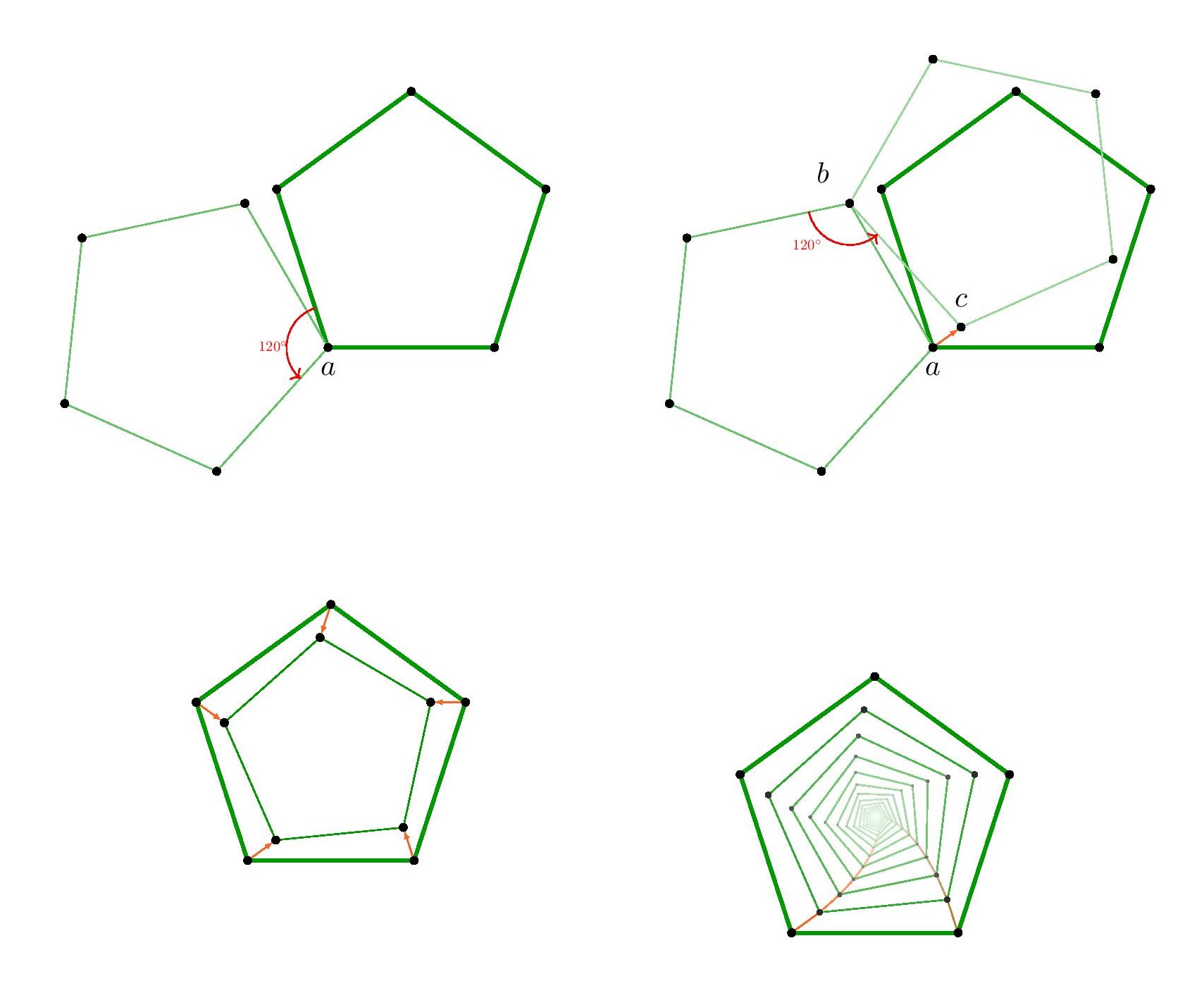 

If there is a pentagon in the lattice, then we may rotate it about point $a$, and then again about point $b$, resulting in point $c$ strictly inside the pentagon, which leads to an infinite sequence of strictly smaller pentagon, whose sizes (by similarity) go to zero. So there can be no pentagon in the hexagonal or triangular lattices.

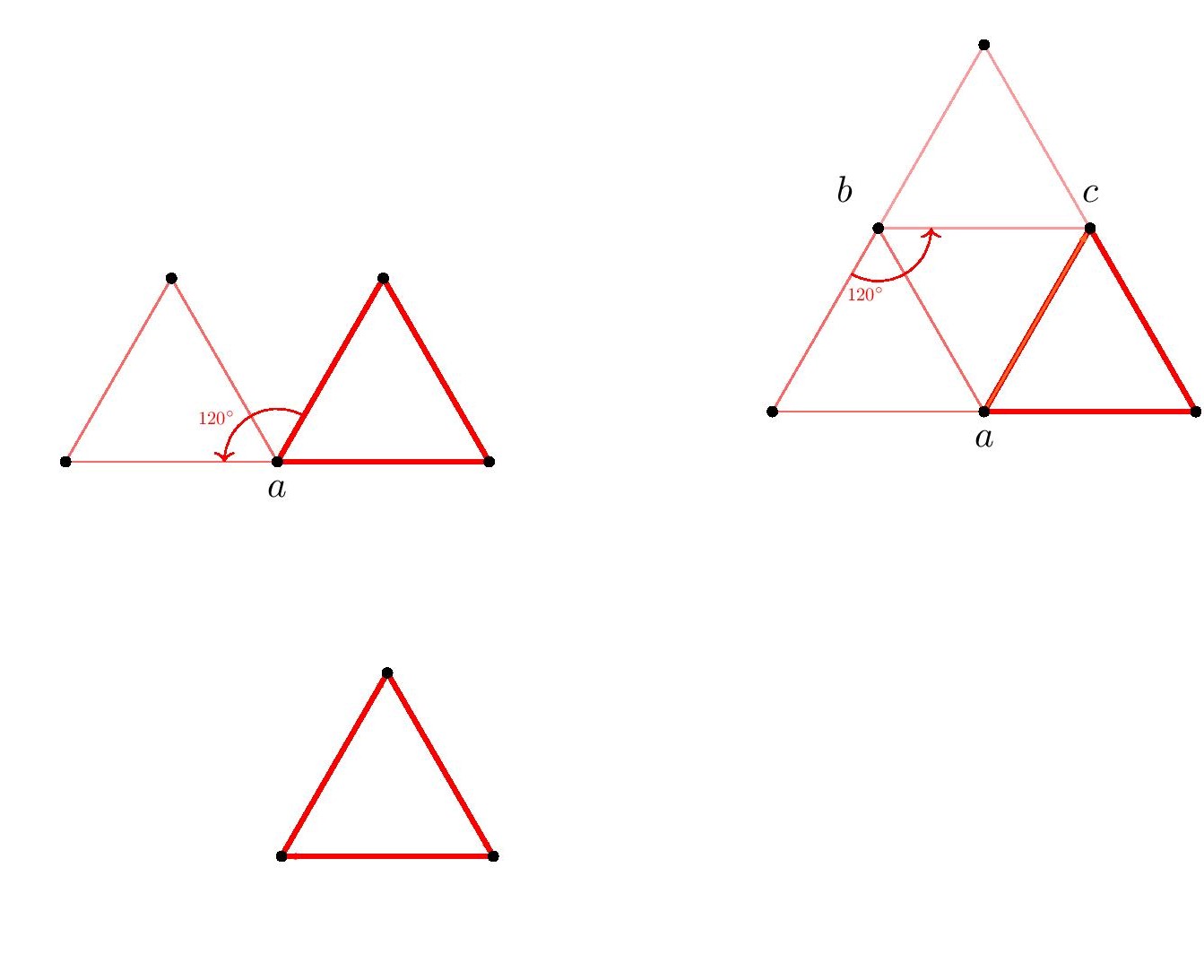
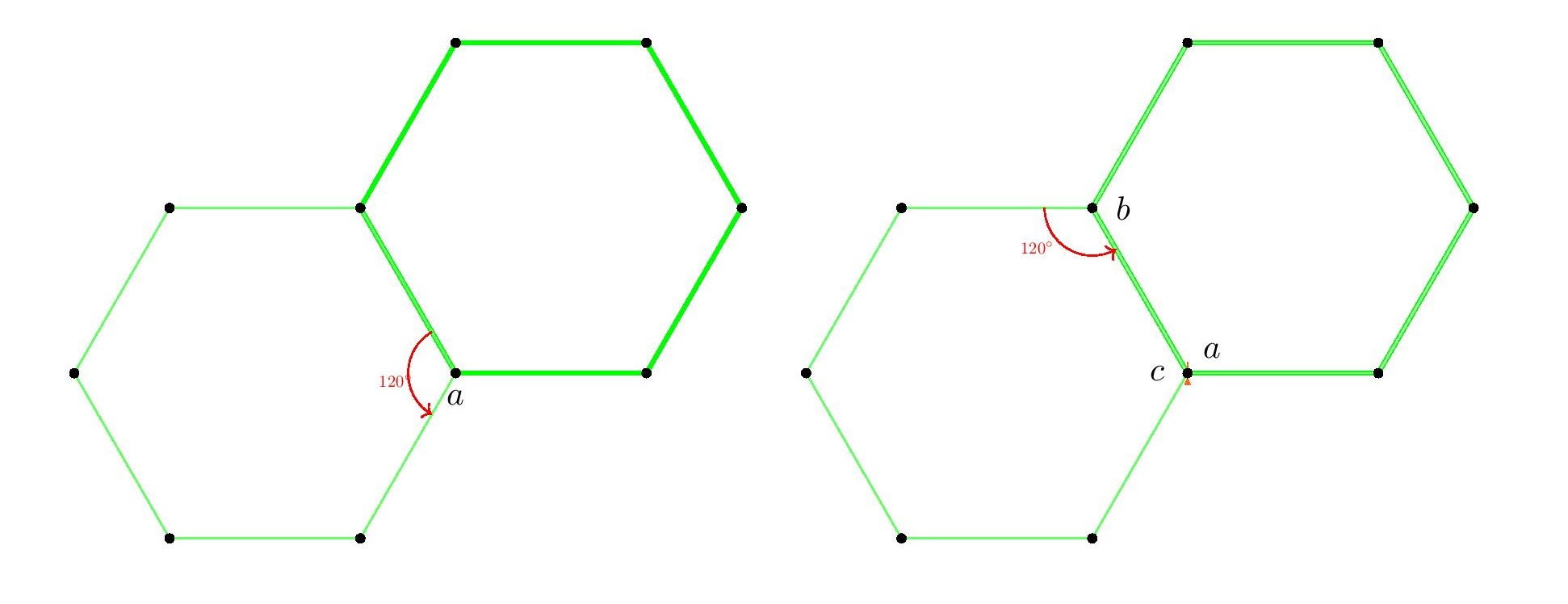
If we attempt to apply this argument with triangles or hexagons, then the process simply leads back again to points in the original figure. But of course, since triangles and hexagons do arise in these grids, we didn’t expect the construction to work with them.

 

 

 

 

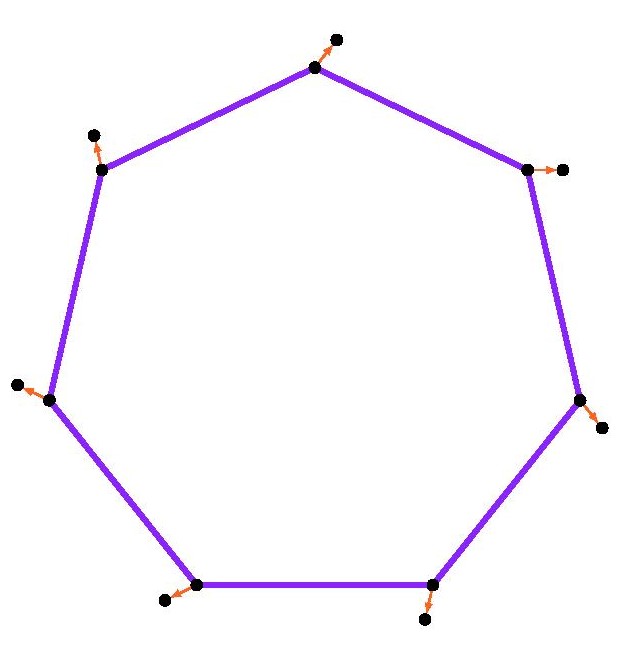
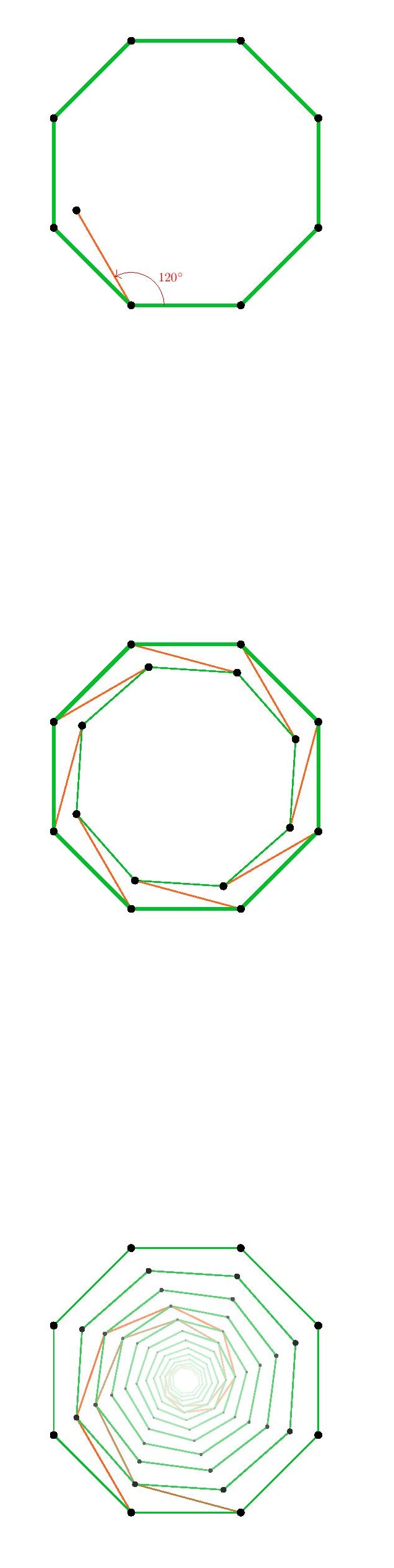
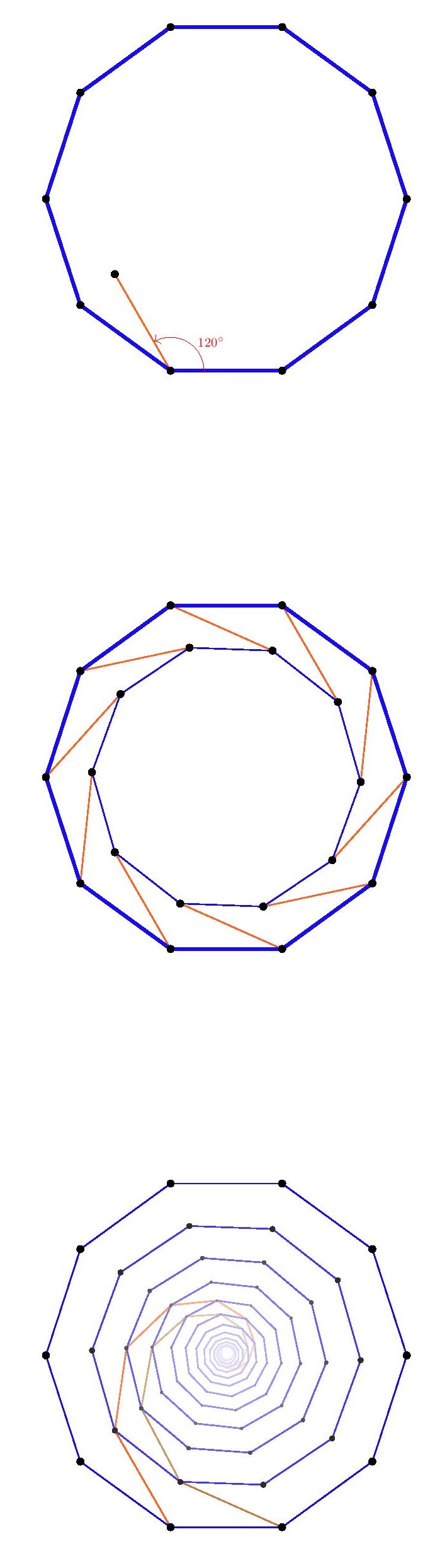
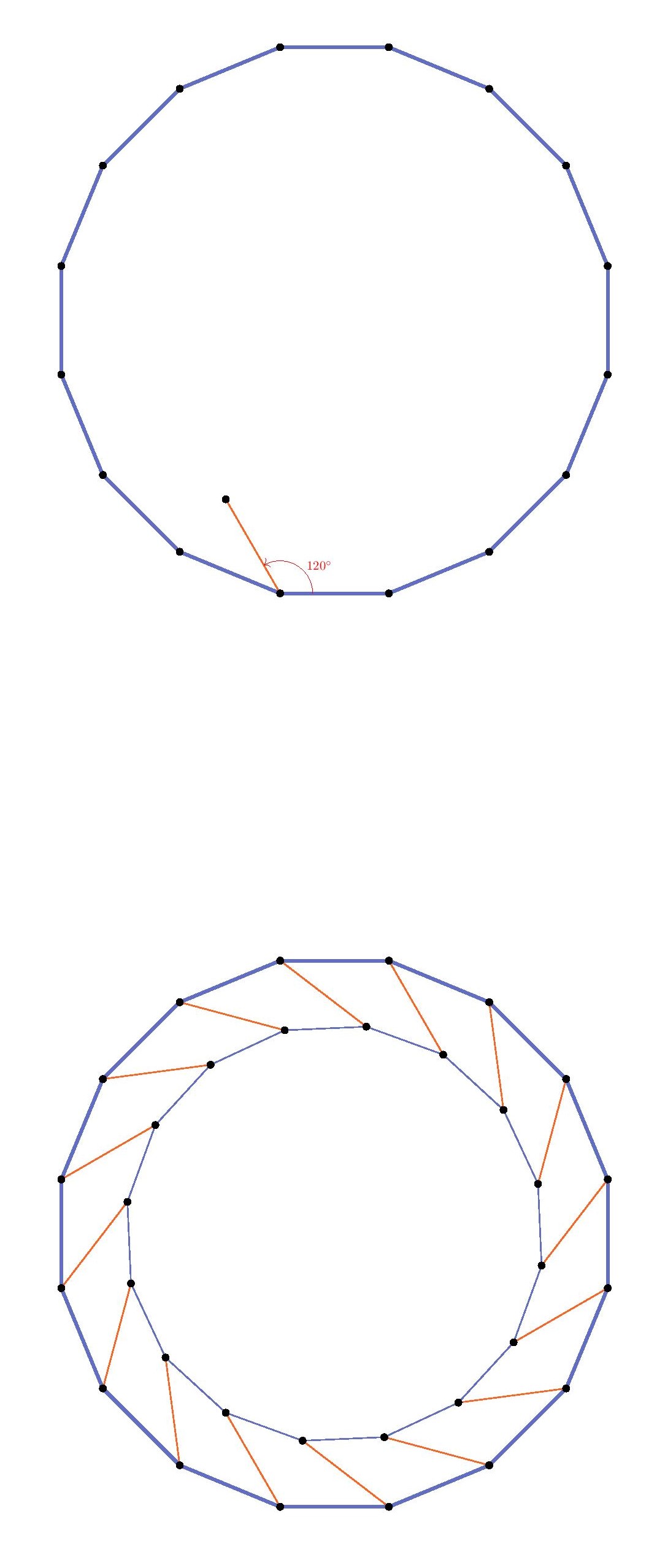
But also, this particular two-step rotation construction does not succeed with the heptagon (7-sides) or larger polygons, since the resulting point $c$ ends up outside the original heptagon, which means that the new heptagon we construct ends up being larger, rather than smaller than the original.

 

 

 

 

 

 

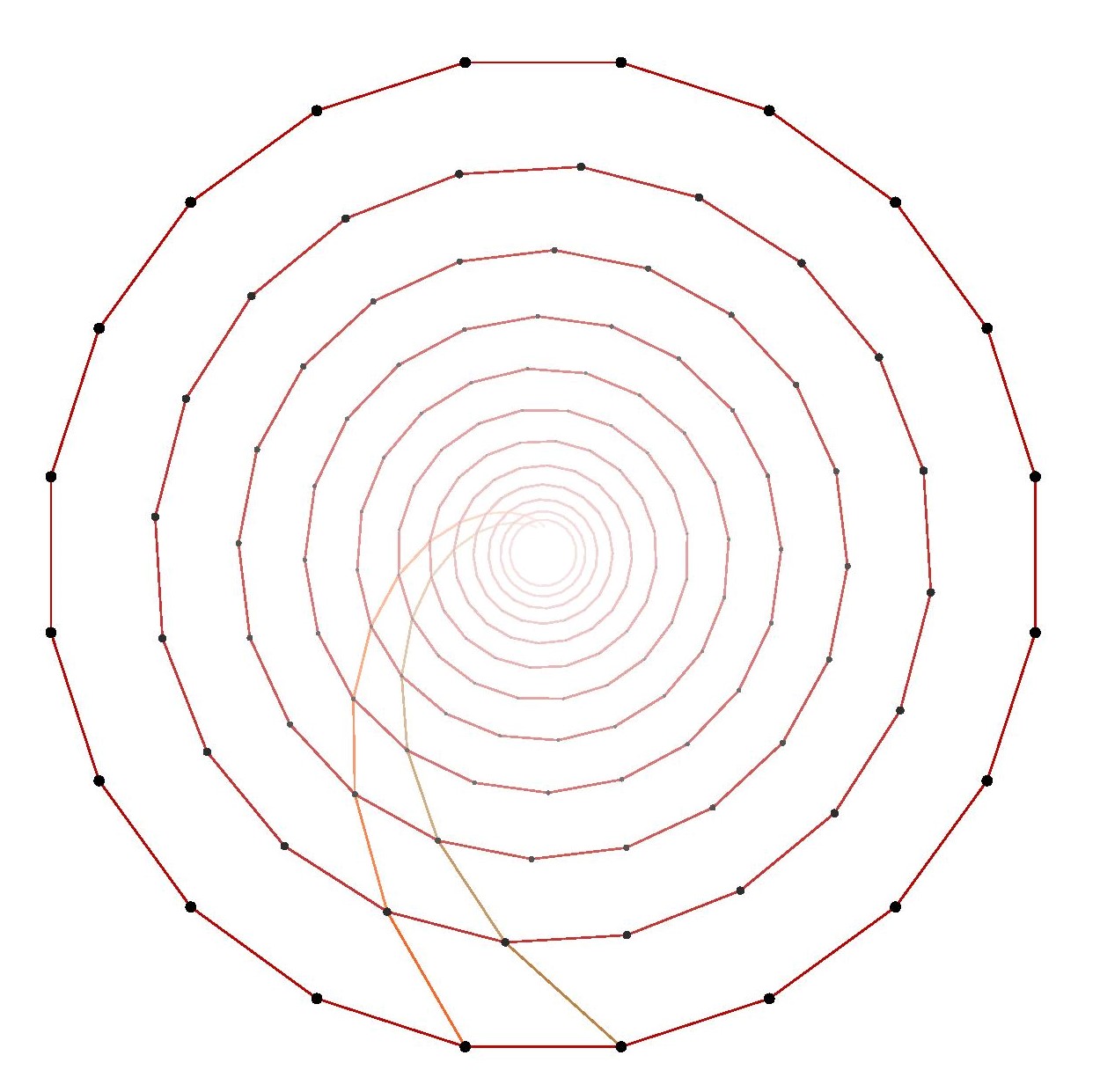
Fortunately, for the 7-gon and higher, we may fall back on the essential idea used in the square lattice case. Namely, because the interior angles of these polygons are now larger than ${120}^{\circ }$, we may simply rotate each side of the polygon by ${120}^{\circ }$ and thereby land at a lattice point. In this way, we construct a proportionally smaller instance of the same regular $n$-gon, and so there can be no smallest instance of such a polygon.

 

In summary, in every case of a regular polygon except the equilateral triangle and the regular hexagon, we found that by means of ${120}^{\circ }$ rotations we were able to find a strictly smaller instance of the polygon. Therefore, there can be no instances of such polygons arising from lattice points in the hexagonal or triangular tilings. QED

See my earlier post: there are no regular polygons in the integer lattice, except squares.