Consider a regular square lattice, formed by a grid of intersection points of uniformly spaced parallel horizontal and vertical lines in the plane. One may easily find points that form the vertices of a square in this lattice.
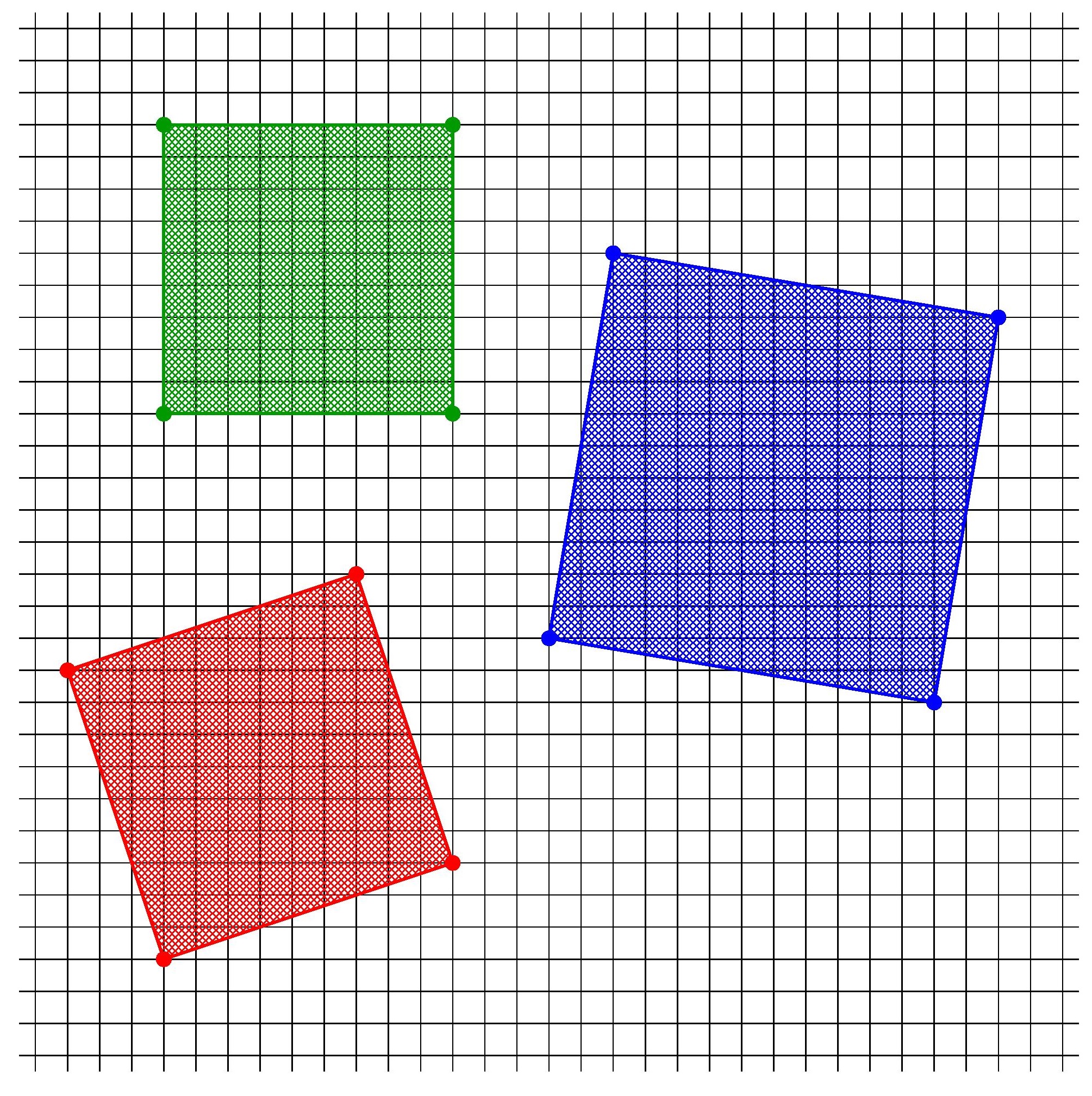
But can one find points that form the vertices of regular hexagon? Or a regular pentagon? How about an equilateral triangle? And so on.
The answer is that one cannot find these shapes using vertices in the square lattice.
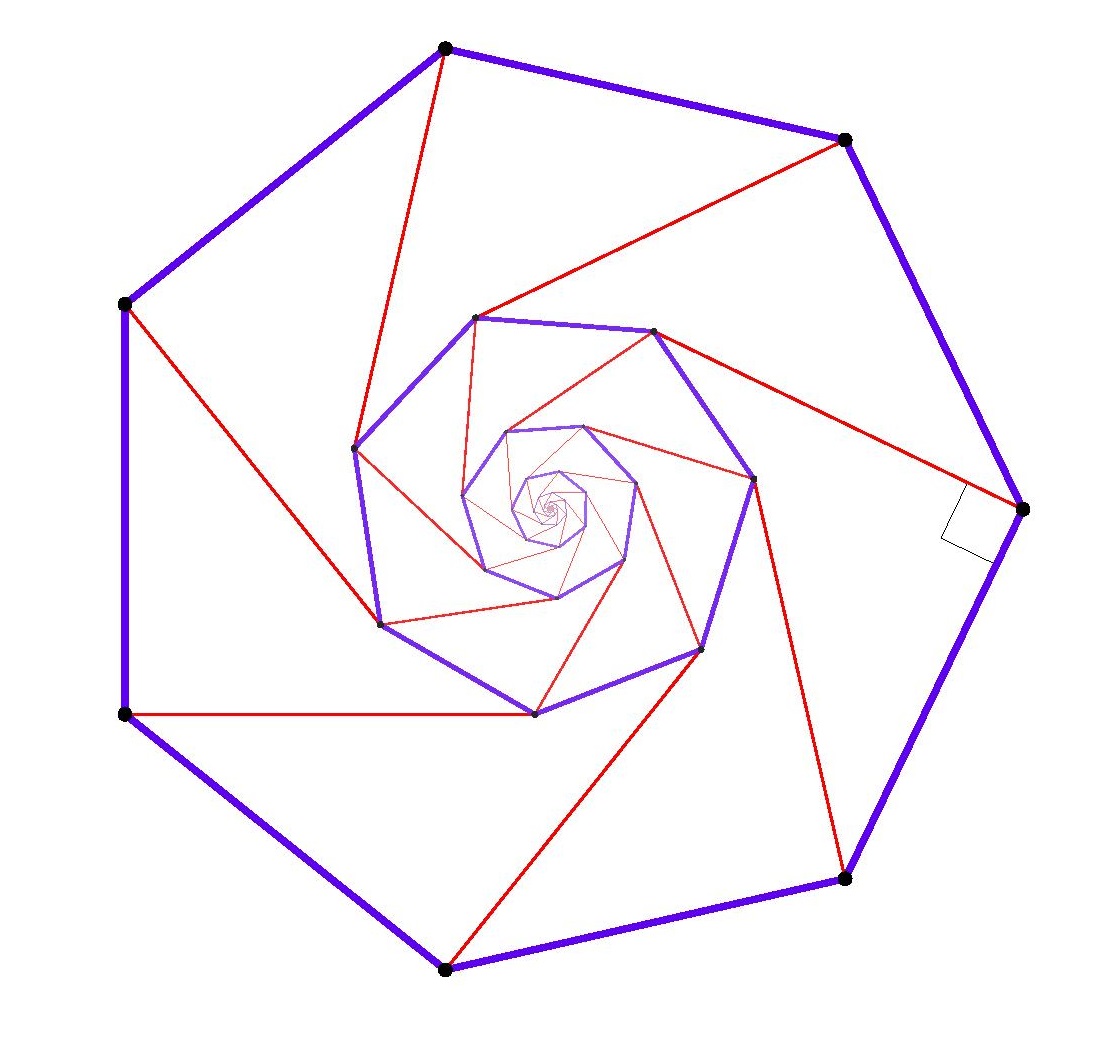
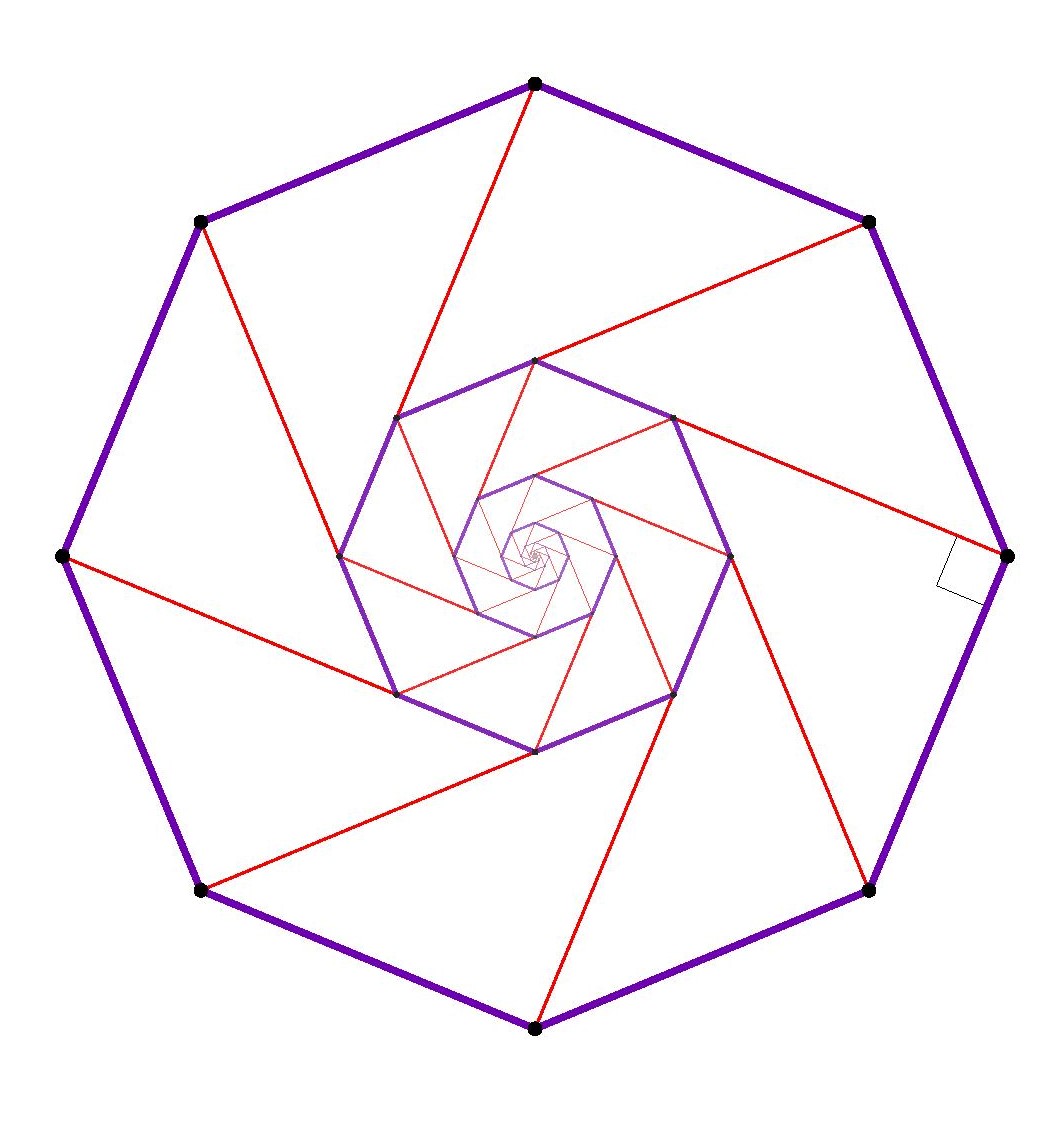
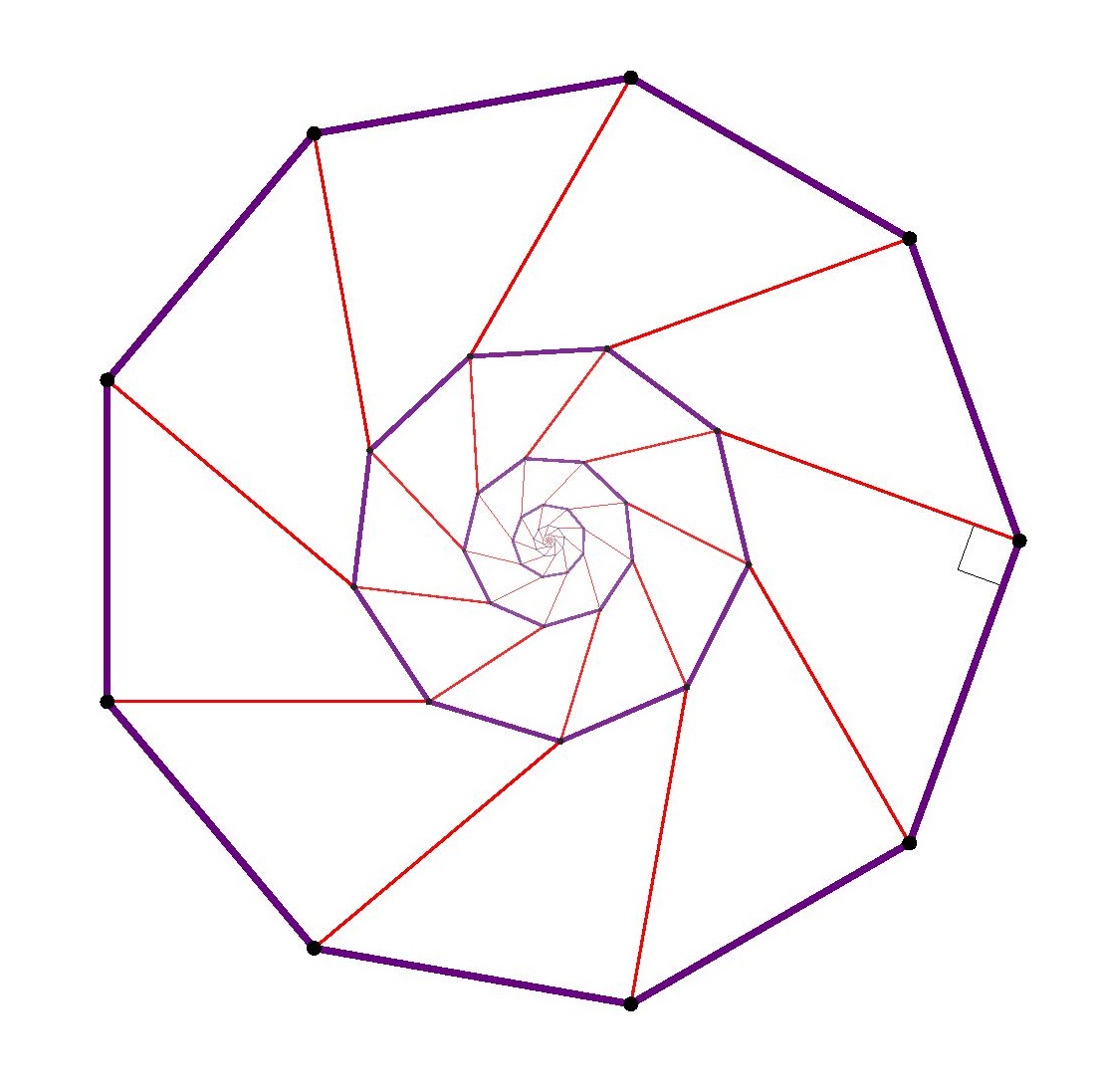
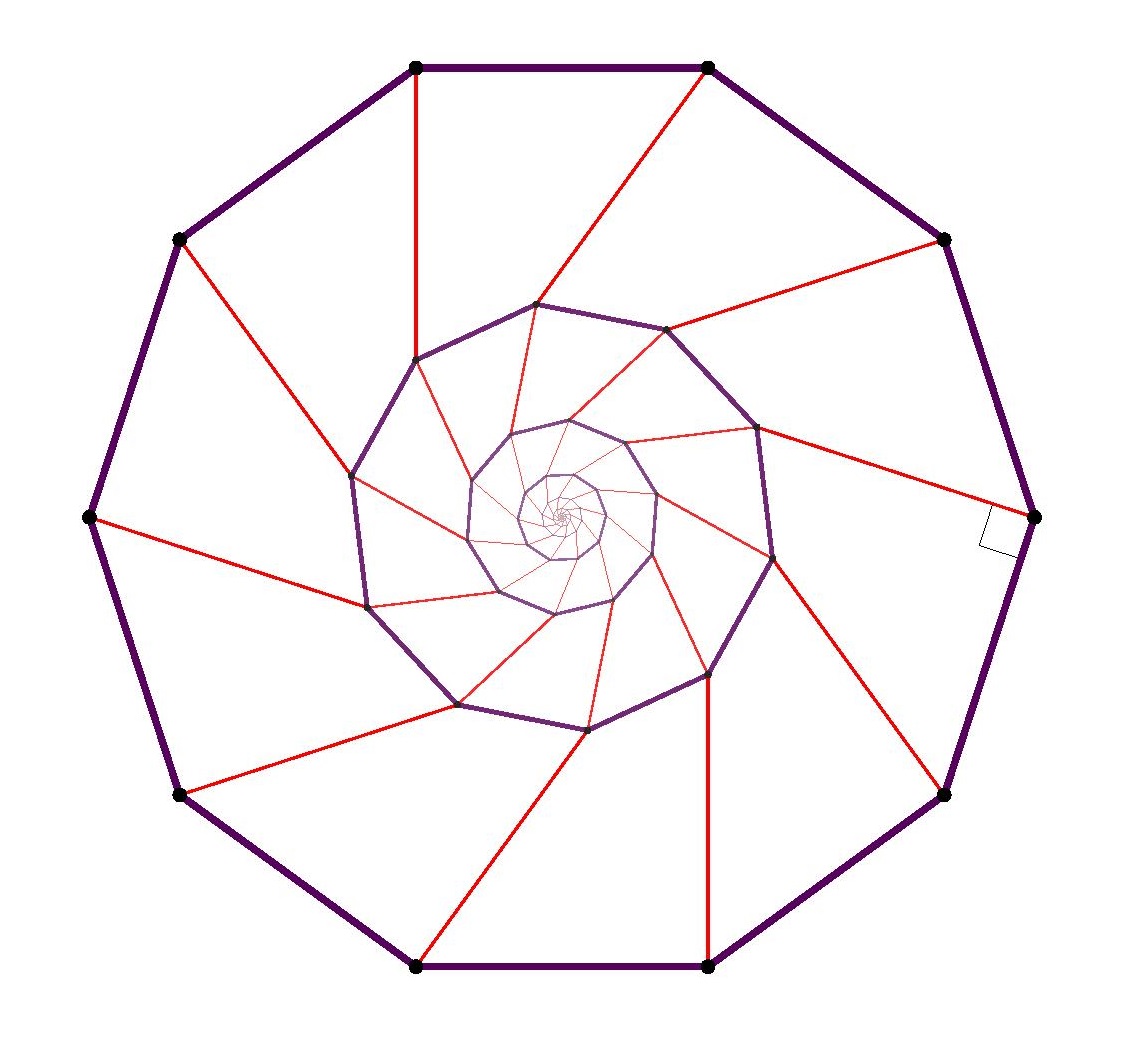
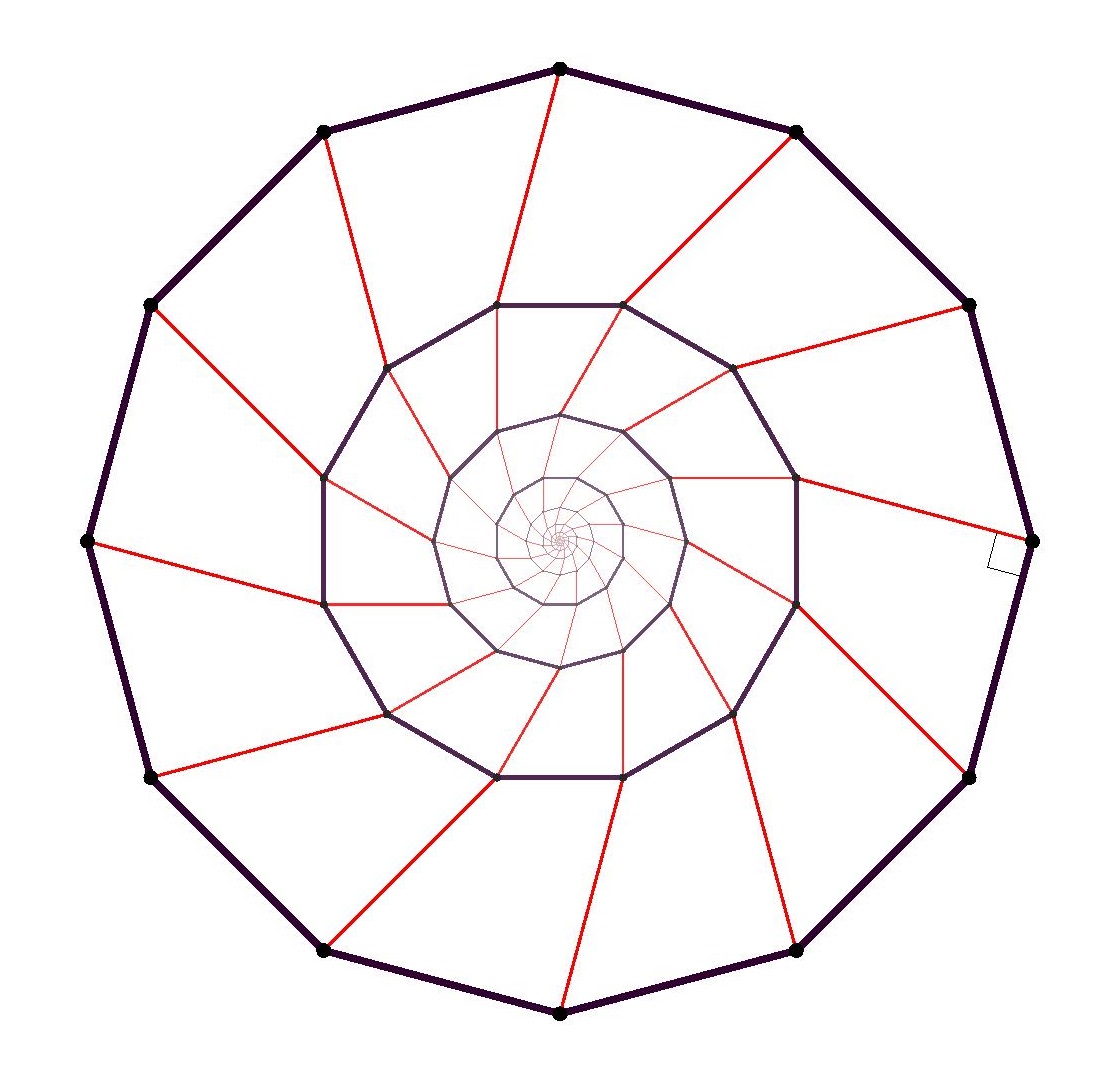
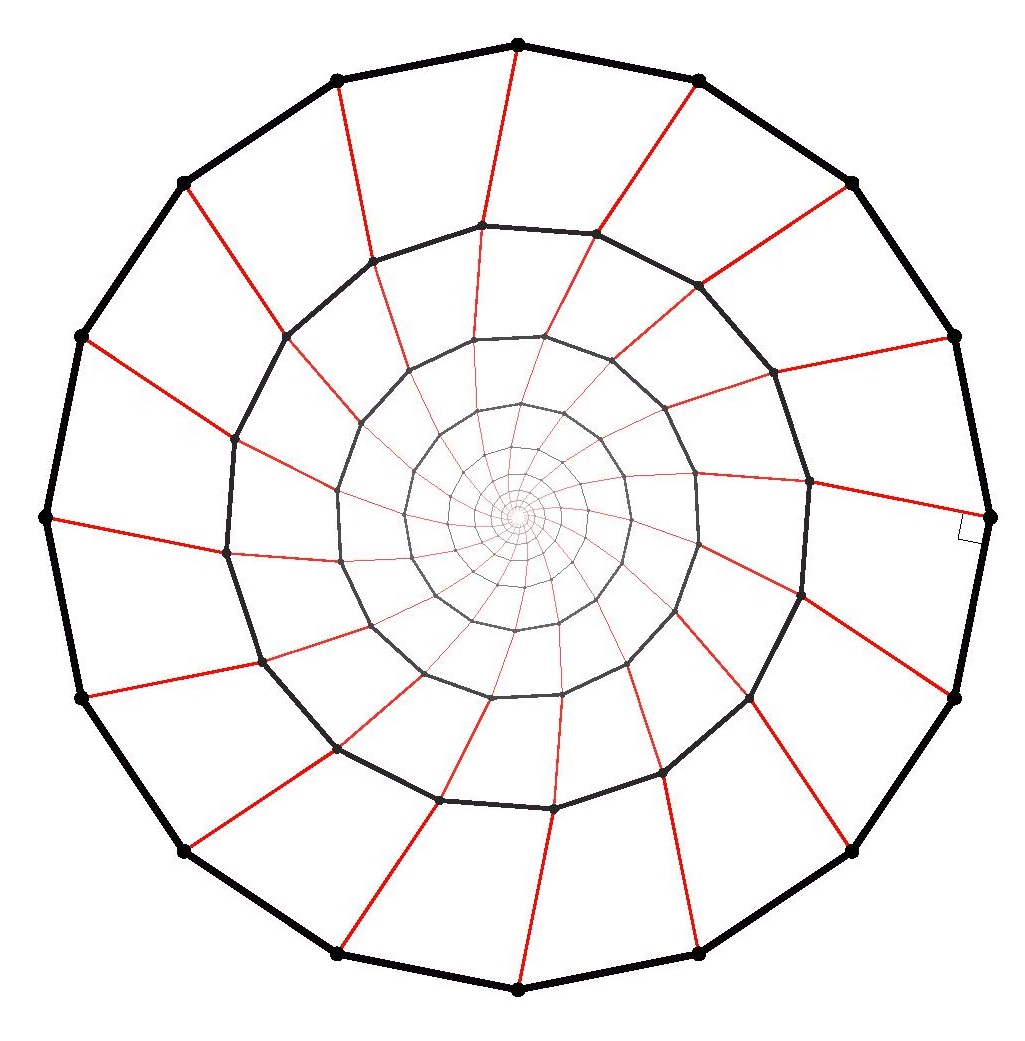
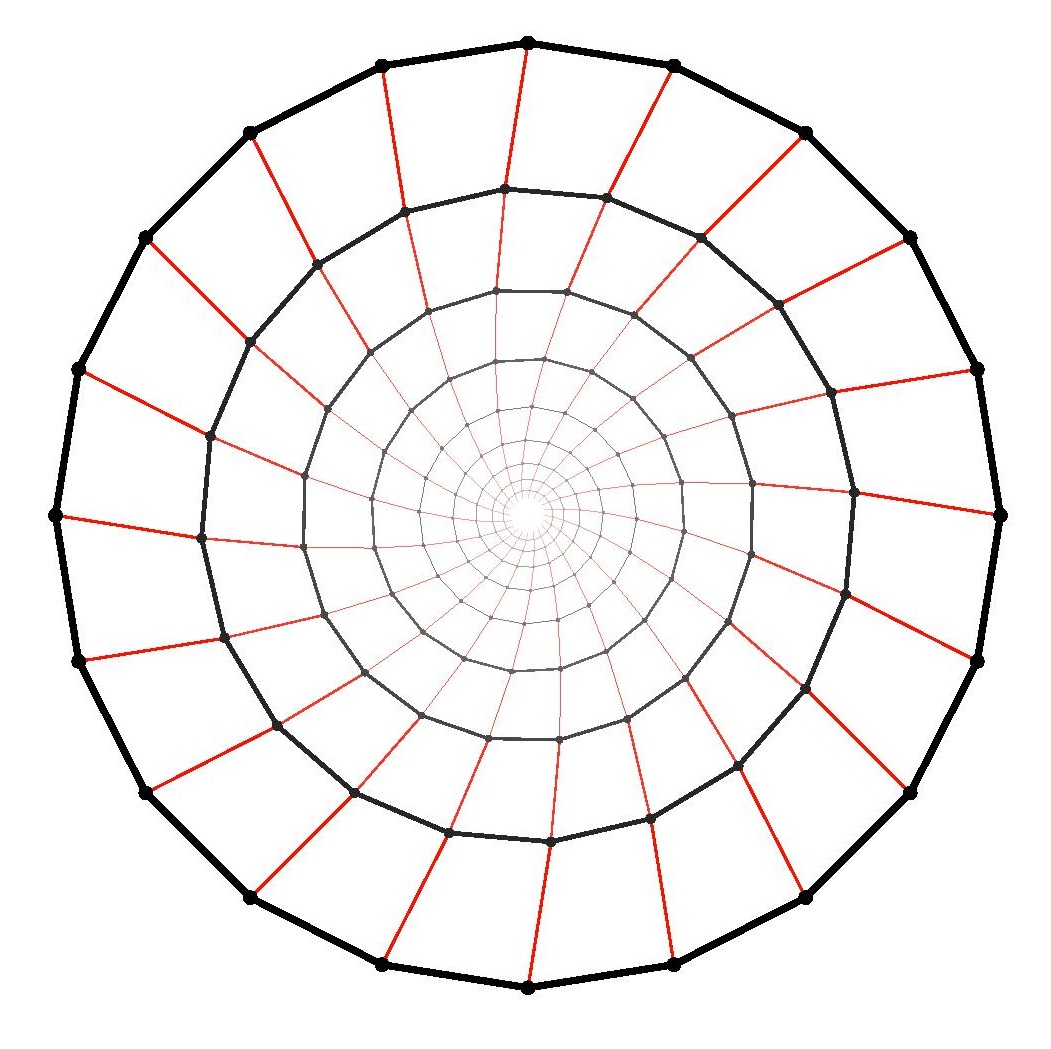
Theorem. There is no regular pentagon in the square lattice, and no regular hexagon, no regular heptagon, and so on. Indeed, the only nondegenerate regular polygons to be found using vertices in a square lattice are squares themselves.
I think this must be a classical result. I was inspired by Vaughn Climenhaga’s beautiful image in his Proof without words answer on MathOverflow, which handled the case of a hexagon. Reflecting upon it, I realized that the same idea works with other regular polygons, and I endeavored to produce the corresponding images, below.
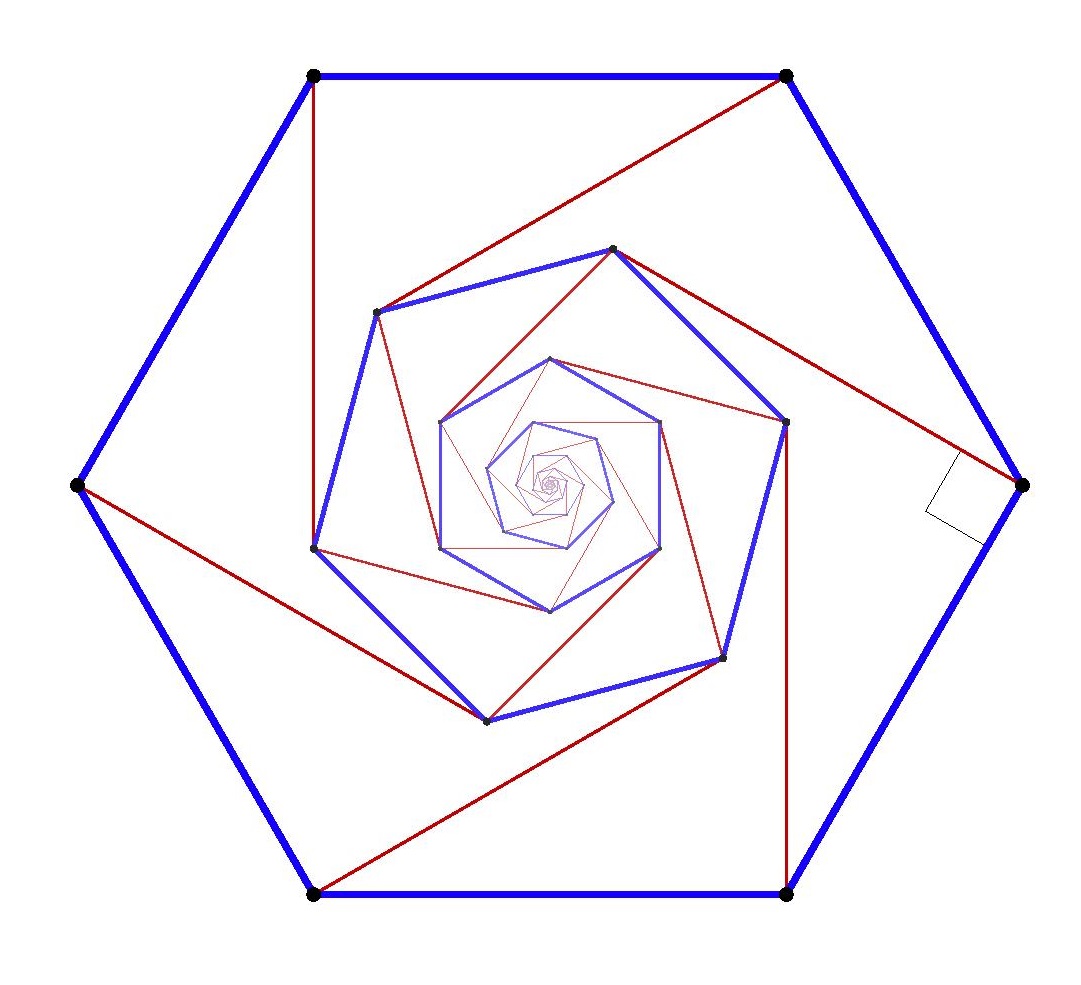
Proof. Suppose that we could find five vertices in the square lattice that formed a regular pentagon. Construct on each side a perpendicular of the same length, as pictured in brown below. Since the lattice is invariant under 
An alternative way to argue is: by similarity, the size of the smaller pentagon shrinks by the same factor with each step, and so in the limit the size approaches zero; but clearly, we cannot have a lattice-point regular pentagon whose size is smaller than the square lattice spacing itself. So there is no regular pentagon in the square lattice.
The same argument works with larger regular polygons. The main point to realize is that for all regular
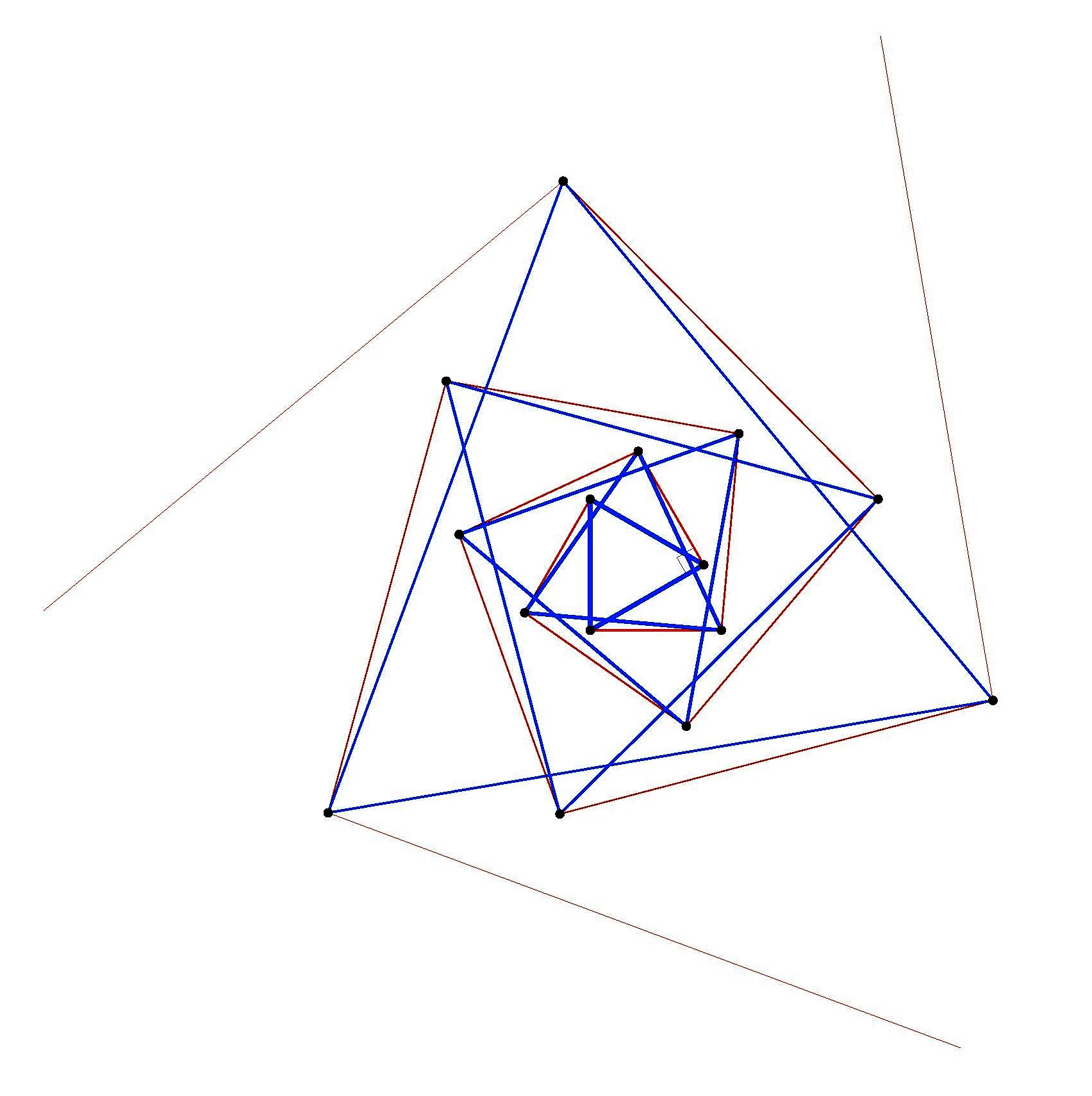
The case of an equilateral triangle requires special care. If one attempts the same construction idea as above, building the perpendicular on the edges of a triangle, then the resulting triangle becomes larger, rather than smaller, and so the proof method breaks down.
Nevertheless, one can reduce the equilateral triangle case to a hexagon: if you could find an equilateral triangle in the square lattice, then since the lattice is invariant under translation via a lattice-point line segment, it follows that we could build a regular hexagon. But we have already showed that we cannot find a regular hexagon in the square lattice, and so we cannot find an equilateral triangle.

So we’ve completed the proof for all nondegenerate regular polygons, except the square. QED
For those who might be interested, here is the tex code I used to generate the nested polygons. The code accepts input
\documentclass{minimal}
\usepackage[rgb]{xcolor}
\usepackage{tikz}
\usetikzlibrary{positioning,calc}
\usepackage{ifthen}
\begin{document}
\newcommand\nestedpolygon[1]{
\begin{tikzpicture}[scale=4]
\pgfmathsetmacro\n{#1}
\pgfmathsetmacro\m{\n-1}
\pgfmathsetmacro\shrink{sqrt((sin(180/\n))^2+(cos(180/\n)-2*sin(180/\n))^2)}
\pgfmathsetmacro\OffSet{acos((sin(180/\n)^2+cos(180/\n)*(cos(180/\n)-2*sin(180/\n)))/\shrink)}
\pgfmathsetmacro\gc{360+100*exp((5-\n)/3.5)}
\pgfmathsetmacro\gcc{640+120*exp((5-\n)/3)}
\definecolor{GonColor}{wave}{\gc}
\definecolor{GonColorC}{wave}{\gcc}
\pgfmathsetmacro\d{8}
\foreach \k in {0,...,\d} {
\pgfmathsetmacro\R{\shrink^\k};
\pgfmathsetmacro\c{100*exp(-\k/6)};
\pgfmathsetmacro\a{2*\R*sin(180/\n)}
\pgfmathsetmacro\f{\k*\OffSet}
\foreach \i in {0,...,\m} {
\coordinate (x) at (360*\i/\n+\f:\R);
\coordinate (y) at (360*\i/\n+360/\n+\f:\R);
% the perp indicator
\ifthenelse{\k=0\AND\i=\m\AND\n<20}{\draw[very thin,black!\c!white] ($(x)!.85!(y)$) node (p) {} --
($(p)!1!90:(y)$) node (q) {} -- ($(q)!1!90:(p)$);}{}
% connecting to lower level
\draw [line width=.5*exp(-\k/2),GonColorC!\c!white] (y) -- ($(y)!1!-90:(x)$);
% edge and vertices of current gon
\draw [line width=1.5*exp(-\k/2),GonColor!\c!white] (x) node
[circle,scale=.3*\R,black!\c!white,fill=black!\c!white] {} -- (y);
}
\draw (\f:\R) node [circle,scale=.3*\R,black!\c!white,fill=black!\c!white] {};
}
\end{tikzpicture}}
\foreach\n in {5,6,7,8,9,10,12,16,20} {
\eject
$$\nestedpolygon{\n}$$
}
\end{document}
See my follow-up post on the regular polygons arising in the hexagonal and triangular lattices. 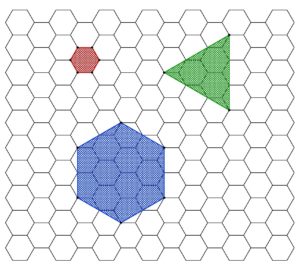


I really shouldn’t spoil the Book with technical detail, but the lattice is only invariant under /some/ rotations through pi/4. Also, that there would have to be a SMALLEST regular pentagon maybe requires an explanation, or at least a comment. Given two vectors in R^2, there is not always a shortest vector in the lattice they generate.
But you shouldn’t pay attention to such nitpicking.
The lattice is invariant under any
Yes, I am nitpicking. You write again: “if there is a regular pentagon in the square lattice, then there has to be one with smallest area”, a statement which requires proof. Contrast with the (false) statement: “if there is a convex pentagon in the square lattice, then there is one with smallest short diameter (the smallest distance between parallel lines that have the pentagon between them).” In your alternative version, while the areas clearly shrink, it is not clear that they shrink to zero.
As for lattices having short vectors, in more dimensions, given some vectors, finding the shortest vector in the lattice they generate is a hard problem (the LLL algorithm comes close in polynomial time), even when all of the generating vectors have integer coordinates.
While I’m nitpicking, let me add another complaint. You wrote “since the lattice is invariant under the reflection on any line through two of its lattice points”, which isn’t true. It is, however, invariant under the rotation that exchanges two of the points, which is just as good for these purposes.
But please don’t think I’m complaining! It’s a beautiful argument with extraordinary pictures, and thank you especially for including the code.
Thanks for the comments and corrections! I’ve edited to fix, using translations instead of reflections for the triangle case: two translations of the triangle along its sides give you all six vertices of the hexagon.
As for the point about smallest-instances, isn’t it obvious that for any fixed finite shape arising in the square lattice, there is a smallest instance? For a regular pentagon, say, for any given instance, there are only finitely many possible line segment lengths in the lattice that are smaller than the given side length, and so there will be a shortest possible side length that arises.
In your example case, the shapes are not all similar, so that isn’t the same type of thing. But for a fixed similarity type, I find the statement obvious. Alternatively, one could argue like this: what is the smallest square grid on which such a shape arises? The reduction argument shows that it can be made smaller. And the limit really is zero, since by similarity, the shrink factor is the same at each step.
re area, there is Pick’s Theorem, which is induced from how the area of a minimal lattice triangle is 1/2.
I’ve now got the result also for the hexagonal grid: the only regular (nondegenerate) polygons that occur are the triangle and the hexagon. I’ll make an updated post with new hexagonal images soon.
This reminds me of one of my favourite applications of the Pigeonhole principle.
> Theorem. Every (nondegenerate, not nec. regular) n-gon (n>4) with vertices on the integer lattice contains a lattice point in its interior.
Take an n-gon (n>4) with integer lattice points. Consider the vertex 4-colouring by (even, even), (even, odd), (odd,even) and (odd, odd).
By the pigeonhole principle, two of the n vertices must have the same colour. Therefore their midpoint is also an integer lattice point. (If it is in the interior, you’re done, otherwise the vertices are adjacent and you can shrink the n-gon.)
I’m a little late to the party, but I want to say this is an awesome post! I like your comment too, mpawliuk, but I’m not sure I understand the last step. If the two same-colored vertices are adjacent vertices, then how (and why) do you shrink the n-gon?
For instance, let’s say you have a pentagon and two of the vertices are at (0,0) and (0,2). What do you do to shrink it?
Pingback: There are no regular polygons in the hexagonal or triangular lattices, except triangles and hexagons | Joel David Hamkins
This post appeared in the Carnival of Mathematics 141!
I don’t understand where in your proof you show the length of the smller vector to be integers. Sure, you can build a saller pentagon this way, but the lengths won’t necessarily fall on the lattice vertices, thus there is no guaranteed smaller pentagon. For example, say the new length are 1/sqrt(2) of the old length: they would never fall on vertices of the lattice.
The new points were obtained by rotating lattice line segments about lattice points by ninety degrees, and the lattice is preserved by such an operation. Thus, the new points are indeed lattice points.
In order for anything to be embeddable on an integer lattice in any dimension,
it is necessary that all its distance ratios be square roots
of rational numbers. For a regular N-gon, if the side-length is 1,
then the distance between two vertices H hops apart along the polygon
is
sin(H*pi/N) * csc(pi/N)
by using the fact that circumradius=(1/2)*csc(pi/N).
So therefore, if for any two H values the ratio of the
(sin(H*pi/N) * csc(pi/N))^2
is irrational,
then no N-gon is embeddable on an integer lattice in any dimension.
When H=1 and 2 this formula simplifies and the criterion becomes
that
4*cos(pi/N)^2
be irrational. And this indeed is irrational for every N>0 besides 1,2,3,4,6.
J. H. Conway, C. Radin, L. Sadun:
On Angles Whose Squared Trigonometric Functions Are Rational,
Discrete & Computational Geometry 22 (1999) 321-332.
And sure enough, regular triangles and hexagons are embeddable in the 3D integer lattice
on planes x+y+z=constant, despite their non-embeddability in the plane,
and in the plane N=4 is embeddable, and on the line N=1 and 2.
So this completely settles the question for all N in all dimensions.
–Warren D. Smith
You seem to be saying that for n>6, n-gons can’t be made with vertices on integer lattice points in any dimension. But surely just taking the unit vectors in R^n will work? E.G. a heptagon in R^7 with vertices (1,0,0,0,0,0,0,0), (0,1,0,0,0,0,0), etc.
I assume this comment is addressed to me, rather than to Warren.
I would like to call your attention also to another argument, which works in any lattice (dimension doesn’t matter) and which appears in my book Proof and the Art of Mathematics (http://jdh.hamkins.org/proof-and-the-art-of-mathematics/), and which is also explained in this tweet: https://twitter.com/JDHamkins/status/1154865078493208576.
Meanwhile, your comment here is great! To be honest, it confused me terribly at first—what was going on? Then I realized, perhaps those points are not coplanar? Indeed, they are not. To see this, let’s subtract (1,0,0,0,0,0,0) from all your vectors, to put one vertex at the origin. The remaining points now include (-1,1,0,0,0,0,0), (-1,0,1,0,0,0,0), (-1,0,0,1,0,0,0) and so on. But these vectors do not span a two-dimensional space, since the first two are linearly independent, but no linear combination of them will produce the others. So your points do not form a regular heptagon, because they are not coplanar.
Pingback: What does this prove? Some of the most gorgeous visual "shrink" proofs ever invented | Dramaqu - Neoanime
Pingback: What does this prove? Some of the most gorgeous visual “shrink” proofs ever invented – Burkard Polster – Divagaciones en el Cinosargo