This will be a talk for the CUNY Logic Workshop on March 23, 2018, GC 6417 2-3:30pm.

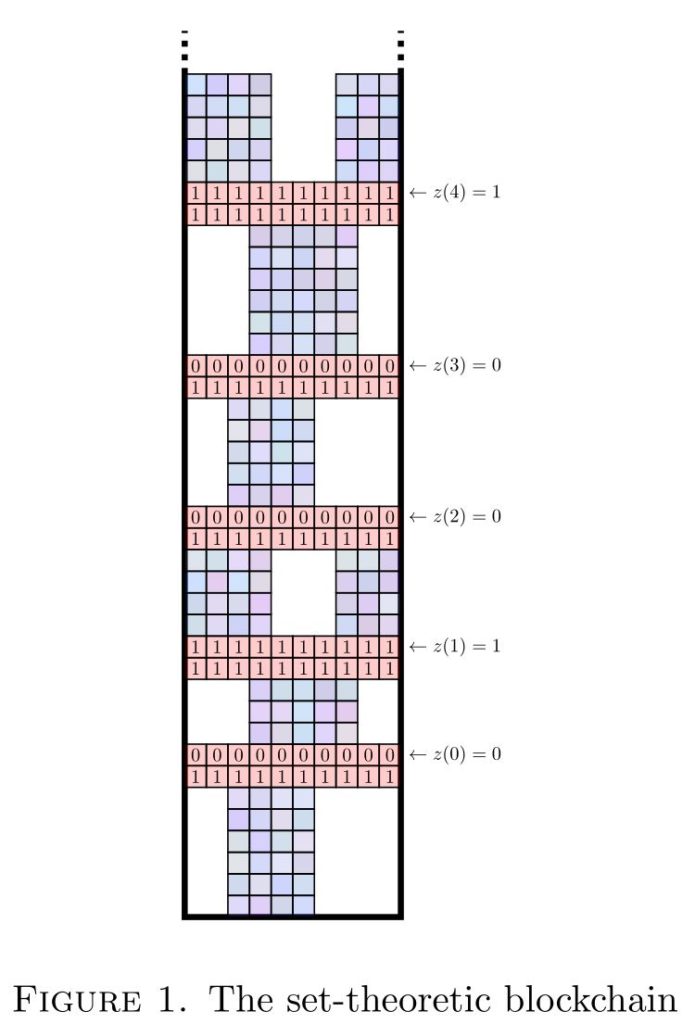
Abstract. Consider a countable model of set theory $M$ in the context of all its successive forcing extensions and grounds. This generic multiverse has long been known to exhibit instances of nonamalgamation: one can have two extensions $M[c]$ and $M[d]$, both adding a merely a generic Cohen real, which have no further extension in common. In this talk, I shall describe new joint work that illuminates the extent of non-amalgamation: every finite partial order (and more) embeds into the generic multiverse over any given model in a way that preserves amalgamability and non-amalgamability. The proof uses the set-theoretic blockchain argument (pictured above), which has affinities with constructions in computability theory in the Turing degrees. Other arguments, which also resemble counterparts in computability theory, show that the generic multiverse exhibits the exact pair phenonemon for increasing chains. This is joint work with Miha Habič, myself, Lukas Daniel Klausner and Jonathan Verner. The paper will be available this Spring.

• Upward countable closure in the generic multiverse of forcing to add a Cohen real
• Upward closure and amalgamation in the generic multiverse of a countable model of set theory
• Upward closure in the generic multiverse of a countable model of set theory, RIMS 2015, Kyoto, Japan
• Upward closure in the toy multiverse of all countable models of set theory

https://plus.google.com/u/0/+JoelDavidHamkins1/posts/NJp2N7bkkrR