I’d like to explain that one may find numerous nonstandard models of arithmetic as substructures of the field of complex numbers.
 The issue arose yesterday at Hans Schoutens’s talk for the CUNY Logic Workshop. The main focus of the talk was the question, for a given algebraically closed field of characteristic zero and a given model of arithmetic PA, whether and were jointly realizable as the set of powers (as he defines it) and the set of units of a model of the generalized theory of polynomial rings over fields. Very interesting stuff.
The issue arose yesterday at Hans Schoutens’s talk for the CUNY Logic Workshop. The main focus of the talk was the question, for a given algebraically closed field of characteristic zero and a given model of arithmetic PA, whether and were jointly realizable as the set of powers (as he defines it) and the set of units of a model of the generalized theory of polynomial rings over fields. Very interesting stuff.
During the talk, a side question arose, concerning exactly which models of PA arise as substructures of the field of complex numbers.
Question. Which models of PA arise as substructures of the field of complex numbers ?
Of course the standard model arises this way, and some people thought at first it should be difficult to realize nonstandard models of PA as substructures of . After some back and forth, the question was ultimately answered by Alfred Dolich in the pub after the seminar, and I’d like to give his argument here (but see the Mlček reference below). This is a case where a problem that was initially confusing becomes completely clear!
Theorem. Every model of PA of size at most continuum arises as a sub-semiring of the field of complex numbers .
Proof. Suppose that is a model of PA of size at most continuum. Inside , we may form ’s version of the algebraic numbers , the field that thinks is the algebraic closure of its version of the rationals. So is an algebraically closed field of characteristic zero, which has an elementary extension to such a field of size continuum. Since the theory of algebraically closed fields of characteristic zero is categorical in all uncountable powers, it follows that is isomorphic to a submodel of . Since itself is isomorphic to a substructure of its rationals , which sit inside , it follows that is isomorphic to a substructure of , as claimed. QED
In particular, every countable model of PA can be found as a substructure of the complex numbers.
Essentially the same argument shows the following.
Theorem. If is an uncountable algebraically closed field of characteristic zero, then every model of arithmetic PA of size at most the cardinality of embeds into .
I’ve realized that the same collection of ideas shows the following striking way to look upon the complex numbers:
Theorem. The complex numbers can be viewed as a nonstandard version of the algebraic numbers inside a nonstandard model of PA. Indeed, for every uncountable algebraically closed field of characteristic zero and every model of arithmetic PA of the same cardinality, the field is isomorphic to the nonstandard algebraic numbers as sees them.
Proof. Fix any such field , such as the complex numbers themselves, and consider any nonstandard model of arithmetic of the same cardinality. The field , which is ’s nonstandard version of the algebraic numbers, is an algebraically closed field of characteristic zero and same uncountable size as . By categoricity, these fields are isomorphic.
I had suspected that these results were folklore in the model-theoretic community, and it has come to my attention that proper credit for the main observation of this post seems to be due to Jozef Mlček, who proved it in 1973. Thanks to Jerome Tauber for the reference, which he provided in the comments.
 The issue arose yesterday at Hans Schoutens’s talk for the CUNY Logic Workshop. The main focus of the talk was the question, for a given algebraically closed field
The issue arose yesterday at Hans Schoutens’s talk for the CUNY Logic Workshop. The main focus of the talk was the question, for a given algebraically closed field 

Nice! Logicians and algebraists talk a bit differently so I’d like to check some things.
1) I’m pretty sure that “a submodel of C”, in this context, is just a subfield of C.
2) I’m getting confused about whether “A is an algebraically closed field of characteristic zero, which has an elementary extension to such a field of size continuum” means the same thing as “A is an algebraically closed field of characteristic zero, which has an extension to such a field of size continuum.” The latter is true, in any case.
I think one can avoid some scary logician words like “submodel”, “elementary extension” and “categorical” by saying this: “any algebraically closed field of characteristic zero whose cardinality is less than or equal to that of C is isomorphic to a subfield of C”. I’m forgetting if the proofs of this feel more like logic or like algebra.
All your comments are fine. Since the theory of algebraically closed fields of characteristic zero admits elimination of quantifiers, every subfield is an elementary submodel, and every field extension among such fields is an elementary extension.
To my way of thinking, one shouldn’t omit the word categorical, since it is precisely this fact that unifies so much of our knowledge in this case. The theory of algebraically closed fields of characteristic zero is categorical in every uncountable cardinality, which means that there is up to isomorphism precisely one such field of each uncountable cardinality. This explains why any field of characteristic zero and size at most continuum is isomorphic to a subfield of
Regarding your specific numbered comments, for (1), in general, a submodel means a substructure satisfying the same theory in question. In this case, it would mean not just a subfield, but an algebraically closed subfield. But in fact, one needs only subfield for the argument to work. For (2), those are equivalent precisely because of the quantifier elimination argument, and so amongst the algebraically closed fields, a field extension is the same as an elementary extension.
Thanks for all the clarifications! I agree that the uncountable categoricity of the theory of an algebraically closed field of characteristic zero is the engine that drives everything here. However, it’s a sad fact that lots of seemingly well-educated algebraists do not know the term “categorical” but will understand what one means by “two uncountable algebraically closed fields are isomorphic iff they have the same cardinality”. You’re running a logic blog so you shouldn’t resort to such baby-talk, but to reach a maximal audience I think one needs to… so that’s what I did on my blog. In math, alas, even popularizations require further popularization.
Thanks so much for your blog post; I appreciate it very much. I’m glad that my blog has such distinguished readers as yourself and your knowledgeable followers. It is amazing to me that someone’s observation in a pub after a seminar can subsequently reach such a huge number of interested parties.
Yes, despite the problems with quick electronic communication (which have been much in the news), it’s great how it speeds the spread of interesting mathematical and scientific knowledge. Your blog is great for feeding my hobbyist interest in mathematical logic, and when I hear something cool I want to tell everyone. And so it goes….
How much information does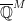 retain about the model
retain about the model  ? Could it be interesting to study nonstandard models of the natural numbers using these fields?
? Could it be interesting to study nonstandard models of the natural numbers using these fields?
The topic of Hans Schoutens talk was in part the idea of looking at
Neat!
Pingback: Nonstandard Integers as Complex Numbers | Azimuth
By the way, the usual definition of ‘characteristic zero’ for fields says that
So, if we have a nonstandard model of the natural numbers, we get a nonstandard notion of ‘characteristic zero’. Does that affect anything you’re talking about? You’re using facts about algebraically closed fields.
Can there be fields that have characteristic zero if we work with the standard model of PA but finite characteristic if we use a nonstandard model? (I’m not sure what this question even means, but I can’t resist asking it.)
Regarding my last question, I guess we can try where
where  is a nonstandard prime. This should have nonstandard characteristic.
is a nonstandard prime. This should have nonstandard characteristic.
What do people know about nonstandard primes? I guess in a nonstandard model there have to exist nonstandard primes, because none of the standard primes is ‘big enough’ to obtain a prime factorization for a nonstandard natural number.
It looks like we made the same observation at the same time! (see my next comment).
PA proves that there are infinitely many primes (since the usual proof can be undertaken in PA), or in other words, that they are unbounded, and so every nonstandard model of PA will definitely have lots of nonstandard primes. Indeed, there is always a prime between
You can consider a nonstandard version of
John and Joel,
It can also be interesting to study the Sylow p subgroups of a hyperfinite extension of a locally finite group, where p is an infinite hyperfinite prime hyperinteger. I looked at this a bit in my dissertation (1989, UH, “Nonstandard Methods and Finiteness Conditions in Algebra”). I never published the work I did on groups and rings in my dissertation. Instead, I took an interest in applying nonstandard methods to universal algebra, and lattices. Then I started my job here in Rolla Missouri, and I’ve had other collaborations since then, but I did extend some ring and field theoretic work from my M.S. thesis to topological models in a paper in Studia Logica. Back when I wrote my M.S. thesis, I had applied nonstandard methods to the Primitive Element Theorem from the theory of fields.
I’m curious what those results would inspire now in light of this result from the CUNY Logic Workshop…
Also in relation to this, if we fix a submodel A of the field of complex numbers that is a nonstandard model of PA, and let F be the subfield of C that is generated by A. It seems to me that F supports then a definable total order < that is compatible with its arithmetic (definable from the arithmetic in A?), and F is nonarchimedean relative to this order <, so that F includes infinitesimal elements. Is it clear what these infinitesimal elements look like, as elements of C?
Matt Insall
I really like your idea at the end about looking at the induced order on the field generated by the nonstandard model of PA. It seems to me that this field must be isomorphic to the rationals of the PA model, and the order will be definable from the arithmetic of the PA model.
As for what the infinitesimals “look like” as elements of
Commentationes Mathematicae Universitatis Carolinae
14,3 (1973)
A REPRESENTATION OP MODELS OP PEANO ARITHMETIC
J. MLCEK, Praha
Abstract: The following theorem is proved: algebraically Closed field of char. 0 is saturated if and only if every countable model of Peano arithmetic can be embedded into it.
Key words: Peano arithmetic, algebraically closed
field of char. 0 , saturated model, embedding.
AMS, Primary: 02H15 Ref. Z. 2.666
Introduction. In this paper, we shall present some results on embeddability of countable models of Peano arithmetic P into models of algebraically closed fields of characteristics 0 .
This set-theoretical result should be compared with(and was inspired by) a recent result of Vopenka saying that (under reasonable assumptions on existence of semisets) each countable model of P can be embedded into the field of real numbers by a semi-set embedding.
https://dml.cz/bitstream/handle/10338.dmlcz/105508/CommentatMathUnivCarol_014-1973-3_11.pdf
Thanks very much for this!
Harvey Friedman has kindly pointed out his 1992 JSL article with Robert K. Meyer, which contains some related material and results. I found that it is available via JStor at http://www.jstor.org/tc/accept?origin=/stable/pdf/2275433.pdf?refreqid=excelsior%3A7e994c8b2e5e010c6337380cea6e2860. He does not appear to cite the 1973 Mlček paper.
% From: Harvey Friedman, Joel David Hamkins
% Date: Sat, 3 Mar 2018 18:40:22 -0500
% Subject: Re: [New post] Nonstandard Integers as Complex Numbers
% To: baaz
%
% Have I been properly credited for my work in
%
% 43. (with R. K. Meyer), Wither Relevance Arithmetic?, Journal of Symbolic
% Logic, Vol. 57, No. 3, September 1992, pp. 824-831.
%
% ???
%
% see section 2, and footnote 6, my results going back to 1985.
%
% Harvey
%
% > John Baez posted: “I just read something cool: Joel David Hamkins,
% > Nonstandard models of arithmetic arise in the complex numbers, 3 March
% > 2018. Let me try to explain it in a simplified way. I think all cool math
% > should be known more widely than it is…
Very interesting post.
Just to ensure I’m not missing anything: you wrote “we construct A, the field that M thinks is the algebraic closure of its version of the rationals.” By “M thinks” you just mean that A is the model constructed as the fraction-field of elements of M, not that A is somehow internal to M, right?
No, I had meant the internal one. For the fraction-field, this will be the same as what you think is the fraction-field, but for the “algebraic closure” part, the internal construction will be adding roots of nonstandard-size polynomials, and so this will be different from what an algebraist would do externally when taking the algebraic closure.
But actually, you can use either one and still make a successful argument, since they will all embed into the desired field, and the model of arithmetic
Hi Joel, this is super interesting! I wonder, can we say anything about the (descriptive or otherwise) complexity of given model of
I ask because this seems relevant to the following open problem in models of PA: Recall that a Kaufmann model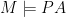 is an
is an 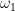 -like recursively saturated, rather classless model. Kaufmann constructed these using
-like recursively saturated, rather classless model. Kaufmann constructed these using 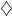 but then Shelah showed via a complicated absoluteness argument that such models exist in ZFC. The problem is to determine if one can actually build such a model without extra assumptions or whether the absoluteness is required in the proof. Since Kaufmann models are the right size, they embed into
but then Shelah showed via a complicated absoluteness argument that such models exist in ZFC. The problem is to determine if one can actually build such a model without extra assumptions or whether the absoluteness is required in the proof. Since Kaufmann models are the right size, they embed into 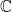 by this argument and I wonder if one can show that all such models, as subsets of
by this argument and I wonder if one can show that all such models, as subsets of 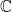 , must outstrip any kind of natural complexity this would suggest a negative solution to the problem.
, must outstrip any kind of natural complexity this would suggest a negative solution to the problem.
Hi Joel, the readers of your blog might be also interested in this related mathoverflow question(s) of mine, and the partial answers so far:
https://mathoverflow.net/questions/66146/nonstandard-reals-in-the-complex-plane
Thanks for the link, Ali. Very interesting questions!