[bibtex key=HamkinsYang:SatisfactionIsNotAbsolute]
Abstract. We prove that the satisfaction relation
of first-order logic is not absolute between models of set theory having the structure and the formulas all in common. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic , yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and the same arithmetic truths, yet disagree on their truths-about-truth, at any desired level of the iterated truth-predicate hierarchy; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have the same or the same rank-initial segment , yet disagree on which assertions are true in these structures. On the basis of these mathematical results, we argue that a philosophical commitment to the determinateness of the theory of truth for a structure cannot be seen as a consequence solely of the determinateness of the structure in which that truth resides. The determinate nature of arithmetic truth, for example, is not a consequence of the determinate nature of the arithmetic structure
itself, but rather, we argue, is an additional higher-order commitment requiring its own analysis and justification.
 Many mathematicians and philosophers regard the natural numbers
Many mathematicians and philosophers regard the natural numbers
Feferman provides an instance of this perspective when he writes (Feferman 2013, Comments for EFI Workshop, p. 6-7) :
In my view, the conception [of the bare structure of the natural numbers] is completely clear, and thence all arithmetical statements are definite.
It is Feferman’s `thence’ to which we call attention. Martin makes a similar point (Martin, 2012, Completeness or incompleteness of basic mathematical concepts):
What I am suggesting is that the real reason for confidence in first-order completeness is our confidence in the full determinateness of the concept of the natural numbers.
Many mathematicians and philosophers seem to share this perspective. The truth of an arithmetic statement, to be sure, does seem to depend entirely on the structure
 Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as
Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as
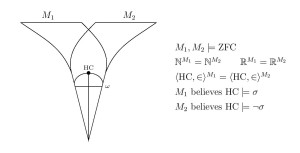
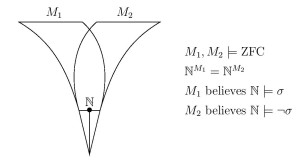
We make our argument in part by proving that different models of set theory can have a structure identically in common, even the natural numbers, yet disagree on the theory of truth for that structure.
Theorem.
- Two models of set theory can have the same structure of arithmetic
- Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is a well-order.
- Two models of set theory that have the same natural numbers and the same reals, yet disagree on projective truth.
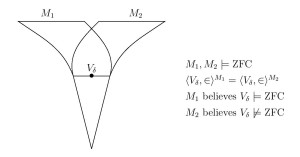
- Two models of set theory can have a transitive rank initial segment in common
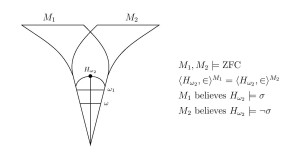 The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.
The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.


Pingback: Satisfaction is not absolute, Connecticut, October 2013 | Joel David Hamkins
Here I have some mathematical and philosophical questions:
1) In your non-absoluteness cases you give examples of two different models of ZFC which are agree on a certain structure but are not agree on what this model satisfies. For example they are agree on the notion of N but one of them believes that N is a model of a certain sentence P and another thinks that N is not a model of P. What is the source of this disagreement? Are these two models of ZFC agree on the notion of the statement P? Perhaps here the problem is not about the satisfaction relation and this difference in the point of views of these two models of ZFC is related to the different attitudes of the models M_1 and M_2 about the “meaning of the sentence P”. Because the definiteness of the satisfaction relation is dependent on definiteness of “both” first order “structures” and “sentences” in a certain mathematical world (model of ZFC).
Let me to add an example:
Consider Alice and Bob who are two archeologists with a same “ideology” (e.g. materialism). Both believes that “human” is just a configuration of atoms like any other object of the world and there is no spiritual being like a “soul” for a man. Some day Alice and Bob who are working on an ancient Egyptian grave find an ancient Papyrus. They cannot read it completely because they don’t know the meaning of some symbols but they can guess the meaning of the text from the readable words.
Alice: I guess the Papyrus says: “The sun gave soul to humans”.
Bob: No Alice. I think it says: “The sun gave life to humans”.
Now based on their materialistic ideology Alice thinks that the sentence on the Papyrus is false about humans but Bob believes that it is true about each human. This is a “misunderstanding” between them.
In this example Alice and Bob are two models of ZFC (ideology) agree on the notion of a certain structure (human) but disagree on the notion a given formal sentence (Text on the Papyrus) and so disagree on the truth value of this sentence on the model. Note that in this case based on their ideology Alice and Bob are agree on the “notion of satisfaction” in the models. Both of them believes that if the Papyrus says that humans have souls, it is a false sentence about the “human” as a model and otherwise it is true.
2) Are the facts which you introduced in this paper and also in your multiverse philosophy of mathematics refuting the “existence” of a “Platonistic world of the mathematical objects” or you are refuting its “uniqueness”?
It looks like a kind of “Pluralistic Platonism” which has a completely post-modern nature based on relativism and perhaps raised from living in a multinational society like NY as a paradigm.
3) Can we consider all of the different mathematical worlds as different “shadows” (or appearances) of a unique ideal world of mathematical objects? Note that these shadows can have contradictory properties if we consider them in an example like what I described in my MathOverflow question “Can we see invisible sets?”
Sorry for bothering (maybe)… An example (maybe) of a statement with two different meanings of the sentence in two different structures: L is a inner model of V, so it seems to have less sets than V. Howver, V+L implies that there exists unmeasurable subset in R, looks like that it makes subsets of R more, i.e. the sets become more. This seems to be a contradiction: after excluding some sets from V, L satisfies an existential proposition that cannot be satisfied by V. A simple and straightforward explanation: An existential propositional proposition \exists \phi (x) may be true in one model but false in another. But that does not make the former has “more elements” than the latter. It is because \phi (x) in \exists \phi (x) could be a complicated proposition, whose truth could be related to the “structure” of the model it is in.
or the simpler example: “countability” in different models of zfc.
I am not sure. Perhaps there is a problem on my browser. But the formulas appear in black color for me. It is a bit hard to read them in the (beauty) dark theme of the site.
Hmmnn. They look fine on my system. Is anyone else having trouble with them?
I installed a new version of my browser. It is fine now. Perhaps that was an incompatibility between softwares.
this indicates that your system forces MathJax to fall back to image fonts. if you’re using Firefox you might cause this by blocking web fonts. otherwise it’s a case of a bad connection and Mathjax timed out while downloading the web fonts.
Thanks for your useful advices Peter.
Isn’t the fact that satisfaction is not absolute a theorem of Jagger-Richards from 1965 published in “Out of Our Heads” US, vol. 2, no. 7? 🙂
Oh yes, their result has been released on the arxiv here:
An alternative (perhaps engineering-) version of the Jagger-Richards Theorem is as follows;
You can’t always get what you want, but it you try some time you just might find you get what you need.
This comes up in model-based digital image process algorithm research.
This is a very, very interesting paper. I did have a couple of question, though , regarding something you and Yang wrote on page 3:
So the slogan [Satisfaction is absolute!] is true to a very high degree, and in particular, it is true whenever the formula
Question 1: Could you give me an example of a circumstance in which
Question 2: When the term “access” is used in this sentence, is this ‘access’ the access relation found in modal semantics? If not, are these concept in any way related?
Also, in the case where every model of set theory (ZFC) has access to the satisfaction relation of every other model of set theory, would that imply that set theory is categorical? If not, why not?
What do you mean by categorical here? I think this is not the model theoretic notion of a categorical theory. is it?
Ali, it is. After all, what the paper shows is that if, say, two models of set theory agree on what the natural numbers are and have the same standard model of arithmetic (i.e.
Very useful explanation. Thank you very much.
Pingback: Satisfaction is not absolute, Dartmouth Logic Seminar, January 2014 | Joel David Hamkins
A note to Mitch: I would suggest starting your own blog, which might be a way for you to reach more people with your ideas. You can get started for free–check out wordpress.com.
Pingback: Does definiteness-of-truth follow from definiteness-of-objects? NY Philosophical Logic Group, NYU, November 2014 | Joel David Hamkins
Pingback: The absolute truth about non-absolute truth, JAF – Weak Arithmetic Days, New York, July 2015 | Joel David Hamkins
Pingback: Same structure, different truths, Stanford University CSLI, May 2016 | Joel David Hamkins
Pingback: Math Genius: Definition of structure and satisfaction on Set theory(ZFC). - TECHPRPR