[bibtex key=”HamkinsYao:Reflection-in-second-order-set-theory-with-abundant-urelements”]

Download pdf at arXiv:2204.09766

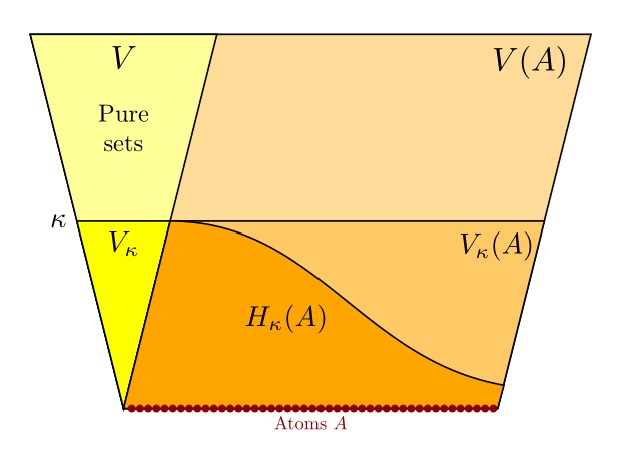
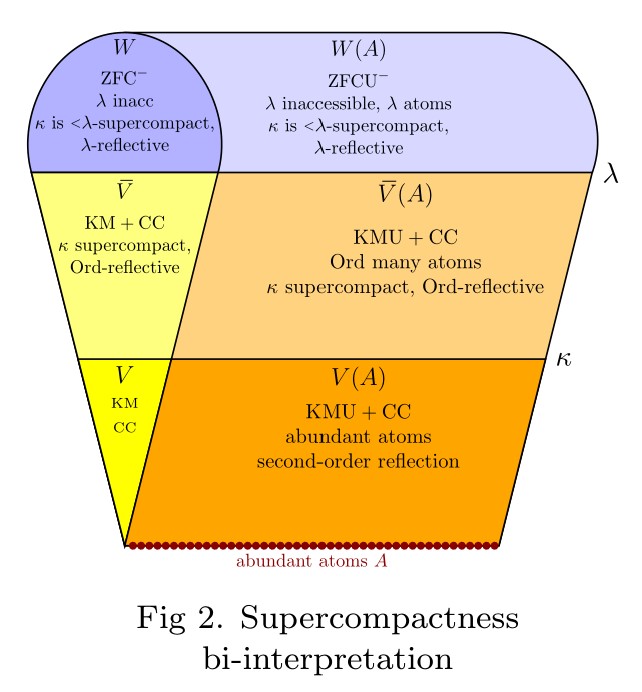
Abstract. After reviewing various natural bi-interpretations in urelement set theory, including second-order set theories with urelements, we explore the strength of second-order reflection in these contexts. Ultimately, we prove, second-order reflection with the abundant atom axiom is bi-interpretable and hence also equiconsistent with the existence of a supercompact cardinal. The proof relies on a reflection characterization of supercompactness, namely, a cardinal $\kappa$ is supercompact if and only if every ${\mathrm{\Pi }}_1^1$ sentence true in a structure $M$ (of any size) containing $\kappa$ in a language of size less than $\kappa$ is also true in a substructure $m\prec M$ of size less than $\kappa$ with $m\cap \kappa \in \kappa$.

See also my talk at the CUNY Set Theory Seminar: The surprising strength of reflection in second-order set theory with abundant urelements