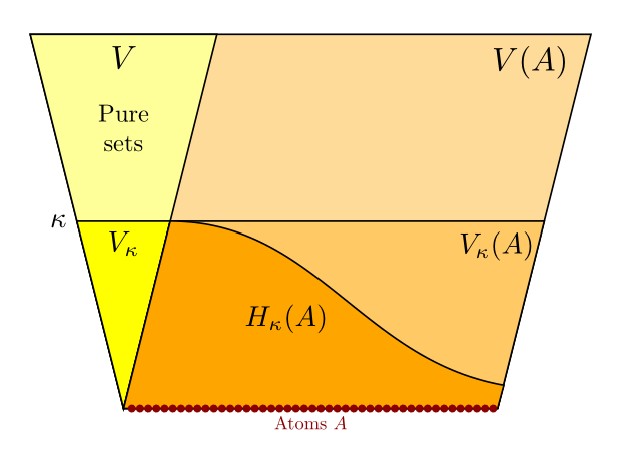
This will be a talk for the Set Theory in the UK, STUK 10, held in Oxford 14 June 2023, organized by my students Clara List, Emma Palmer, and Wojciech Wołoszyn.
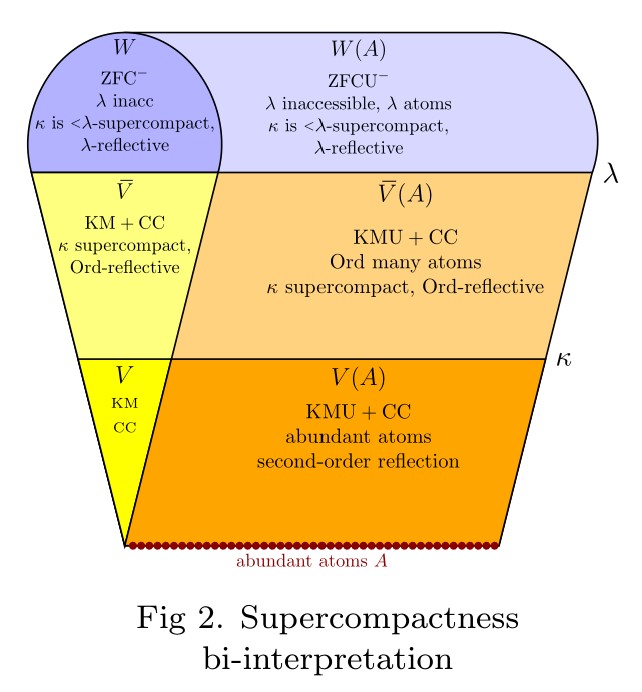
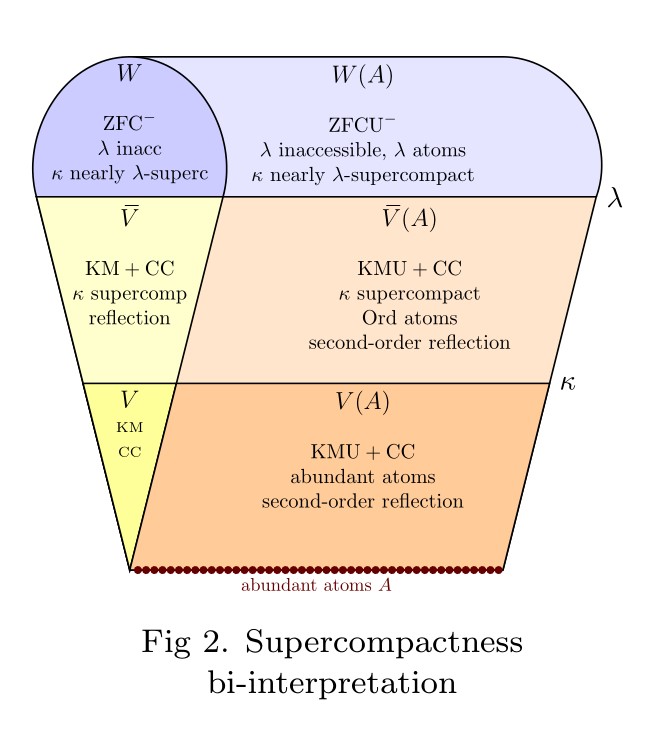
Abstract. I shall speak on the surprising strength of the second-order reflection principle in the context of set theory with abundant urelements. The theory GBcU with the abundant urelement axiom and second-order reflection is bi-interpretable with a strengthening of KM with a supercompact cardinal. This is joint work with Bokai Yao.
[bibtex key=”HamkinsYao:Reflection-in-second-order-set-theory-with-abundant-urelements”]
Download pdf at arXiv:2204.09766
Abstract. After reviewing various natural bi-interpretations in urelement set theory, including second-order set theories with urelements, we explore the strength of second-order reflection in these contexts. Ultimately, we prove, second-order reflection with the abundant atom axiom is bi-interpretable and hence also equiconsistent with the existence of a supercompact cardinal. The proof relies on a reflection characterization of supercompactness, namely, a cardinal $\kappa$ is supercompact if and only if every $\Pi^1_1$ sentence true in a structure $M$ (of any size) containing $\kappa$ in a language of size less than $\kappa$ is also true in a substructure $m\prec M$ of size less than $\kappa$ with $m\cap\kappa\in\kappa$.
See also my talk at the CUNY Set Theory Seminar: The surprising strength of reflection in second-order set theory with abundant urelements
This was an online talk 15 April 12:15 for the CUNY Set Theory Seminar. Held on Zoom at 876 9680 2366.
Abstract. I shall give a general introduction to urelement set theory and the role of the second-order reflection principle in second-order urelement set theory GBCU and KMU. With the abundant atom axiom, asserting that the class of urelements greatly exceeds the class of pure sets, the second-order reflection principle implies the existence of a supercompact cardinal in an interpreted model of ZFC. The proof uses a reflection characterization of supercompactness: a cardinal $\kappa$ is supercompact if and only if for every second-order sentence $\psi$ true in some structure $M$ (of any size) in a language of size less than $\kappa$ is also true in a first-order elementary substructure $m\prec M$ of size less than $\kappa$. This is joint work with Bokai Yao.
See the article at: Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal
This will be talk for the workshop Philosophy of Set Theory held at the University of Konstanz, 3 – 4 December 2021 — in person!
Update: Unfortunately, the workshop has been cancelled (perhaps postponed to next year) in light of the Covid resurgence.
Abstract. I shall analyze the roles and interaction of reflection and urelements in second-order set theory. Second-order reflection already exhibits large cardinal strength even without urelements, but recent work shows that in the presence of abundant urelements, second-order reflection is considerably stronger than might have been expected—at the level of supercompact cardinals. This is joint work with Bokai Yao (Notre Dame).
