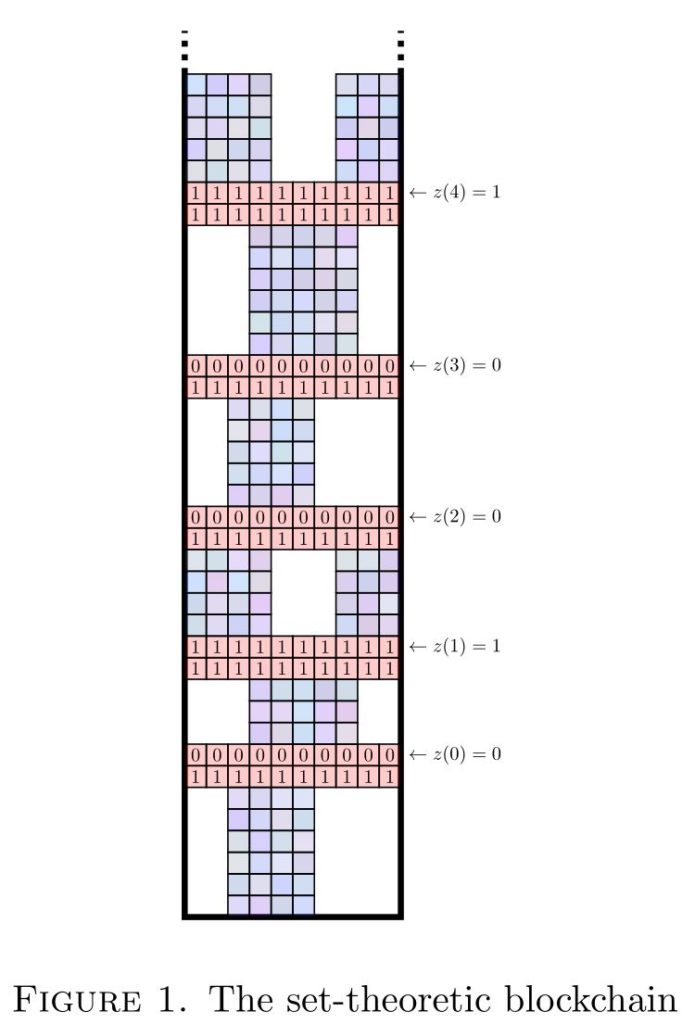
[bibtex key=”HabicHamkinsKlausnerVernerWilliams2018:Set-theoretic-blockchains”]
Abstract. Given a countable model of set theory, we study the structure of its generic multiverse, the collection of its forcing extensions and ground models, ordered by inclusion. Mostowski showed that any finite poset embeds into the generic multiverse while preserving the nonexistence of upper bounds. We obtain several improvements of his result, using what we call the blockchain construction to build generic objects with varying degrees of mutual genericity. The method accommodates certain infinite posets, and we can realize these embeddings via a wide variety of forcing notions, while providing control over lower bounds as well. We also give a generalization to class forcing in the context of second-order set theory, and exhibit some further structure in the generic multiverse, such as the existence of exact pairs.