Tag Archives: class forcing

Kelley-Morse set theory does not prove the class Fodor principle

Posted on by
Reply
    1. [bibtex key=”GitmanHamkinsKaragila:KM-set-theory-does-not-prove-the-class-Fodor-theorem”]

Abstract.
We show that Kelley-Morse (KM) set theory does not prove the class Fodor principle, the assertion that every regressive class function $F:S\to\newcommand\Ord{\text{Ord}}\Ord$ defined on a stationary class $S$ is constant on a stationary subclass. Indeed, it is relatively consistent with KM for any infinite $\lambda$ with $\omega\leq\lambda\leq\Ord$ that there is a class function $F:\Ord\to\lambda$ that is not constant on any stationary class. Strikingly, it is consistent with KM that there is a class $A\subseteq\omega\times\Ord$, such that each section $A_n=\{\alpha\mid (n,\alpha)\in A\}$ contains a class club, but $\bigcap_n A_n$ is empty. Consequently, it is relatively consistent with KM that the class club filter is not $\sigma$-closed.

The class Fodor principle is the assertion that every regressive class function $F:S\to\Ord$ defined on a stationary class $S$ is constant on a stationary subclass of $S$. This statement can be expressed in the usual second-order language of set theory, and the principle can therefore be sensibly considered in the context of any of the various second-order set-theoretic systems, such as Gödel-Bernays (GBC) set theory or Kelley-Morse (KM) set theory. Just as with the classical Fodor’s lemma in first-order set theory, the class Fodor principle is equivalent, over a weak base theory, to the assertion that the class club filter is normal. We shall investigate the strength of the class Fodor principle and try to find its place within the natural hierarchy of second-order set theories. We shall also define and study weaker versions of the class Fodor principle.

If one tries to prove the class Fodor principle by adapting one of the classical proofs of the first-order Fodor’s lemma, then one inevitably finds oneself needing to appeal to a certain second-order class-choice principle, which goes beyond the axiom of choice and the global choice principle, but which is not available in Kelley-Morse set theory. For example, in one standard proof, we would want for a given $\Ord$-indexed sequence of non-stationary classes to be able to choose for each member of it a class club that it misses. This would be an instance of class-choice, since we seek to choose classes here, rather than sets. The class choice principle $\text{CC}(\Pi^0_1)$, it turns out, is sufficient for us to make these choices, for this principle states that if every ordinal $\alpha$ admits a class $A$ witnessing a $\Pi^0_1$-assertion $\varphi(\alpha,A)$, allowing class parameters, then there is a single class $B\subseteq \Ord\times V$, whose slices $B_\alpha$ witness $\varphi(\alpha,B_\alpha)$; and the property of being a class club avoiding a given class is $\Pi^0_1$ expressible.

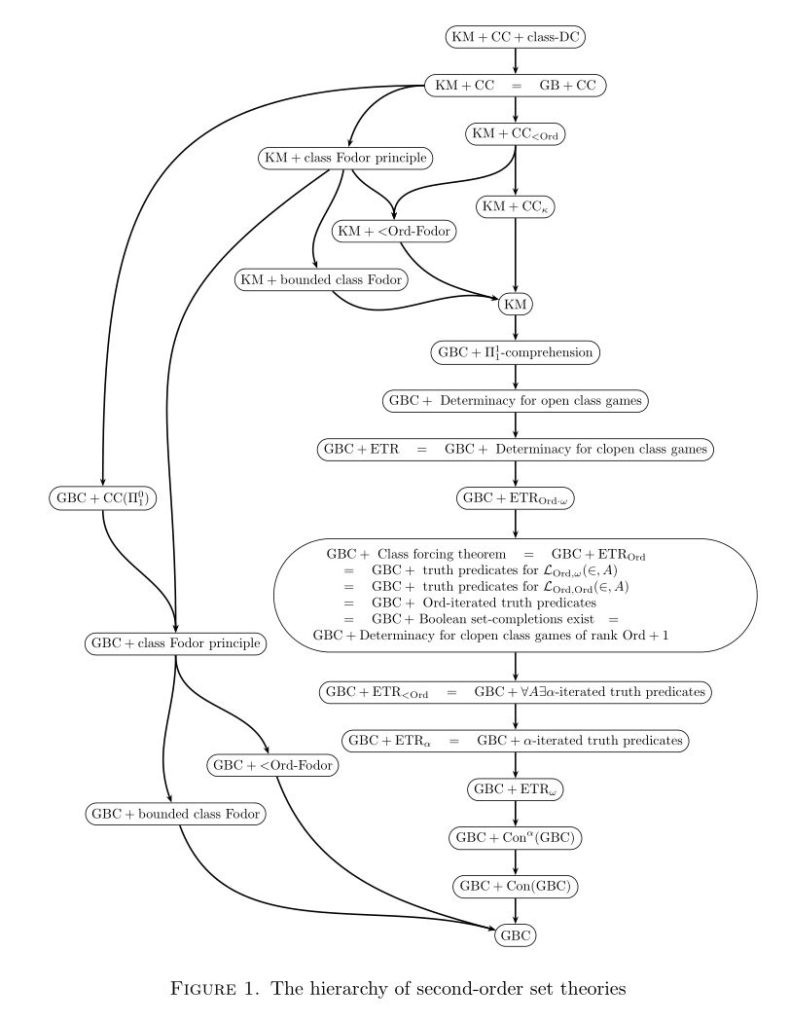
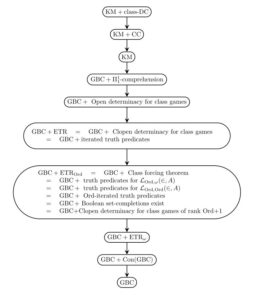
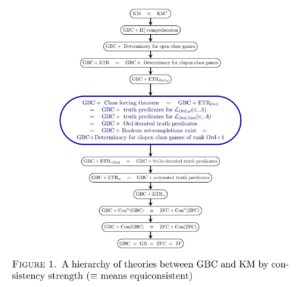
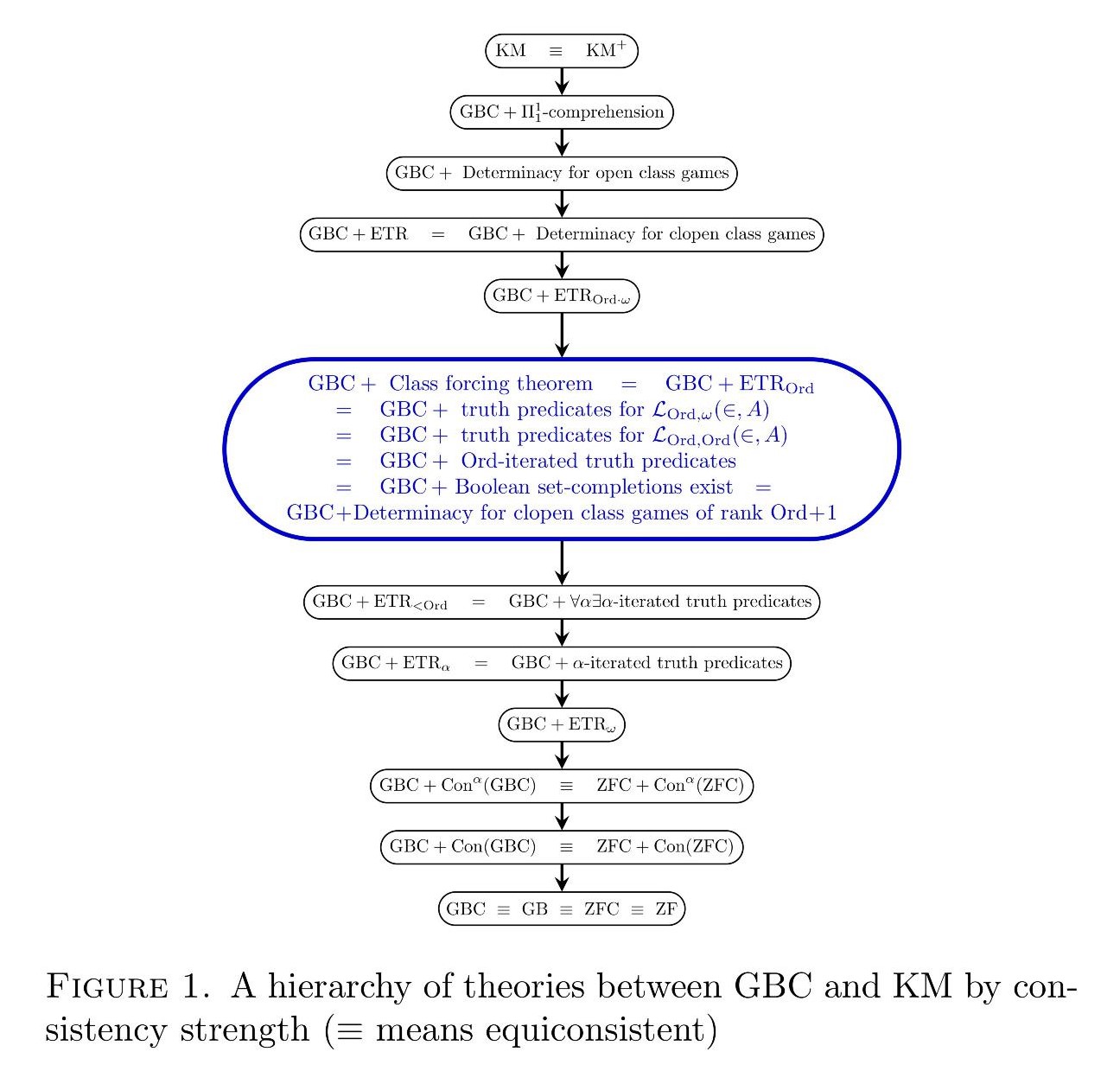
Thus, the class Fodor principle, and consequently also the normality of the class club filter, is provable in the relatively weak second-order set theory $\text{GBC}+\text{CC}(\Pi^0_1)$. This theory is known to be weaker in consistency strength than the theory $\text{GBC}+\Pi^1_1$-comprehension, which is itself strictly weaker in consistency strength than KM.

But meanwhile, although the class choice principle is weak in consistency strength, it is not actually provable in KM; indeed, even the weak fragment $\text{CC}(\Pi^0_1)$ is not provable in KM. Those results were proved several years ago by the first two authors, but they can now be seen as consequences of the main result of this article (see corollary 15. In light of that result, however, one should perhaps not have expected to be able to prove the class Fodor principle in KM.

Indeed, it follows similarly from arguments of the third author in his dissertation that if $\kappa$ is an inaccessible cardinal, then there is a forcing extension $V[G]$ with a symmetric submodel $M$ such that $V_\kappa^M=V_\kappa$, which implies that $\mathcal M=(V_\kappa,\in, V^M_{\kappa+1})$ is a model of Kelley-Morse, and in $\mathcal M$, the class Fodor principle fails in a very strong sense.

In this article, adapting the ideas of Karagila to the second-order set-theoretic context and using similar methods as in Gitman and Hamkins’s previous work on KM, we shall prove that every model of KM has an extension in which the class Fodor principle fails in that strong sense: there can be a class function $F:\Ord\to\omega$, which is not constant on any stationary class. In particular, in these models, the class club filter is not $\sigma$-closed: there is a class $B\subseteq\omega\times\Ord$, each of whose vertical slices $B_n$ contains a class club, but $\bigcap B_n$ is empty.

Main Theorem. Kelley-Morse set theory KM, if consistent, does not prove the class Fodor principle. Indeed, if there is a model of KM, then there is a model of KM with a class function $F:\Ord\to \omega$, which is not constant on any stationary class; in this model, therefore, the class club filter is not $\sigma$-closed.

We shall also investigate various weak versions of the class Fodor principle.

Definition.

  1. For a cardinal $\kappa$, the class $\kappa$-Fodor principle asserts that every class function $F:S\to\kappa$ defined on a stationary class $S\subseteq\Ord$ is constant on a stationary subclass of $S$.
  2. The class ${<}\Ord$-Fodor principle is the assertion that the $\kappa$-class Fodor principle holds for every cardinal $\kappa$.
  3. The bounded class Fodor principle asserts that every regressive class function $F:S\to\Ord$ on a stationary class $S\subseteq\Ord$ is bounded on a stationary subclass of $S$.
  4. The very weak class Fodor principle asserts that every regressive class function $F:S\to\Ord$ on a stationary class $S\subseteq\Ord$ is constant on an unbounded subclass of $S$.

We shall separate these principles as follows.

Theorem. Suppose KM is consistent.

  1. There is a model of KM in which the class Fodor principle fails, but the class ${<}\Ord$-Fodor principle holds.
  2. There is a model of KM in which the class $\omega$-Fodor principle fails, but the bounded class Fodor principle holds.
  3. There is a model of KM in which the class $\omega$-Fodor principle holds, but the bounded class Fodor principle fails.
  4. $\text{GB}^-$ proves the very weak class Fodor principle.

Finally, we show that the class Fodor principle can neither be created nor destroyed by set forcing.

Theorem. The class Fodor principle is invariant by set forcing over models of $\text{GBC}^-$. That is, it holds in an extension if and only if it holds in the ground model.

Let us conclude this brief introduction by mentioning the following easy negative instance of the class Fodor principle for certain GBC models. This argument seems to be a part of set-theoretic folklore. Namely, consider an $\omega$-standard model of GBC set theory $M$ having no $V_\kappa^M$ that is a model of ZFC. A minimal transitive model of ZFC, for example, has this property. Inside $M$, let $F(\kappa)$ be the least $n$ such that $V_\kappa^M$ fails to satisfy $\Sigma_n$-collection. This is a definable class function $F:\Ord^M\to\omega$ in $M$, but it cannot be constant on any stationary class in $M$, because by the reflection theorem there is a class club of cardinals $\kappa$ such that $V_\kappa^M$ satisfies $\Sigma_n$-collection.

Read more by going to the full article: [bibtex key=”GitmanHamkinsKaragila:KM-set-theory-does-not-prove-the-class-Fodor-theorem”]

 

 

Set-theoretic blockchains

Posted on by
1

[bibtex key=”HabicHamkinsKlausnerVernerWilliams2018:Set-theoretic-blockchains”]

Abstract. Given a countable model of set theory, we study the structure of its generic multiverse, the collection of its forcing extensions and ground models, ordered by inclusion. Mostowski showed that any finite poset embeds into the generic multiverse while preserving the nonexistence of upper bounds. We obtain several improvements of his result, using what we call the blockchain construction to build generic objects with varying degrees of mutual genericity. The method accommodates certain infinite posets, and we can realize these embeddings via a wide variety of forcing notions, while providing control over lower bounds as well. We also give a generalization to class forcing in the context of second-order set theory, and exhibit some further structure in the generic multiverse, such as the existence of exact pairs.

Open class determinacy is preserved by forcing

Posted on by
Reply

[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]

Abstract. The principle of open class determinacy is preserved by pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Similarly, the principle of elementary transfinite recursion ETR${}_\Gamma$ for a fixed class well-order $\Gamma$ is preserved by pre-tame class forcing. The full principle ETR itself is preserved by countably strategically closed pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Meanwhile, it remains open whether ETR is preserved by all forcing, including the forcing merely to add a Cohen real.

 

The principle of elementary transfinite recursion ETR — according to which every first-order class recursion along any well-founded class relation has a solution — has emerged as a central organizing concept in the hierarchy of second-order set theories from Gödel-Bernays set theory GBC up to Kelley-Morse set theory KM and beyond. Many of the principles in the hierarchy can be seen as asserting that certain class recursions have solutions.

In addition, many of these principles, including ETR and its variants, are equivalently characterized as determinacy principles for certain kinds of class games. Thus, the hierarchy is also fruitfully unified and organized by determinacy ideas.

This hierarchy of theories is the main focus of study in the reverse mathematics of second-order set theory, an emerging subject aiming to discover the precise axiomatic principles required for various arguments and results in second-order set theory. The principle ETR itself, for example, is equivalent over GBC to the principle of clopen determinacy for class games and also to the existence of iterated elementary truth predicates (see Open determinacy for class games); since every clopen game is also an open game, the principle ETR is naturally strengthened by the principle of open determinacy for class games, and this is a strictly stronger principle (see Hachtman and Sato); the weaker principle ETR${}_\text{Ord}$, meanwhile, asserting solutions to class recursions of length Ord, is equivalent to the class forcing theorem, which asserts that every class forcing notion admits a forcing relation, to the existence of set-complete Boolean completions of any class partial order, to the existence of Ord-iterated elementary truth predicates, to the determinacy of clopen games of rank at most Ord+1, and to other natural set-theoretic principles (see The exact strength of the class forcing theorem).

Since one naturally seeks in any subject to understand how one’s fundamental principles and tools interact, we should like in this article to consider how these second-order set-theoretic principles are affected by forcing. These questions originated in previous work of Victoria Gitman and myself, and question 1 also appears in the dissertation of Kameryn Williams, which was focused on the structure of models of second-order set theories.

It is well-known, of course, that ZFC, GBC, and KM are preserved by set forcing and by tame class forcing, and this is true for other theories in the hierarchy, such as GBC$+\Pi^1_n$-comprehension and higher levels of the second-order comprehension axiom. The corresponding forcing preservation theorem for ETR and for open class determinacy, however, has not been known.

Question 1. Is ETR preserved by forcing?

Question 2. Is open class determinacy preserved by forcing?

We intend to ask in each case about class forcing as well as set forcing. Question 1 is closely connected with the question of whether forcing can create new class well-order order types, longer than any class well-order in the ground model. Specifically, Victoria Gitman and I had observed earlier that ETR${}_\Gamma$ for a specific class well-order $\Gamma$ is preserved by pre-tame class forcing, and this would imply that the full principle ETR would also be preserved, if no fundamentally new class well-orders are created by the forcing. In light of the fact that forcing over models of ZFC adds no new ordinals, that would seem reasonable, but proof is elusive, and the question remains open. Can forcing add new class well-orders, perhaps very tall ones that are not isomorphic to any ground model class well-order? Perhaps there are some very strange models of GBC that gain new class well-order order types in a forcing extension.

Question 3. Assume GBC. After forcing, must every new class well-order be isomorphic to a ground-model class well-order? Does ETR imply this?

The main theorem of this article provides a full affirmative answer to question 2, and partial affirmative answers to questions 2 and 3.

Main Theorem.

  1. Open class determinacy is preserved by pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.
  2. The principle ETR${}_\Gamma$, for any fixed class well order $\Gamma$, is preserved by pre-tame class forcing.
  3. The full principle ETR is preserved by countably strategically closed pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.

We should like specifically to highlight the fact that questions 1 and 3 remain open even in the case of the forcing to add a Cohen real. Is ETR preserved by the forcing to add a Cohen real? After adding a Cohen real, is every new class well-order isomorphic to a ground-model class well-order? One naturally expects affirmative answers, especially in a model of ETR.

For more, click through the arxiv for a pdf of the full article.

[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]

The set-theoretic universe is not necessarily a class-forcing extension of HOD

Posted on by
Reply

[bibtex key=”HamkinsReitz:The-set-theoretic-universe-is-not-necessarily-a-forcing-extension-of-HOD”]

Abstract. In light of the celebrated theorem of Vopěnka, proving in ZFC that every set is generic over $\newcommand\HOD{\text{HOD}}\HOD$, it is natural to inquire whether the set-theoretic universe $V$ must be a class-forcing extension of $\HOD$ by some possibly proper-class forcing notion in $\HOD$. We show, negatively, that if ZFC is consistent, then there is a model of ZFC that is not a class-forcing extension of its $\HOD$ for any class forcing notion definable in $\HOD$ and with definable forcing relations there (allowing parameters). Meanwhile, S. Friedman (2012) showed, positively, that if one augments $\HOD$ with a certain ZFC-amenable class $A$, definable in $V$, then the set-theoretic universe $V$ is a class-forcing extension of the expanded structure $\langle\HOD,\in,A\rangle$. Our result shows that this augmentation process can be necessary. The same example shows that $V$ is not necessarily a class-forcing extension of the mantle, and the method provides a counterexample to the intermediate model property, namely, a class-forcing extension $V\subseteq V[G]$ by a certain definable tame forcing and a transitive intermediate inner model $V\subseteq W\subseteq V[G]$ with $W\models\text{ZFC}$, such that $W$ is not a class-forcing extension of $V$ by any class forcing notion with definable forcing relations in $V$. This improves upon a previous example of Friedman (1999) by omitting the need for $0^\sharp$.

 

In 1972, Vopěnka proved the following celebrated result.

Theorem. (Vopěnka) If $V=L[A]$ where $A$ is a set of ordinals, then $V$ is a forcing extension of the inner model $\HOD$.

The result is now standard, appearing in Jech (Set Theory 2003, p. 249) and elsewhere, and the usual proof establishes a stronger result, stated in ZFC simply as the assertion: every set is generic over $\HOD$. In other words, for every set $a$ there is a forcing notion $\mathbb{B}\in\HOD$ and a $\HOD$-generic filter $G\subseteq\mathbb{B}$ for which $a\in\HOD[G]\subseteq V$. The full set-theoretic universe $V$ is therefore the union of all these various set-forcing generic extensions $\HOD[G]$.

It is natural to wonder whether these various forcing extensions $\HOD[G]$ can be unified or amalgamated to realize $V$ as a single class-forcing extension of $\HOD$ by a possibly proper class forcing notion in $\HOD$. We expect that it must be a very high proportion of set theorists and set-theory graduate students, who upon first learning of Vopěnka’s theorem, immediately ask this question.

Main Question. Must the set-theoretic universe $V$ be a class-forcing extension of $\HOD$?

We intend the question to be asking more specifically whether the universe $V$ arises as a bona-fide class-forcing extension of $\HOD$, in the sense that there is a class forcing notion $\mathbb{P}$, possibly a proper class, which is definable in $\HOD$ and which has definable forcing relation $p\Vdash\varphi(\tau)$ there for any desired first-order formula $\varphi$, such that $V$ arises as a forcing extension $V=\HOD[G]$ for some $\HOD$-generic filter $G\subseteq\mathbb{P}$, not necessarily definable.

In this article, we shall answer the question negatively, by providing a model of ZFC that cannot be realized as such a class-forcing extension of its $\HOD$.

Main Theorem. If ZFC is consistent, then there is a model of ZFC which is not a forcing extension of its $\HOD$ by any class forcing notion definable in that $\HOD$ and having a definable forcing relation there.

Throughout this article, when we say that a class is definable, we mean that it is definable in the first-order language of set theory allowing set parameters.

The main theorem should be placed in contrast to the following result of Sy Friedman.

Theorem. (Friedman 2012) There is a definable class $A$, which is strongly amenable to $\HOD$, such that the set-theoretic universe $V$ is a generic extension of $\langle \HOD,\in,A\rangle$.

This is a postive answer to the main question, if one is willing to augment $\HOD$ with a class $A$ that may not be definable in $\HOD$. Our main theorem shows that in general, this kind of augmentation process is necessary.

It is natural to ask a variant of the main question in the context of set-theoretic geology.

Question. Must the set-theoretic universe $V$ be a class-forcing extension of its mantle?

The mantle is the intersection of all set-forcing grounds, and so the universe is close in a sense to the mantle, perhaps one might hope that it is close enough to be realized as a class-forcing extension of it. Nevertheless, the answer is negative.

Theorem. If ZFC is consistent, then there is a model of ZFC that does not arise as a class-forcing extension of its mantle $M$ by any class forcing notion with definable forcing relations in $M$.

We also use our results to provide some counterexamples to the intermediate-model property for forcing. In the case of set forcing, it is well known that every transitive model $W$ of ZFC set theory that is intermediate $V\subseteq W\subseteq V[G]$ a ground model $V$ and a forcing extension $V[G]$, arises itself as a forcing extension $W=V[G_0]$.

In the case of class forcing, however, this can fail.

Theorem. If ZFC is consistent, then there are models of ZFC set theory $V\subseteq W\subseteq V[G]$, where $V[G]$ is a class-forcing extension of $V$ and $W$ is a transitive inner model of $V[G]$, but $W$ is not a forcing extension of $V$ by any class forcing notion with definable forcing relations in $V$.

Theorem. If ZFC + Ord is Mahlo is consistent, then one can form such a counterexample to the class-forcing intermediate model property $V\subseteq W\subseteq V[G]$, where $G\subset\mathbb{B}$ is $V$-generic for an Ord-c.c. tame definable complete class Boolean algebra $\mathbb{B}$, but nevertheless $W$ does not arise by class forcing over $V$ by any definable forcing notion with a definable forcing relation.

More complete details, please go to the paper (click through to the arxiv for a pdf). [bibtex key=”HamkinsReitz:The-set-theoretic-universe-is-not-necessarily-a-forcing-extension-of-HOD”]

The hierarchy of second-order set theories between GBC and KM and beyond

Posted on by
3

This was a talk at the upcoming International Workshop in Set Theory at the Centre International de Rencontres Mathématiques at the Luminy campus in Marseille, France, October 9-13, 2017.

Hierarchy between GBC and KM

Abstract. Recent work has clarified how various natural second-order set-theoretic principles, such as those concerned with class forcing or with proper class games, fit into a new robust hierarchy of second-order set theories between Gödel-Bernays GBC set theory and Kelley-Morse KM set theory and beyond. For example, the principle of clopen determinacy for proper class games is exactly equivalent to the principle of elementary transfinite recursion ETR, strictly between GBC and GBC+$\Pi^1_1$-comprehension; open determinacy for class games, in contrast, is strictly stronger; meanwhile, the class forcing theorem, asserting that every class forcing notion admits corresponding forcing relations, is strictly weaker, and is exactly equivalent to the fragment $\text{ETR}_{\text{Ord}}$ and to numerous other natural principles. What is emerging is a higher set-theoretic analogue of the familiar reverse mathematics of second-order number theory.

Slides

https://plus.google.com/u/0/+JoelDavidHamkins1/posts/ekgdakenadv

The exact strength of the class forcing theorem

Posted on by
2

[bibtex key=”GitmanHamkinsHolySchlichtWilliams2020:The-exact-strength-of-the-class-forcing-theorem”]

Abstract. The class forcing theorem, which asserts that every class forcing notion $\newcommand\P{\mathbb{P}}\P$ admits a forcing relation $\newcommand\forces{\Vdash}\forces_\P$, that is, a relation satisfying the forcing relation recursion — it follows that statements true in the corresponding forcing extensions are forced and forced statements are true — is equivalent over Gödel-Bernays set theory GBC to the principle of elementary transfinite recursion $\newcommand\Ord{\text{Ord}}\newcommand\ETR{\text{ETR}}\ETR_{\Ord}$ for class recursions of length $\Ord$. It is also equivalent to the existence of truth predicates for the infinitary languages $\mathcal{L}_{\Ord,\omega}(\in,A)$, allowing any class parameter $A$; to the existence of truth predicates for the language $\mathcal{L}_{\Ord,\Ord}(\in,A)$; to the existence of $\Ord$-iterated truth predicates for first-order set theory $\mathcal{L}_{\omega,\omega}(\in,A)$; to the assertion that every separative class partial order $\P$ has a set-complete class Boolean completion; to a class-join separation principle; and to the principle of determinacy for clopen class games of rank at most $\Ord+1$. Unlike set forcing, if every class forcing relation $\P$ has a forcing relation merely for atomic formulas, then every such $\P$ has a uniform forcing relation that applies uniformly to all formulas. Our results situate the class forcing theorem in the rich hierarchy of theories between GBC and Kelley-Morse set theory KM.

We shall characterize the exact strength of the class forcing theorem, which asserts that every class forcing notion $\P$ has a corresponding forcing relation $\forces_\P$, a relation satisfying the forcing relation recursion. When there is such a forcing relation, then statements true in any corresponding forcing extension are forced and forced statements are true in those extensions.

Unlike the case of set forcing, where one may prove in ZFC that every set forcing notion has corresponding forcing relations, for class forcing it is consistent with Gödel-Bernays set theory GBC that there is a proper class forcing notion lacking a corresponding forcing relation, even merely for the atomic formulas. For certain forcing notions, the existence of an atomic forcing relation implies Con(ZFC) and much more, and so the consistency strength of the class forcing theorem strictly exceeds GBC, if this theory is consistent. Nevertheless, the class forcing theorem is provable in stronger theories, such as Kelley-Morse set theory. What is the exact strength of the class forcing theorem?

Our project here is to identify the strength of the class forcing theorem by situating it in the rich hierarchy of theories between GBC and KM, displayed in part in the figure above, with the class forcing theorem highlighted in blue. It turns out that the class forcing theorem is equivalent over GBC to an attractive collection of several other natural set-theoretic assertions; it is a robust axiomatic principle.

Hierarchy between GBC and KM

The main theorem is naturally part of the emerging subject we call the reverse mathematics of second-order set theory, a higher analogue of the perhaps more familiar reverse mathematics of second-order arithmetic. In this new research area, we are concerned with the hierarchy of second-order set theories between GBC and KM and beyond, analyzing the strength of various assertions in second-order set theory, such as the principle ETR of elementary transfinite recursion, the principle of $\Pi^1_1$-comprehension or the principle of determinacy for clopen class games. We fit these set-theoretic principles into the hierarchy of theories over the base theory GBC. The main theorem of this article does exactly this with the class forcing theorem by finding its exact strength in relation to nearby theories in this hierarchy.

Main Theorem. The following are equivalent over Gödel-Bernays set theory.

  1. The atomic class forcing theorem: every class forcing notion admits forcing relations for atomic formulas $$p\forces\sigma=\tau\qquad\qquad p\forces\sigma\in\tau.$$
  2. The class forcing theorem scheme: for each first-order formula $\varphi$ in the forcing language, with finitely many class names $\dot \Gamma_i$, there is a forcing relation applicable to this formula and its subformulas
    $$p\forces\varphi(\vec \tau,\dot\Gamma_0,\ldots,\dot\Gamma_m).$$
  3. The uniform first-order class forcing theorem: every class forcing notion $\P$ admits a uniform forcing relation $$p\forces\varphi(\vec \tau),$$ applicable to all assertions $\varphi$ in the first-order forcing language with finitely many class names $\mathcal{L}_{\omega,\omega}(\in,V^\P,\dot\Gamma_0,\ldots,\dot\Gamma_m)$.
  4. The uniform infinitary class forcing theorem: every class forcing notion $\P$ admits a uniform forcing relation $$p\forces\varphi(\vec \tau),$$ applicable to all assertions $\varphi$ in the infinitary forcing language with finitely many class names $\mathcal{L}_{\Ord,\Ord}(\in,V^\P,\dot\Gamma_0,\ldots,\dot\Gamma_m)$.
  5. Names for truth predicates: every class forcing notion $\P$ has a class name $\newcommand\T{{\rm T}}\dot\T$ and a forcing relation for which $1\forces\dot\T$ is a truth-predicate for the first-order forcing language with finitely many class names $\mathcal{L}_{\omega,\omega}(\in,V^\P,\dot\Gamma_0,\ldots,\dot\Gamma_m)$.
  6. Every class forcing notion $\P$, that is, every separative class partial order, admits a Boolean completion $\mathbb{B}$, a set-complete class Boolean algebra into which $\P$ densely embeds.
  7. The class-join separation principle plus $\ETR_{\Ord}$-foundation.
  8. For every class $A$, there is a truth predicate for $\mathcal{L}_{\Ord,\omega}(\in,A)$.
  9. For every class $A$, there is a truth predicate for $\mathcal{L}_{\Ord,\Ord}(\in,A)$.
  10. For every class $A$, there is an $\Ord$-iterated truth predicate for $\mathcal{L}_{\omega,\omega}(\in,A)$.
  11. The principle of determinacy for clopen class games of rank at most $\Ord+1$.
  12. The principle $\ETR_{\Ord}$ of elementary transfinite recursion for $\Ord$-length recursions of first-order properties, using any class parameter.

Implication cycle 12

We prove the theorem by establishing the complete cycle of indicated implications. The red arrows indicate more difficult or substantive implications, while the blue arrows indicate easier or nearly immediate implications. The green dashed implication from statement (12) to statement (1), while not needed for the completeness of the implication cycle, is nevertheless used in the proof that (12) implies (4). The proof of (12) implies (7) also uses (8), which follows from the fact that (12) implies (9) implies (8).

For more, download the paper from the arxiv: [bibtex key=”GitmanHamkinsHolySchlichtWilliams:The-exact-strength-of-the-class-forcing-theorem”]

See also Victoria’s post, Kameryn’s post.

The definable cut of a model of set theory can be changed by small forcing

Posted on by
2

Cupid carving his bow -- ParmigianinoIf $M$ is a model of ZFC set theory, let $I$ be the definable cut of its ordinals, the collection of ordinals that are below an ordinal $\delta$ of $M$ that is definable in $M$ without parameters. This would include all the ordinals of $M$, if the definable ordinals happen to be unbounded in $M$, but one can also construct examples where the definable cut is bounded in $M$.  Let $M_I$ be the corresponding definable cut of $M$ itself, the rank-initial segment of $M$ determined by $I$, or in other words, the collection of all sets $x$ in $M$ of rank below a definable ordinal of $M$. Equivalently, $$M_I=\bigcup_{\delta\in I} V_\delta^M.$$ It is not difficult to see that this is an elementary substructure $M_I\prec M$, because we can verify the Tarski-Vaught criterion as follows. If $M\models\exists y\ \varphi(x,y)$, where $x\in M_I$, then let $\delta$ be a definable ordinal above the rank of $x$. In this case, the ordinal $\theta$, which is the supremum over all $a\in V_\delta$ of the minimal rank of a set $y$ for which $\varphi(a,y)$, if there is such a $y$. This supremum $\theta$ is definable, and so since $x\in V_\delta$, the minimal rank of a $y$ such that $\varphi(x,y)$ is at most $\theta$. Consequently, since $\theta\in I$, such a $y$ can be found in $M_I$. So we have found the desired witness inside the substructure, and so it is elementary $M_I\prec M$. Note that in the general case, one does not necessarily know that $I$ has a least upper bound in $M$. Under suitable assumptions, it can happen that $I$ is unbounded in $M$, that $I$ is an ordinal of $M$, or that $I$ is bounded in $M$, but has no least upper bound.

What I am interested in for this post is how the definable cut might be affected by forcing. Of course, it is easy to see that if $M$ is definable in $M[G]$, then the definable cut of $M[G]$ is at least as high as the definable cut of $M$, simply because the definable ordinals of $M$ remain definable in $M[G]$.

A second easy observation is that if the definable cut of $M$ is bounded in $M$, then we could perform large collapse forcing, collapsing a cardinal above $I$ to $\omega$, which would of course make every cardinal of $I$ countable in the extension $M[G]$. In this case, since $\omega_1^{M[G]}$ is definable, it would change the definable cut. So this kind of very large forcing can change the definable cut, making it larger.

But what about small forcing? Suppose that the forcing notion $\newcommand\P{\mathbb{P}}\P$ we intend to forcing with is small in the sense that it is in the definable cut $M_I$. This would be true if $\P$ itself were definable, for example, but really we only require that $\P$ has rank less than some definable ordinal of $M$. Can this forcing change the definable cut?

Let me show at least that the definable cut can never go up after small forcing.

Theorem. If $G\subset\P$ is $M$-generic for forcing $\P$ in the definable cut of $M$, then the definable cut of $M[G]$ is below or the same in the ordinals as it was in $M$.

Proof. Suppose that $G\subset\P$ is $M$-generic, and we consider the forcing extension $M[G]$. We have already proved that $M_I\prec M$ is an elementary submodel. I claim that this relation lifts to the forcing extension $M_I[G]\prec M[G]$. Note first that since $\P\in M_I$ and $M_I$ is a rank initial segment of $M$, it follows that $M_I$ has all the subsets of $\P$ in $M$, and so $G$ is $M_I$-generic. So the extension $M_I[G]$ makes sense. Next, suppose that $M[G]\models\varphi(a)$ for some $a\in M_I[G]$. If $\dot a$ is a name for $a$ in $M_I$, then there is some condition $p\in G$ forcing $\varphi(\dot a)$ over $M$. Since $M_I\prec M$, this is also forced by $p$ over $M_I$, and thus $M_I[G]\models\varphi(a)$ as well, as desired. So $M_I[G]\prec M[G]$, and from this it follows that every definable ordinal of $M[G]$ is in the cut $I$. So the definable cut did not get higher. QED

But can it go down? Not if the model $M$ is definable in $M[G]$, by our earlier easy observation. Consequently,

Theorem. If $M$ is definable in $M[G]$, where $G\subset\P$ is $M$-generic for forcing $\P$ below the definable cut of $M$, then the definable cut of $M[G]$ is the same as the definable cut of $M$.

Proof. It didn’t go down, since $M$ is definable in $M[G]$; and it didn’t go up, since $\P$ was small. QED

What if $M$ is not definable in $M[G]$? Can we make the definable cut go down after small forcing? The answer is yes.

Theorem. If ZFC is consistent, then there is a model $M\models\text{ZFC}$ with a definable notion of forcing $\P$ (hence in the definable cut of $M$), such that if $G\subset\P$ is $M$-generic, then the definable cut of the forcing extension $M[G]$ is strictly shorter than the definable cut of $M[G]$.

Proof. Start with a model of $\text{ZFC}+V=L$, whose definable ordinals are bounded by a cardinal $\delta$. Let’s call it $L$, and let $I$ be the definable cut of $L$, which we assume is bounded by $\delta$. Let $M=L[G]$ be the forcing extension of $L$ obtained by performing an Easton product, adding a Cohen subset to every regular cardinal above $\delta$ in $L$. Since this forcing adds no sets below $\delta$, but adds a Cohen set at $\delta^+$, it follows that $\delta$ becomes definable in $L[G]$. In fact, since the forcing is homogeneous and definable from $\delta$, it follows that the definable ordinals of $L[G]$ are precisely the ordinals that are definable in $L$ with parameter $\delta$. These may be bounded or unbounded in $L[G]$. Now, let $\newcommand\Q{\mathbb{Q}}\Q$ be the Easton product forcing at the stages below $\delta$, and suppose that $G\subset\Q$ is $L[G]$-generic. Consider the model $L[G][H]$. Note that the forcing $\Q$ is definable in $L[G]$, since $\delta$ is definable there. This two-step forcing can be combined into one giant Easton product in $L$, the product that simply forces to add a Cohen subset to every regular cardinal. Since this version of the forcing is homogeneous and definable in $L$, it follows that the definable ordinals of $L[G][H]$ are precisely the definable ordinals of $L$, which are bounded by $I$. In summary, the definable cut of $L[G]$ is strictly above $\delta$, since $\delta$ is definable in $L[G]$, and the forcing $\Q$ has size and rank $\delta$; but the forcing extension $L[G][H]$ has definable cut $I$, which is strictly bounded by $\delta$. So the definable cut was made smaller by small forcing, as claimed. QED

This post is an account of some ideas that Alexander Block and I had noted today during the course of our mathematical investigation of another matter.

Regula Krapf, Ph.D. 2017, University of Bonn

Posted on by
4

Regula Krapf successfully defended her PhD dissertation January 12, 2017 at the University of Bonn, with a dissertation entitled, “Class forcing and second-order arithmetic.”  I was a member of the dissertation examining committee. Peter Koepke was the dissertation supervisor.

Regula Krapf

Regula Krapf, Class forcing and second-order arithmetic, dissertation 2017, University of Bonn. (Slides)

Abstract. We provide a framework in a generalization of Gödel-Bernays set theory for performing class forcing. The forcing theorem states that the forcing relation is a (definable) class in the ground model (definability lemma) and that every statement that holds in a class-generic extension is forced by a condition in the generic filter (truth lemma). We prove both positive and negative results concerning the forcing theorem. On the one hand, we show that the definability lemma for one atomic formula implies the forcing theorem for all formulae in the language of set theory to hold. Furthermore, we introduce several properties which entail the forcing theorem. On the other hand, we give both counterexamples to the definability lemma and the truth lemma. In set forcing, the forcing theorem can be proved for all forcing notions by constructing a unique Boolean completion. We show that in class forcing the existence of a Boolean completion is essentially equivalent to the forcing theorem and, moreover, Boolean completions need not be unique.

The notion of pretameness was introduced to characterize those forcing notions which preserve the axiom scheme of replacement. We present several new characterizations of pretameness in terms of the forcing theorem, the preservation of separation, the existence of nice names for sets of ordinals and several other properties. Moreover, for each of the aforementioned properties we provide a corresponding characterization of the Ord-chain condition.

Finally, we prove two equiconsistency results which compare models of ZFC (with large cardinal properties) and models of second-order arithmetic with topological regularity properties (and determinacy hypotheses). We apply our previous results on class forcing to show that many important arboreal forcing notions preserve the $\Pi^1_1$-perfect set property over models of second-order arithmetic and also give an example of a forcing notion which implies the $\Pi^1_1$-perfect set property to fail in the generic extension.

Regula has now taken up a faculty position at the University of Koblenz.