Category Archives: Publications

The rearrangement number

Posted on by
3

[bibtex key=BlassBrendleBrianHamkinsHardyLarson2020:TheRearrangementNumber]

Abstract.  How many permutations of the natural numbers are needed so that every conditionally convergent series of real numbers can be rearranged to no longer converge to the same sum? We show that the minimum number of permutations needed for this purpose, which we call the rearrangement number, is uncountable, but whether it equals the cardinal of the continuum is independent of the usual axioms of
set theory. We compare the rearrangement number with several natural variants, for example one obtained by requiring the rearranged series to still converge but to a new, finite limit. We also compare the rearrangement number with several well-studied
cardinal characteristics of the continuum. We present some new forcing constructions designed to add permutations that rearrange series from the ground model in particular ways, thereby obtaining consistency results going beyond those that follow from comparisons with familiar cardinal characteristics. Finally we deal briefly with some variants concerning rearrangements by a special sort of permutations and with rearranging some divergent series to become (conditionally) convergent.

This project started with Michael Hardy’s question on MathOverflow, How many rearrangements must fail to alter the value of a sum before you conclude that none do? I had proposed in my answer that we should think of the cardinal in question as a cardinal characteristic of the continuum, the rearrangement number, since we could prove that it was uncountable and that it was the continuum under MA, and had begun to separate it from other familiar cardinal characteristics. Eventually, the research effort grew into the collaboration of this paper. What a lot of fun!

Colloquium talk at Vassar | Lecture notes | talk at CUNY | the original MathOverflow question

The lecture notes are for an introductory talk on the topic I had given at the Vassar College Mathematics Colloquium.

Ord is not definably weakly compact

Posted on by
2

[bibtex key=EnayatHamkins2018:Ord-is-not-definably-weakly-compact]

In ZFC the class of all ordinals is very like a large cardinal.  Being closed under exponentiation, for example, Ord is a strong limit.  Indeed, it is a beth fixed point. And Ord is regular with respect to definable classes by the replacement axiom.  In this sense, ZFC therefore proves that Ord is definably inaccessible.  Which other large cardinal properties are exhibited by Ord? Perhaps you wouldn’t find it unreasonable for Ord to exhibit, at least consistently with ZFC, the definable proper class analogues of other much stronger large cardinal properties?

Meanwhile, the main results of this paper, joint between myself and Ali Enayat, show that such an expectation would be misplaced, even for comparatively small large cardinal properties. Specifically, in a result that surprised me, it turns out that the class of ordinals NEVER exhibits the definable proper class analogue of weak compactness in any model of ZFC.

Theorem. The class of ordinals is not definably weakly compact. In every model of ZFC:

  1. The definable tree property fails; there is a definable Ord-tree with no definable cofinal branch.
  2. The definable partition property fails; there is a definable 2-coloring of a definable proper class, with no homogeneous definable proper subclass.
  3. The definable compactness property fails for $\mathcal{L}_{\mathrm{Ord,\omega}}$; there is a definable theory in this logic, all of whose set-sized subtheories are satisfiable, but the whole theory has no definable class model.

The proof uses methods from the model theory of set theory, including especially the fact that no model of ZFC has a conservative $\Sigma_3$-elementary end-extension.

Theorem. The definable $\Diamond _{\mathrm{Ord}}$ principle holds in a model of ZFC if and only if the model has a definable well-ordering.

We close the paper by proving that the theory of the spartan models of Gödel-Bernays set theory GB — those equipped with only their definable classes — is $\Pi^1_1$-complete.

Theorem. The set of sentences true in all spartan models of GB is $\Pi_{1}^{1}$-complete.

The Vopěnka principle is inequivalent to but conservative over the Vopěnka scheme

Posted on by
6

[bibtex key=Hamkins:The-Vopenka-principle-is-inequivalent-to-but-conservative-over-the-Vopenka-scheme]

Abstract. The Vopěnka principle, which asserts that every proper class of first-order structures in a common language admits an elementary embedding between two of its members, is not equivalent over GBC to the first-order Vopěnka scheme, which makes the Vopěnka assertion only for the first-order definable classes of structures. Nevertheless, the two Vopěnka axioms are equiconsistent and they have exactly the same first-order consequences in the language of set theory. Specifically, GBC plus the Vopěnka principle is conservative over ZFC plus the Vopěnka scheme for first-order assertions in the language of set theory.

Indras Net-03

The Vopěnka principle is the assertion that for every proper class $\mathcal{M}$ of first-order $\mathcal{L}$-structures, for a set-sized language $\mathcal{L}$, there are distinct members of the class $M,N\in\mathcal{M}$ with an elementary embedding $j:M\to N$ between them. In quantifying over classes, this principle is a single assertion in the language of second-order set theory, and it makes sense to consider the Vopěnka principle in the context of a second-order set theory, such as Godel-Bernays set theory GBC, whose language allows one to quantify over classes. In this article, GBC includes the global axiom of choice.

In contrast, the first-order Vopěnka scheme makes the Vopěnka assertion only for the first-order definable classes $\mathcal{M}$ (allowing parameters). This theory can be expressed as a scheme of first-order statements, one for each possible definition of a class, and it makes sense to consider the Vopěnka scheme in Zermelo-Frankael ZFC set theory with the axiom of choice.

Because the Vopěnka principle is a second-order assertion, it does not make sense to refer to it in the context of ZFC set theory, whose first-order language does not allow quantification over classes; one typically retreats to the Vopěnka scheme in that context. The theme of this article is to investigate the precise meta-mathematical interactions between these two treatments of Vopěnka’s idea.

Main Theorems.

  1. If ZFC and the Vopěnka scheme holds, then there is a class forcing extension, adding classes but no sets, in which GBC and the Vopěnka scheme holds, but the Vopěnka principle fails.
  2. If ZFC and the Vopěnka scheme holds, then there is a class forcing extension, adding classes but no sets, in which GBC and the Vopěnka principle holds.

It follows that the Vopěnka principle VP and the Vopěnka scheme VS are not equivalent, but they are equiconsistent and indeed, they have the same first-order consequences.

Corollaries.

  1. Over GBC, the Vopěnka principle and the Vopěnka scheme, if consistent, are not equivalent.
  2. Nevertheless, the two Vopěnka axioms are equiconsistent over GBC.
  3. Indeed, the two Vopěnka axioms have exactly the same first-order consequences in the language of set theory. Specifically, GBC plus the Vopěnka principle is conservative over ZFC plus the Vopěnka scheme for assertions in the first-order language of set theory. $$\text{GBC}+\text{VP}\vdash\phi\qquad\text{if and only if}\qquad\text{ZFC}+\text{VS}\vdash\phi$$

These results grew out of my my answer to a MathOverflow question of Mike Shulman, Can Vopěnka’s principle be violated definably?, inquiring whether there would always be a definable counterexample to the Vopěnka principle, whenever it should happen to fail. I interpret the question as asking whether the Vopěnka scheme is necessarily equivalent to the Vopěnka principle, and the answer is negative.

The proof of the main theorem involves the concept of a stretchable set $g\subset\kappa$ for an $A$-extendible cardinal, which has the property that for every cardinal $\lambda>\kappa$ and every extension $h\subset\lambda$ with $h\cap\kappa=g$, there is an elementary embedding $j:\langle V_\lambda,\in,A\cap V_\lambda\rangle\to\langle V_\theta,\in,A\cap V_\theta\rangle$ such that $j(g)\cap\lambda=h$. Thus, the set $g$ can be stretched by an $A$-extendibility embedding so as to agree with any given $h$.

Set-theoretic mereology

Posted on by
11

[bibtex key=HamkinsKikuchi2016:Set-theoreticMereology]

Abstract. We consider a set-theoretic version of mereology based on the inclusion relation $\newcommand\of{\subseteq}\of$ and analyze how well it might serve as a foundation of mathematics. After establishing the non-definability of $\in$ from $\of$, we identify the natural axioms for $\of$-based mereology, which constitute a finitely axiomatizable, complete, decidable theory. Ultimately, for these reasons, we conclude that this form of set-theoretic mereology cannot by itself serve as a foundation of mathematics. Meanwhile, augmented forms of set-theoretic mereology, such as that obtained by adding the singleton operator, are foundationally robust.

In light of the comparative success of membership-based set theory in the foundations of mathematics, since the time of Cantor, Zermelo and Hilbert, a mathematical philosopher naturally wonders whether one might find a similar success for mereology, based upon a mathematical or set-theoretic parthood relation rather than the element-of relation $\in$. Can set-theoretic mereology serve as a foundation of mathematics? And what should be the central axioms of set-theoretic mereology?

Venn_Diagram_of_sets_((P),(Q),(R))We should like therefore to consider a mereological perspective in set theory, analyzing how well it might serve as a foundation while identifying the central axioms. Although set theory and mereology, of course, are often seen as being in conflict, what we take as the project here is to develop and investigate, within set theory, a set-theoretic interpretation of mereological ideas. Mereology, by placing its focus on the parthood relation, seems naturally interpreted in set theory by means of the inclusion relation $\of$, so that one set $x$ is a part of another $y$, just in case $x$ is a subset of $y$, written $x\of y$. This interpretation agrees with David Lewis’s Parts of Classes (1991) interpretation of set-theoretic mereology in the context of sets and classes, but we restrict our attention to the universe of sets. So in this article we shall consider the formulation of set-theoretic mereology as the study of the structure $\langle V,\of\rangle$, which we shall take as the canonical fundamental structure of set-theoretic mereology, where $V$ is the universe of all sets; this is in contrast to the structure $\langle V,{\in}\rangle$, usually taken as central in set theory. The questions are: How well does this mereological structure serve as a foundation of mathematics? Can we faithfully interpret the rest of mathematics as taking place in $\langle V,\of\rangle$ to the same extent that set theorists have argued (with whatever degree of success) that one may find faithful representations in $\langle V,{\in}\rangle$? Can we get by with merely the subset relation $\of$ in place of the membership relation $\in$?

Ultimately, we shall identify grounds supporting generally negative answers to these questions. On the basis of various mathematical results, our main philosophical thesis will be that the particular understanding of set-theoretic mereology via the inclusion relation $\of$ cannot adequately serve by itself as a foundation of mathematics. Specifically, the following theorem and corollary show that $\in$ is not definable from $\of$, and we take this to show that one may not interpret membership-based set theory itself within set-theoretic mereology in any straightforward, direct manner.

Theorem. In any universe of set theory $\langle V,{\in}\rangle$, there is a definable relation $\in^*$, different from $\in$, such that $\langle V,{\in^*}\rangle$ is a model of set theory, in fact isomorphic to the original universe $\langle V,{\in}\rangle$, for which the corresponding inclusion relation $$u\subseteq^* v\quad\longleftrightarrow\quad \forall a\, (a\in^* u\to a\in^* v)$$ is identical to the usual inclusion relation $u\subseteq v$.

Corollary. One cannot define $\in$ from $\subseteq$ in any model of set theory, even allowing parameters in the definition.

A counterpoint to this is provided by the following theorem, however, which identifies a weak sense in which $\of$ may identify $\in$ up to definable automorphism of the universe.

Theorem. Assume ZFC in the universe $\langle V,\in\rangle$. Suppose that $\in^*$ is a definable class relation in $\langle V,{\in}\rangle$ for which $\langle V,\in^*\rangle$ is a model of set theory (a weak set theory suffices), such that the corresponding inclusion relation $$u\subseteq^* v\quad\iff\quad\forall a\,(a\in^* u\to a\in^* v)$$is the same as the usual inclusion relation $u\subseteq v$. Then the two membership relations are isomorphic $$\langle V,\in\rangle\cong\langle V,\in^*\rangle.$$

That counterpoint is not decisive, however, in light of the question whether we really need $\in^*$ to be a class with respect to $\in$, a question resolved by the following theorem, which shows that set-theoretic mereology does not actually determine the $\in$-isomorphism class or even the $\in$-theory of the $\in$-model in which it arises.

Theorem. For any two consistent theories extending ZFC, there are models $\langle W,{\in}\rangle$ and $\langle W,{\in^*}\rangle$ of those theories, respectively, with the same underlying set $W$ and the same induced inclusion relation $\of=\of^*$.

For example, we cannot determine in $\of$-based set-theoretic mereology whether the continuum hypothesis holds or fails, whether the axiom of choice holds or fails or whether there are large cardinals or not. Initially, the following central theorem may appear to be a positive result for mereology, since it identifies precisely what are the principles of set-theoretic mereology, considered as the theory of $\langle V,{\of}\rangle$. Namely, $\of$ is an atomic unbounded relatively complemented distributive lattice, and this is a finitely axiomatizable complete theory. So in a sense, this theory simply is the theory of $\of$-based set-theoretic mereology.

Theorem. Set-theoretic mereology, considered as the theory of $\langle V,\of\rangle$, is precisely the theory of an atomic unbounded relatively complemented distributive lattice, and furthermore, this theory is finitely axiomatizable, complete and decidable.

But upon reflection, since every finitely axiomatizable complete theory is decidable, the result actually appears to be devastating for set-theoretic mereology as a foundation of mathematics, because a decidable theory is much too simple to serve as a foundational theory for all mathematics. The full spectrum and complexity of mathematics naturally includes all the instances of many undecidable decision problems and so cannot be founded upon a decidable theory. Finally, it follows as a corollary that the structure consisting of the hereditarily finite sets under inclusion forms an elementary substructure of the full set-theoretic mereological universe $$\langle \text{HF},\of\rangle\prec\langle V,\of\rangle.$$ Consequently set-theoretic mereology cannot properly treat or even express the various concepts of infinity that arise in mathematics.

Mereology on MathOverflow | Mereology on Stanford Encyclopedia of Philosophy | Mereology on Wikipedia

Some previous posts on this blog:

Different models of set theory with same $\of$ | $\of$ is decidable

Upward closure and amalgamation in the generic multiverse of a countable model of set theory

Posted on by
7

[bibtex key=Hamkins2016:UpwardClosureAndAmalgamationInTheGenericMultiverse]

Abstract. I prove several theorems concerning upward closure and amalgamation in the generic multiverse of a countable transitive model of set theory. Every such model $W$ has forcing extensions $W[c]$ and $W[d]$ by adding a Cohen real, which cannot be amalgamated in any further extension, but some nontrivial forcing notions have all their extensions amalgamable. An increasing chain $W[G_0]\subseteq W[G_1]\subseteq\cdots$ has an upper bound $W[H]$ if and only if the forcing had uniformly bounded essential size in $W$. Every chain $W\subseteq W[c_0]\subseteq W[c_1]\subseteq \cdots$ of extensions adding Cohen reals is bounded above by $W[d]$ for some $W$-generic Cohen real $d$.

This article is based upon I talk I gave at the conference on Recent Developments in Axiomatic Set Theory at the Research Institute for Mathematical Sciences (RIMS) at Kyoto University, Japan in September, 2015, and I am extremely grateful to my Japanese hosts, especially Toshimichi Usuba, for supporting my research visit there and also at the CTFM conference at Tokyo Institute of Technology just preceding it. This article includes material adapted from section section 2 of Set-theoretic geology, joint with G. Fuchs, myself and J. Reitz, and also includes a theorem that was proved in a series of conversations I had with Giorgio Venturi at the Young Set Theory Workshop 2011 in Bonn and continuing at the London 2011 summer school on set theory at Birkbeck University London.

A position in infinite chess with game value $\omega^4$

Posted on by
17

[bibtex key=EvansHamkinsPerlmutter2017:APositionInInfiniteChessWithGameValueOmega^4]

Abstract.  We present a position in infinite chess exhibiting an ordinal game value of $\omega^4$, thereby improving on the previously largest-known values of $\omega^3$ and $\omega^3\cdot 4$.

This is a joint work with Cory Evans and Norman Perlmutter, continuing the research program of my previous article with Evans, Transfinite game values in infinite chess, namely, the research program of finding positions in infinite chess with large transfinite ordinal game values. In the previous article, Cory and I presented a position with game value $\omega^3$. In the current paper, with Norman Perlmutter now having joined us accompanied by some outstanding ideas, we present a new position having game value $\omega^4$, breaking the previous record.

Full position value omega^4

A position in infinite chess with value $\omega^4$

In the new position, above, the kings sit facing each other in the throne room, an uneasy détente, while white makes steady progress in the rook towers. Meanwhile, at every step black, doomed, mounts increasingly desperate bouts of long forced play using the bishop cannon battery, with bishops flying with force out of the cannons, and then each making a long series of forced-reply moves in the terminal gateways. Ultimately, white wins with value omega^4, which exceeds the previously largest known values of omega^3.

In the throne room, if either black or white places a bishop on the corresponding diagonal entryway, then checkmate is very close. A key feature is that for white to place a white-square white bishop on the diagonal marked in red, it is immediate checkmate, whereas if black places a black-square black bishop on the blue diagonal, then checkmate comes three moves later.  The bishop cannon battery arrangement works because black threatens to release a bishop into the free region, and if white does not reply to those threats, then black will be three steps ahead, but otherwise, only two.

           The throne room

The rook towers are similar to the corresponding part of the previous $\omega^3$ position, and this is where white undertakes most of his main line progress towards checkmate.  Black will move the key bishop out as far as he likes on the first move, past $n$ rook towers, and the resulting position will have value $\omega^3\cdot n$.  These towers are each activated in turn, leading to a long series of play for white, interrupted at every opportunity by black causing a dramatic spectacle of forced-reply moves down in the bishop cannon battery.

Rook towers

            The rook towers

At every opportunity, black mounts a long distraction down in the bishop cannon battery.  Shown here is one bishop cannon. The cannonballs fire out of the cannon with force, in the sense that when each green bishop fires out, then white must reply by moving the guard pawns into place.

Bishop cannon

Bishop cannon

Upon firing, each bishop will position itself so as to attack the entrance diagonal of a long bishop gateway terminal wing.  This wing is arranged so that black can make a series of forced-reply threats successively, by moving to the attack squares (marked with the blue squares). Black is threatening to exit through the gateway doorway (in brown), but white can answer the threat by moving the white bishop guards (red) into position. Thus, each bishop coming out of a cannon (with force) can position itself at a gateway terminal of length $g$, making $g$ forced-reply moves in succession.  Since black can initiate firing with an arbitrarily large cannon, this means that at any moment, black can cause a forced-reply delay with game value $\omega^2$. Since the rook tower also has value $\omega^2$ by itself, the overall position has value $\omega^4=\omega^2\cdot\omega^2$.

Bishop gateway terminal wing

With future developments in mind, we found that one can make a more compact arrangement of the bishop cannon battery, freeing up a quarter board for perhaps another arrangement that might lead to a higher ordinal values.

Alternative compact version of bishop cannon battery

Read more about it in the article, which is available at the arxiv (pdf).

See also:

Open determinacy for class games

Posted on by
7

[bibtex key=GitmanHamkins2016:OpenDeterminacyForClassGames]

Abstract. The principle of open determinacy for class games — two-player games of perfect information with plays of length $\omega$, where the moves are chosen from a possibly proper class, such as games on the ordinals — is not provable in Zermelo-Fraenkel set theory ZFC or Godel-Bernays set theory GBC, if these theories are consistent, because provably in ZFC there is a definable open proper class game with no definable winning strategy. In fact, the principle of open determinacy and even merely clopen determinacy for class games implies Con(ZFC) and iterated instances Con(Con(ZFC)) and more, because it implies that there is a satisfaction class for first-order truth, and indeed a transfinite tower of truth predicates $\text{Tr}_\alpha$ for iterated truth-about-truth, relative to any class parameter. This is perhaps explained, in light of the Tarskian recursive definition of truth, by the more general fact that the principle of clopen determinacy is exactly equivalent over GBC to the principle of transfinite recursion over well-founded class relations. Meanwhile, the principle of open determinacy for class games is provable in the stronger theory GBC$+\Pi^1_1$-comprehension, a proper fragment of Kelley-Morse set theory KM.

See my earlier posts on part of this material:

 

A mathematician’s year in Japan

Posted on by
2

[bibtex key=Hamkins2015:AMathematiciansYearInJapan]

Years ago, when I was still a junior professor, I had the pleasure to live for a year in Japan, working as a research fellow at Kobe University. During that formative year, I recorded brief moments of my Japanese experience, and every two weeks or so—this was well before the current blogging era—I sent my descriptive missives by email to friends back home. I have now collected together those vignettes of my life in Japan, each a morsel of my experience. The book is now out!


A Mathematician's Year in Japan, by Joel David Hamkins, available on Amazon Kindle BooksA Mathematician’s Year in Japan
Joel David Hamkins

Glimpse into the life of a professor of logic as he fumbles his way through Japan.

A Mathematician’s Year in Japan is a lighthearted, though at times emotional account of how one mathematician finds himself in a place where everything seems unfamiliar, except his beloved research on the nature of infinity, yet even with that he experiences a crisis.

Available on Amazon $4.49.

Please be so kind as to write a review there.
jo eh ru

Ehrenfeucht’s lemma in set theory

Posted on by
2

[bibtex key=FuchsGitmanHamkins2018:EhrenfeuchtsLemmaInSetTheory]

This is joint work with Gunter Fuchs and Victoria Gitman. $\newcommand\HOD{\text{HOD}}\newcommand\Ehrenfeucht{\text{EL}}$

Abstract. Ehrenfeucht’s lemma asserts that whenever one element of a model of Peano arithmetic is definable from another, then they satisfy different types. We consider here the analogue of Ehrenfeucht’s lemma for models of set theory. The original argument applies directly to the ordinal-definable elements of any model of set theory, and in particular, Ehrenfeucht’s lemma holds fully for models of set theory satisfying $V=\HOD$. We show that the lemma can fail, however, in models of set theory with $V\neq\HOD$, and it necessarily fails in the forcing extension to add a generic Cohen real. We go on to formulate a scheme of natural parametric generalizations of Ehrenfeucht’s lemma, namely, the principles of the form $\Ehrenfeucht(A,P,Q)$, which asserts that whenever an object $b$ is definable in $M$ from some $a\in A$ using parameters in $P$, with $b\neq a$, then the types of $a$ and $b$ over $Q$ in $M$ are different. We also consider various analogues of Ehrenfeucht’s lemma obtained by using algebraicity in place of definability, where a set $b$ is \emph{algebraic} in $a$ if it is a member of a finite set definable from $a$ (as in J. D. Hamkins and C. Leahy, Algebraicity and implicit definability in set theory). Ehrenfeucht’s lemma holds for the ordinal-algebraic sets, we prove, if and only if the ordinal-algebraic and ordinal-definable sets coincide. Using similar analysis, we answer two open questions posed in my paper with Leahy, by showing that (i) algebraicity and definability need not coincide in models of set theory and (ii) the internal and external notions of being ordinal algebraic need not coincide.

Incomparable $\omega_1$-like models of set theory

Posted on by
1

[bibtex key=FuchsGitmanHamkins2017:IncomparableOmega1-likeModelsOfSetTheory]

This is joint work with Gunter Fuchs and Victoria Gitman.

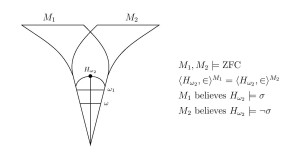
Abstract. We show that the analogues of the Hamkins embedding theorems, proved for the countable models of set theory, do not hold when extended to the uncountable realm of $\omega_1$-like models of set theory. Specifically, under the $\diamondsuit$ hypothesis and suitable consistency assumptions, we show that there is a family of $2^{\omega_1}$ many $\omega_1$-like models of $\text{ZFC}$, all with the same ordinals, that are pairwise incomparable under embeddability; there can be a transitive $\omega_1$-like model of ZFC that does not embed into its own constructible universe; and there can be an $\omega_1$-like model of PA whose structure of hereditarily finite sets is not universal for the $\omega_1$-like models of set theory.

In this article, we consider the question of whether the embedding theorems of my article, Every countable model of set theory embeds into its own constructible universe, which concern the countable models of set theory, might extend to the realm of uncountable models. Specifically, in that paper I had proved that (1) any two countable models of set theory are comparable by embeddability; indeed, (2) one countable model of set theory embeds into another just in case the ordinals of the first order-embed into the ordinals of the second; consequently, (3) every countable model of set theory embeds into its own constructible universe; and furthermore, (4) every countable model of set theory embeds into the hereditarily finite sets $\langle\text{HF},{\in}\rangle^M$ of any nonstandard model of arithmetic $M\models\text{PA}$. The question we consider here is, do the analogous results hold for uncountable models? Our answer is that they do not. Indeed, we shall prove that the corresponding statements do not hold even in the special case of $\omega_1$-like models of set theory, which otherwise among uncountable models often exhibit a special affinity with the countable models. Specifically, we shall construct large families of pairwise incomparable $\omega_1$-like models of set theory, even though they all have the same ordinals; we shall construct $\omega_1$-like models of set theory that do not embed into their own $L$; and we shall construct $\omega_1$-like models of \PA\ that are not universal for all $\omega_1$-like models of set theory.

The embedding theorems are expressed collectively in the theorem below. An embedding of one model $\langle M,{\in^M}\rangle$ of set theory into another $\langle N,{\in^N}\rangle$ is simply a function $j:M\to N$ for which $x\in^My\longleftrightarrow j(x)\in^Nj(y)$, for all $x,y\in M$, and in this case we say that $\langle M,{\in^M}\rangle$ embeds into $\langle N,{\in^N}\rangle$; note by extensionality that every embedding is injective. Thus, an embedding is simply an isomorphism of $\langle M,{\in^M}\rangle$ with its range, which is a submodel of $\langle N,{\in^N}\rangle$. Although this is the usual model-theoretic embedding concept for relational structures, the reader should note that it is a considerably weaker embedding concept than commonly encountered in set theory, because this kind of embedding need not be elementary nor even $\Delta_0$-elementary, although clearly every embedding as just defined is elementary at least for quantifier-free assertions. So we caution the reader not to assume a greater degree of elementarity beyond quantifier-free elementarity for the embeddings appearing in this paper.

Theorem.

1. For any two countable models of set theory $\langle M,\in^M\rangle$ and $\langle N,\in^N\rangle$, one of them embeds into the other.

2. Indeed, such an $\langle M,{\in^M}\rangle$ embeds into $\langle N,{\in^N}\rangle$ if and only if the ordinals of $M$ order-embed into the ordinals of $N$.

3. Consequently, every countable model $\langle M,\in^M\rangle$ of set theory embeds into its own constructible universe $\langle L^M,\in^M\rangle$.

4. Furthermore, every countable model of set theory embeds into the hereditary finite sets $\langle \text{HF},{\in}\rangle^M$ of any nonstandard model of arithmetic $M\models\text{PA}$. Indeed, $\text{HF}^M$ is universal for all countable acyclic binary relations.

One can begin to get an appreciation for the difference in embedding concepts by observing that ZFC proves that there is a nontrivial embedding $j:V\to V$, namely, the embedding recursively defined as follows $$j(y)=\bigl\{\ j(x)\ \mid\ x\in y\ \bigr\}\cup\bigl\{\{\emptyset,y\}\bigr\}.$$

We leave it as a fun exercise to verify that $x\in y\longleftrightarrow j(x)\in j(y)$ for the embedding $j$ defined by this recursion. (See my paper Every countable model of set theory embeds into its own constructible universe; but to give a hint here for the impatient, note that every $j(y)$ is nonempty and also $\emptyset\notin j(y)$; it follows that inside $j(y)$ we may identify the pair $\{\emptyset,y\}\in j(y)$; it follows that $j$ is injective and furthermore, the only way to have $j(x)\in j(y)$ is from $x\in y$.} Contrast this situation with the well-known Kunen inconsistency, which asserts that there can be no nontrivial $\Sigma_1$-elementary embedding $j:V\to V$. Similarly, the same recursive definition applied in $L$ leads to nontrivial embeddings $j:L\to L$, regardless of whether $0^\sharp$ exists. But again, the point is that embeddings are not necessarily even $\Delta_0$-elementary, and the familiar equivalence of the existence of $0^\sharp$ with a nontrivial “embedding” $j:L\to L$ actually requires a $\Delta_0$-elementary embedding.)

We find it interesting to note in contrast to the theorem above that there is no such embedding phenomenon in the the context of the countable models of Peano arithmetic (where an embedding of models of arithmetic is a function preserving all atomic formulas in the language of arithmetic). Perhaps the main reason for this is that embeddings between models of PA are automatically $\Delta_0$-elementary, as a consequence of the MRDP theorem, whereas this is not true for models of set theory, as the example above of the recursively defined embedding $j:V\to V$ shows, since this is an embedding, but it is not $\Delta_0$-elementary, in light of $j(\emptyset)\neq\emptyset$. For countable models of arithmetic $M,N\models\text{PA}$, one can show that there is an embedding $j:M\to N$ if and only if $N$ satisfies the $\Sigma_1$-theory of $M$ and the standard system of $M$ is contained in the standard system of $N$. It follows that there are many instances of incomparability. Meanwhile, it is a consequence of statement (4) that the embedding phenomenon recurs with the countable models of finite set theory $\text{ZFC}^{\neg\infty}$, that is, with $\langle\text{HF},{\in}\rangle^M$ for $M\models\text{PA}$, since all nonstandard such models are universal for all countable acyclic binary relations, and so in the context of countable models of $\text{ZFC}^{\neg\infty}$ there are precisely two bi-embeddability classes, namely, the standard model, which is initial, and the nonstandard countable models, which are universal.

Our main theorems are as follows.

Theorem.

1. If $\diamondsuit$ holds and ZFC is consistent, then there is a family $\mathcal C$ of $2^{\omega_1}$ many pairwise incomparable $\omega_1$-like models of ZFC, meaning that there is no embedding between any two distinct models in $\mathcal C$.

2. The models in statement (1) can be constructed so that their ordinals order-embed into each other and indeed, so that the ordinals of each model is a universal $\omega_1$-like linear order. If ZFC has an $\omega$-model, then the models of statement (1) can be constructed so as to have precisely the same ordinals.

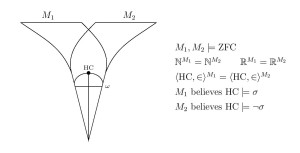
3. If $\diamondsuit$ holds and ZFC is consistent, then there is an $\omega_1$-like model $M\models\text{ZFC}$ and an $\omega_1$-like model $N\models\text{PA}$ such that $M$ does not embed into $\langle\text{HF},{\in}\rangle^N$.

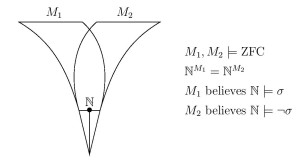
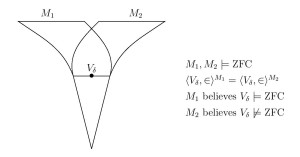
4. If there is a Mahlo cardinal, then in a forcing extension of $L$, there is a transitive $\omega_1$-like model $M\models\text{ZFC}$ that does not embed into its own constructible universe $L^M$.

Note that the size of the family $\mathcal C$ in statement (1) is as large as it could possibly be, given that any two elements in a pairwise incomparable family of structures must be non-isomorphic and there are at most $2^{\omega_1}$ many isomorphism types of $\omega_1$-like models of set theory or indeed of structures of size $\omega_1$ in any first-order finite language. Statement (2) shows that the models of the family $\mathcal C$ serve as $\omega_1$-like counterexamples to the assertion that one model of set theory embeds into another whenever the ordinals of the first order-embed into the ordinals of the second.

Large cardinals need not be large in HOD

Posted on by
1

[bibtex key=ChengFriedmanHamkins2015:LargeCardinalsNeedNotBeLargeInHOD]

Abstract. We prove that large cardinals need not generally exhibit their large cardinal nature in HOD. For example, a supercompact cardinal $\kappa$ need not be weakly compact in HOD, and there can be a proper class of supercompact cardinals in $V$, none of them weakly compact in HOD, with no supercompact cardinals in HOD. Similar results hold for many other types of large cardinals, such as measurable and strong cardinals.

In this article, we prove that large cardinals need not generally exhibit their large cardinal nature in HOD, the inner model of hereditarily ordinal-definable sets, and there can be a divergence in strength between the large cardinals of the ambient set-theoretic universe $V$ and those of HOD. Our general theme concerns the questions:

Questions.

1. To what extent must a large cardinal in $V$ exhibit its large cardinal properties in HOD?

2. To what extent does the existence of large cardinals in $V$ imply the existence of large cardinals in HOD?

For large cardinal concepts beyond the weakest notions, we prove, the answers are generally negative. In Theorem 4, for example, we construct a model with a supercompact cardinal that is not weakly compact in HOD, and Theorem 9 extends this to a proper class of supercompact cardinals, none of which is weakly compact in HOD, thereby providing some strongly negative instances of (1). The same model has a proper class of supercompact cardinals, but no supercompact cardinals in HOD, providing a negative instance of (2). The natural common strengthening of these situations would be a model with a proper class of supercompact cardinals, but no weakly compact cardinals in HOD. We were not able to arrange that situation, however, and furthermore it would be ruled out by Conjecture 13, an intriguing positive instance of (2) recently proposed by W. Hugh Woodin, namely, that if there is a supercompact cardinal, then there is a measurable cardinal in HOD. Many other natural possibilities, such as a proper class of measurable cardinals with no weakly compact cardinals in HOD, remain as open questions.

CUNY talk | Rutgers talk | Luminy talk

Strongly uplifting cardinals and the boldface resurrection axioms

Posted on by
1

[bibtex key=HamkinsJohnstone2017:StronglyUpliftingCardinalsAndBoldfaceResurrection]

Abstract. We introduce the strongly uplifting cardinals, which are equivalently characterized, we prove, as the superstrongly unfoldable cardinals and also as the almost hugely unfoldable cardinals, and we show that their existence is equiconsistent over ZFC with natural instances of the boldface resurrection axiom, such as the boldface resurrection axiom for proper forcing.

The strongly uplifting cardinals, which we introduce in this article, are a boldface analogue of the uplifting cardinals introduced in our previous paper, Resurrection axioms and uplifting cardinals, and are equivalently characterized as the superstrongly unfoldable cardinals and also as the almost hugely unfoldable cardinals. In consistency strength, these new large cardinals lie strictly above the weakly compact, totally indescribable and strongly unfoldable cardinals and strictly below the subtle cardinals, which in turn are weaker in consistency than the existence of $0^\sharp$. The robust diversity of equivalent characterizations of this new large cardinal concept enables constructions and techniques from much larger large cardinal contexts, such as Laver functions and forcing iterations with applications to forcing axioms. Using such methods, we prove that the existence of a strongly uplifting cardinal (or equivalently, a superstrongly unfoldable or almost hugely unfoldable cardinal) is equiconsistent over ZFC with natural instances of the boldface resurrection axioms, including the boldface resurrection axiom for proper forcing, for semi-proper forcing, for c.c.c. forcing and others. Thus, whereas in our prior article we proved that the existence of a mere uplifting cardinal is equiconsistent with natural instances of the (lightface) resurrection axioms, here we adapt both of these notions to the boldface context.

Definitions.

  • An inaccessible cardinal $\kappa$ is strongly uplifting if for every ordinal $\theta$ it is strongly $\theta$-uplifting, which is to say that for every $A\subset V_\kappa$ there is an inaccessible cardinal $\gamma\geq\theta$ and a set $A^*\subset V_\gamma$ such that $\langle V_\kappa,{\in},A\rangle\prec\langle V_\gamma,{\in},A^*\rangle$ is a proper elementary extension.
  • A cardinal $\kappa$ is superstrongly unfoldable, if for every ordinal $\theta$ it is superstrongly $\theta$-unfoldable, which is to say that for each $A\in H_{\kappa^+}$ there is a $\kappa$-model $M$ with $A\in M$ and a transitive set $N$ with an elementary embedding $j:M\to N$ with critical point $\kappa$ and $j(\kappa)\geq\theta$ and $V_{j(\kappa)}\subset N$.
  • A cardinal $\kappa$ is almost-hugely unfoldable, if for every ordinal $\theta$ it is almost-hugely $\theta$-unfoldable, which is to say that for each $A\in H_{\kappa^+}$ there is a $\kappa$-model $M$ with $A\in M$ and a transitive set $N$ with an elementary embedding $j:M\to N$ with critical point $\kappa$ and $j(\kappa)\geq\theta$ and $N^{<j(\kappa)}\subset N$.

Remarkably, these different-seeming large cardinal concepts turn out to be exactly equivalent to one another. A cardinal $\kappa$ is strongly uplifting if and only if it is superstrongly unfoldable, if and only if it is almost hugely unfoldable. Furthermore, we prove that the existence of such a cardinal is equiconsistent with several natural instances of the boldface resurrection axiom.

Theorem. The following theories are equiconsistent over ZFC.

  • There is a strongly uplifting cardinal.
  • There is a superstrongly unfoldable cardinal.
  • There is an almost hugely unfoldable cardinal.
  • The boldface resurrection axiom for all forcing.
  • The boldface resurrection axiom for proper forcing.
  • The boldface resurrection axiom for semi-proper forcing.
  • The boldface resurrection axiom for c.c.c. forcing.
  • The weak boldface resurrection axiom for countably-closed forcing, axiom-A forcing, proper forcing and semi-proper forcing, plus $\neg\text{CH}$.

 

 

Satisfaction is not absolute

Posted on by
22

[bibtex key=HamkinsYang:SatisfactionIsNotAbsolute]$\newcommand\N{\mathbb{N}}\newcommand\satisfies{\models}$

Abstract. We prove that the satisfaction relation $\mathcal{N}\satisfies\varphi[\vec a]$ of first-order logic is not absolute between models of set theory having the structure $\mathcal{N}$ and the formulas $\varphi$ all in common. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic $\langle\N,{+},{\cdot},0,1,{\lt}\rangle$, yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and the same arithmetic truths, yet disagree on their truths-about-truth, at any desired level of the iterated truth-predicate hierarchy; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have the same $\langle H_{\omega_2},{\in}\rangle$ or the same rank-initial segment $\langle V_\delta,{\in}\rangle$, yet disagree on which assertions are true in these structures.

On the basis of these mathematical results, we argue that a philosophical commitment to the determinateness of the theory of truth for a structure cannot be seen as a consequence solely of the determinateness of the structure in which that truth resides. The determinate nature of arithmetic truth, for example, is not a consequence of the determinate nature of the arithmetic structure $\N=\{ 0,1,2,\ldots\}$ itself, but rather, we argue, is an additional higher-order commitment requiring its own analysis and justification.

Many mathematicians and philosophers regard the natural numbers $0,1,2,\ldots\,$, along with their usual arithmetic structure, as having a privileged mathematical existence, a Platonic realm in which assertions have definite, absolute truth values, independently of our ability to prove or discover them. Although there are some arithmetic assertions that we can neither prove nor refute—such as the consistency of the background theory in which we undertake our proofs—the view is that nevertheless there is a fact of the matter about whether any such arithmetic statement is true or false in the intended interpretation. The definite nature of arithmetic truth is often seen as a consequence of the definiteness of the structure of arithmetic $\langle\N,{+},{\cdot},0,1,{\lt}\rangle$ itself, for if the natural numbers exist in a clear and distinct totality in a way that is unambiguous and absolute, then (on this view) the first-order theory of truth residing in that structure—arithmetic truth—is similarly clear and distinct.

Feferman provides an instance of this perspective when he writes (Feferman 2013, Comments for EFI Workshop, p. 6-7) :

In my view, the conception [of the bare structure of the natural numbers] is completely clear, and thence all arithmetical statements are definite.

It is Feferman’s `thence’ to which we call attention.  Martin makes a similar point (Martin, 2012, Completeness or incompleteness of basic mathematical concepts):

What I am suggesting is that the real reason for confidence in first-order completeness is our confidence in the full determinateness of the concept of the natural numbers.

Many mathematicians and philosophers seem to share this perspective. The truth of an arithmetic statement, to be sure, does seem to depend entirely on the structure $\langle\N,{+},{\cdot},0,1,{\lt}\rangle$, with all quantifiers restricted to $\N$ and using only those arithmetic operations and relations, and so if that structure has a definite nature, then it would seem that the truth of the statement should be similarly definite.

Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as $H_{\omega_2}$ or $V_\delta$, does not follow from the definite nature of the underlying structure in which that truth resides. Rather, we argue that the commitment to a theory of truth for a structure is a higher-order ontological commitment, going strictly beyond the commitment to a definite nature for the underlying structure itself.

We make our argument in part by proving that different models of set theory can have a structure identically in common, even the natural numbers, yet disagree on the theory of truth for that structure.

Theorem.

  • Two models of set theory can have the same structure of arithmetic $$\langle\N,{+},{\cdot},0,1,{\lt}\rangle^{M_1}=\langle\N,{+},{\cdot},0,1,{\lt}\rangle^{M_2},$$yet disagree on the theory of arithmetic truth.
  • Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is a well-order.
  • Two models of set theory that have the same natural numbers and the same reals, yet disagree on projective truth.
  • Two models of set theory can have a transitive rank initial segment in common $$\langle V_\delta,{\in}\rangle^{M_1}=\langle V_\delta,{\in}\rangle^{M_2},$$yet disagree about whether it is a model of ZFC.

The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.

 

The foundation axiom and elementary self-embeddings of the universe

Posted on by
9

[bibtex key=DaghighiGolshaniHaminsJerabek2013:TheFoundationAxiomAndElementarySelfEmbeddingsOfTheUniverse]$\newcommand\ZFC{\text{ZFC}}\newcommand\ZFCf{\ZFC^{\rm-f}}\newcommand\AFA{\text{AFA}}\newcommand\BAFA{\text{BAFA}}$

Festschrift celebrating 60th birthdays of Peter Koepke and Philip Welch
In this article, we examine the role played by the axiom of foundation in the well-known Kunen inconsistency, the theorem asserting that there is no nontrivial elementary embedding of the set-theoretic universe to itself. All the standard proofs of the Kunen inconsistency make use of the axiom of foundation (see Kanamori’s books and also Generalizations of the Kunen inconsistency), and this use is essential, assuming that $\ZFC$ is consistent, because as we shall show there are models of $\ZFCf$ that admit nontrivial elementary self-embeddings and even nontrivial definable automorphisms. Meanwhile, a fragment of the Kunen inconsistency survives without foundation as the claim in $\ZFCf$ that there is no nontrivial elementary self-embedding of the class of well-founded sets. Nevertheless, some of the commonly considered anti-foundational theories, such as the Boffa theory $\BAFA$, prove outright the existence of nontrivial automorphisms of the set-theoretic universe, thereby refuting the Kunen assertion in these theories.  On the other hand, several other common anti-foundational theories, such as Aczel’s anti-foundational theory $\ZFCf+\AFA$ and Scott’s theory $\ZFCf+\text{SAFA}$, reach the opposite conclusion by proving that there are no nontrivial elementary embeddings from the set-theoretic universe to itself. Our summary conclusion, therefore, is that the resolution of the Kunen inconsistency in set theory without foundation depends on the specific nature of one’s anti-foundational stance.

This is joint work with Ali Sadegh Daghighi, Mohammad Golshani, myself and Emil Jeřábek, which grew out of our interaction on Ali’s question on MathOverflow, Is there any large cardinal beyond the Kunen inconsistency?

Resurrection axioms and uplifting cardinals

Posted on by
2

[bibtex key=HamkinsJohnstone2014:ResurrectionAxiomsAndUpliftingCardinals]

Abstract. We introduce the resurrection axioms, a new class of forcing axioms, and the uplifting cardinals, a new large cardinal notion, and prove that various instances of the resurrection axioms are equiconsistent over ZFC with the existence of uplifting cardinal.

Many classical forcing axioms can be viewed, at least informally, as the claim that the universe is existentially closed in its forcing extensions, for the axioms generally assert that certain kinds of filters, which could exist in a forcing extension $V[G]$, exist already in $V$. In several instances this informal perspective is realized more formally: Martin’s axiom is equivalent to the assertion that $H_{\frak{c}}$ is existentially closed in all c.c.c. forcing extensions of the universe, meaning that $H_{\frak{c}}\prec_{\Sigma_1}V[G]$ for all such extensions; the bounded proper forcing axiom is equivalent to the assertion that $H_{\omega_2}$ is existentially closed in all proper forcing extensions, or $H_{\omega_2}\prec_{\Sigma_1}V[G]$; and there are other similar instances.

In model theory, a submodel $M\subset N$ is existentially closed in $N$ if existential assertions true in $N$ about parameters in $M$ are true already in $M$, that is, if $M$ is a $\Sigma_1$-elementary substructure of $N$, which we write as $M\prec_{\Sigma_1} N$. Furthermore, in a general model-theoretic setting, existential closure is tightly connected with resurrection, the theme of this article.

Elementary Fact. If $\mathcal{M}$ is a submodel of $\mathcal{N}$, then the following are equivalent.

  1. The model $\mathcal{M}$ is existentially closed in $\mathcal{N}$.
  2. $\mathcal{M}\subset \mathcal{N}$ has resurrection. That is, there is a further extension $\mathcal{M}\subset\mathcal{N}\subset\mathcal{M}^+$ for which $\mathcal{M}\prec\mathcal{M}^+$.

We call this resurrection because although certain truths in $\mathcal{M}$ may no longer hold in the extension $\mathcal{N}$, these truths are nevertheless revived in light of $\mathcal{M}\prec\mathcal{M}^+$ in the further extension to $\mathcal{M}^+$.

In the context of forcing axioms, we are more interested in the case of forcing extensions than in the kind of arbitrary extension $\mathcal{M}^+$ arising in the fact, and in this context the equivalence of (1) and (2) breaks own, although the converse implication $(2)\to(1)$ always holds, and every instance of resurrection implies the corresponding instance of existential closure. This key observation leads us to the main unifying theme of this article, the idea that

resurrection may allow us to formulate more robust forcing axioms 

than existential closure or than combinatorial assertions about filters and dense sets. We therefore introduce in this paper a spectrum of new forcing axioms utilizing the resurrection concept.

Main Definition. Let $\Gamma$ be a fixed definable class of forcing notions.

  1. The resurrection axiom $\text{RA}(\Gamma)$ is the assertion that for every forcing notion $\mathbb{Q}\in\Gamma$ there is further forcing $\mathbb{R}$, with $\vdash_{\mathbb{Q}}\mathbb{R}\in\Gamma$, such that if $g\ast h\subset\mathbb{Q}\ast\mathbb{R}$ is $V$-generic, then $H_{\frak{c}}\prec H_{\frak{c}}^{V[g\ast h]}$.
  2. The weak resurrection axiom $\text{wRA}(\Gamma)$ is the assertion that for every $\mathbb{Q}\in\Gamma$ there is further forcing $\mathbb{R}$, such that if $g\ast h\subset\mathbb{Q}\ast\mathbb{R}$ is $V$-generic, then $H_{\frak{c}}\prec H_{\frak{c}}^{V[g\ast h]}$.

The main result is to prove that various formulations of the resurrection axioms are equiconsistent with the existence of an uplifting cardinal, where an inaccessible cardinal $\kappa$ is uplifting, if there are arbitrarily large inaccessible cardinals $\gamma$ for which $H_\kappa\prec H_\gamma$.  This is a rather weak large cardinal notion, having consistency strength strictly less than the existence of a Mahlo cardinal, which is traditionally considered to be very low in the large cardinal hierarchy.  One highlight of the article is our development of “the world’s smallest Laver function,” the Laver function concept for uplifting cardinals, and we perform an analogue of the Laver preparation in order to achieve the resurrection axiom for c.c.c. forcing.

Main Theorem. The following theories are equiconsistent over ZFC:

  1. There is an uplifting cardinal.
  2. $\text{RA}(\text{all})$.
  3. $\text{RA}(\text{ccc})$.
  4. $\text{RA}(\text{semiproper})+\neg\text{CH}$.
  5. $\text{RA}(\text{proper})+\neg\text{CH}$.
  6. For some countable ordinal $\alpha$, the axiom $\text{RA}(\alpha\text{-proper})+\neg\text{CH}$.
  7. $\text{RA}(\text{axiom-A})+\neg\text{CH}$.
  8. $\text{wRA}(\text{semiproper})+\neg\text{CH}$.
  9. $\text{wRA}(\text{proper})+\neg\text{CH}$.
  10. For some countable ordinal $\alpha$, the axiom $\text{wRA}(\alpha\text{-proper})+\neg\text{CH}$.
  11. $\text{wRA}(\text{axiom-A})+\neg\text{CH}$.
  12. $\text{wRA}(\text{countably closed})+\neg\text{CH}$.

The proof outline proceeds in two directions: on the one hand, the resurrection axioms generally imply that the continuum $\frak{c}$ is uplifting in $L$; and conversely, given any uplifting cardinal $\kappa$, we may perform a suitable lottery iteration of $\Gamma$ forcing to obtain the resurrection axiom for $\Gamma$ in a forcing extension with $\kappa=\frak{c}$.

In a follow-up article, currently nearing completion, we treat the boldface resurrection axioms, which allow a predicate $A\subset\frak{c}$ and ask for extensions of the form $\langle H_{\frak{c}},{\in},A\rangle\prec\langle H_{\frak{c}}^{V[g\ast h]},{\in},A^\ast\rangle$, for some $A^\ast\subset\frak{c}^{V[g\ast h]}$ in the extension.  In that article, we prove the equiconsistency of various formulations of boldface resurrection with the existence of a strongly uplifting cardinal, which we prove is the same as a superstrongly unfoldable cardinal.