This will be a plenary talk for the Chinese Annual Conference on Mathematical Logic (CACML 2020), held online 13-15 November 2020. My talk will be held 14 November 17:00 Beijing time (9 am GMT).

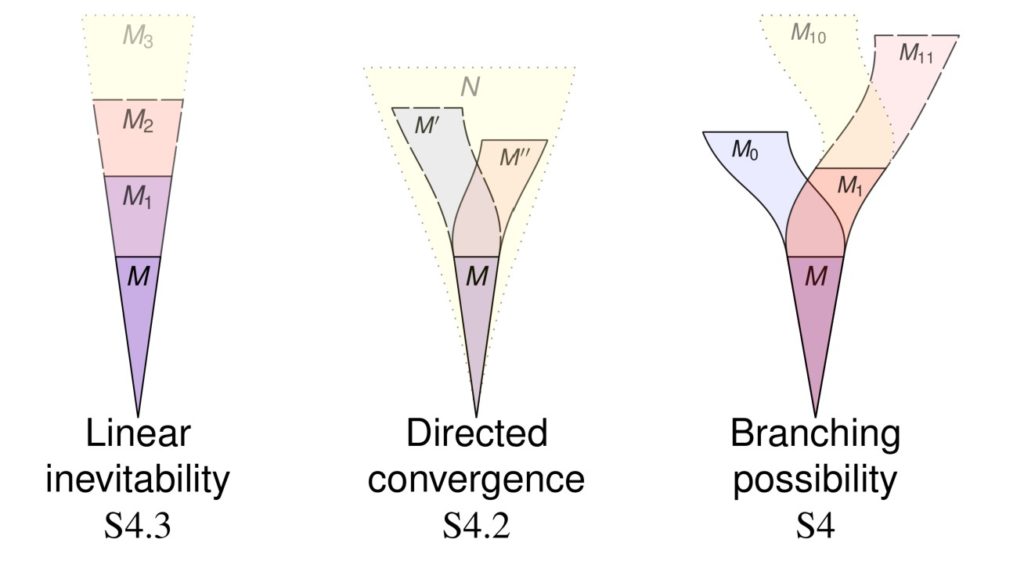
Abstract. Recent years have seen a flurry of mathematical activity in set-theoretic and arithmetic potentialism, in which we investigate a collection of models under various natural extension concepts. These potentialist systems enable a modal perspective—a statement is possible in a model, if it is true in some extension, and necessary, if it is true in all extensions. We consider the models of ZFC set theory, for example, with respect to submodel extensions, rank-extensions, forcing extensions and others, and these various extension concepts exhibit different modal validities. In this talk, I shall describe the state of current developments, including the most recent tools and results.