1. [bibtex key=”GitmanHamkinsKaragila:KM-set-theory-does-not-prove-the-class-Fodor-theorem”]

Abstract.
We show that Kelley-Morse (KM) set theory does not prove the class Fodor principle, the assertion that every regressive class function $F:S\to\newcommand\Ord{\text{Ord}}\Ord$ defined on a stationary class $S$ is constant on a stationary subclass. Indeed, it is relatively consistent with KM for any infinite $\lambda$ with $\omega\leq\lambda\leq\Ord$ that there is a class function $F:\Ord\to\lambda$ that is not constant on any stationary class. Strikingly, it is consistent with KM that there is a class $A\subseteq\omega\times\Ord$, such that each section $A_n=\{\alpha\mid (n,\alpha)\in A\}$ contains a class club, but $\bigcap_n A_n$ is empty. Consequently, it is relatively consistent with KM that the class club filter is not $\sigma$-closed.

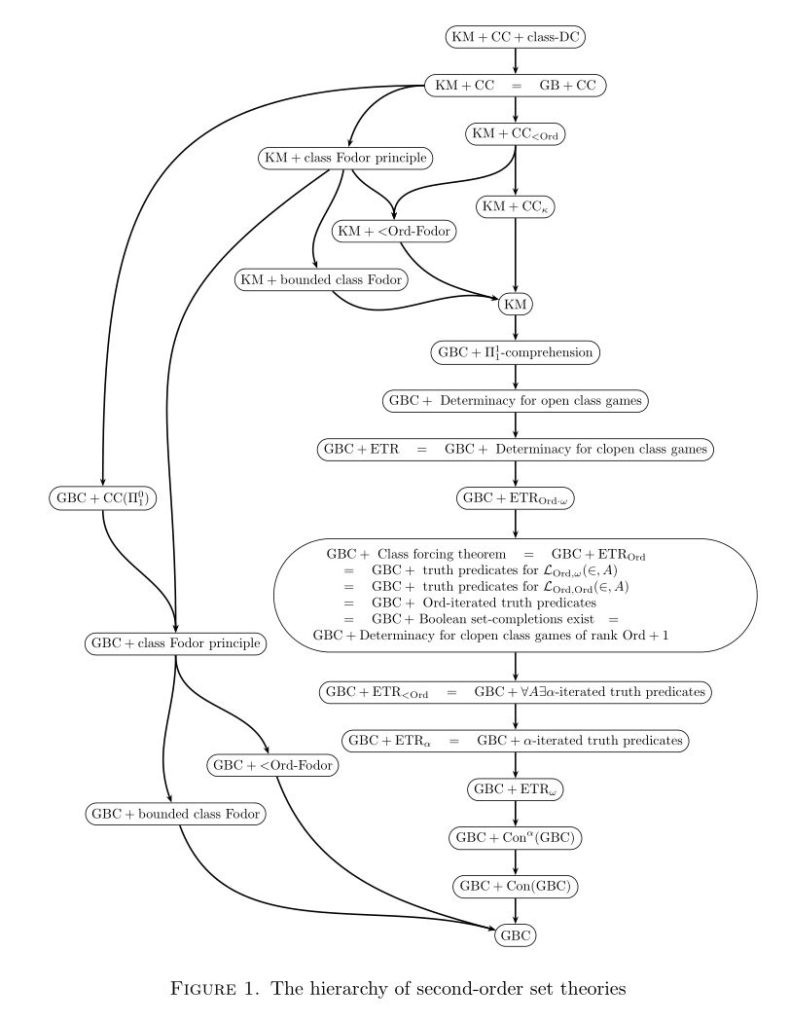
The class Fodor principle is the assertion that every regressive class function $F:S\to\Ord$ defined on a stationary class $S$ is constant on a stationary subclass of $S$. This statement can be expressed in the usual second-order language of set theory, and the principle can therefore be sensibly considered in the context of any of the various second-order set-theoretic systems, such as Gödel-Bernays (GBC) set theory or Kelley-Morse (KM) set theory. Just as with the classical Fodor’s lemma in first-order set theory, the class Fodor principle is equivalent, over a weak base theory, to the assertion that the class club filter is normal. We shall investigate the strength of the class Fodor principle and try to find its place within the natural hierarchy of second-order set theories. We shall also define and study weaker versions of the class Fodor principle.

If one tries to prove the class Fodor principle by adapting one of the classical proofs of the first-order Fodor’s lemma, then one inevitably finds oneself needing to appeal to a certain second-order class-choice principle, which goes beyond the axiom of choice and the global choice principle, but which is not available in Kelley-Morse set theory. For example, in one standard proof, we would want for a given $\Ord$-indexed sequence of non-stationary classes to be able to choose for each member of it a class club that it misses. This would be an instance of class-choice, since we seek to choose classes here, rather than sets. The class choice principle $\text{CC}(\Pi^0_1)$, it turns out, is sufficient for us to make these choices, for this principle states that if every ordinal $\alpha$ admits a class $A$ witnessing a $\Pi^0_1$-assertion $\varphi(\alpha,A)$, allowing class parameters, then there is a single class $B\subseteq \Ord\times V$, whose slices $B_\alpha$ witness $\varphi(\alpha,B_\alpha)$; and the property of being a class club avoiding a given class is $\Pi^0_1$ expressible.

Thus, the class Fodor principle, and consequently also the normality of the class club filter, is provable in the relatively weak second-order set theory $\text{GBC}+\text{CC}(\Pi^0_1)$. This theory is known to be weaker in consistency strength than the theory $\text{GBC}+\Pi^1_1$-comprehension, which is itself strictly weaker in consistency strength than KM.

But meanwhile, although the class choice principle is weak in consistency strength, it is not actually provable in KM; indeed, even the weak fragment $\text{CC}(\Pi^0_1)$ is not provable in KM. Those results were proved several years ago by the first two authors, but they can now be seen as consequences of the main result of this article (see corollary 15. In light of that result, however, one should perhaps not have expected to be able to prove the class Fodor principle in KM.

Indeed, it follows similarly from arguments of the third author in his dissertation that if $\kappa$ is an inaccessible cardinal, then there is a forcing extension $V[G]$ with a symmetric submodel $M$ such that $V_\kappa^M=V_\kappa$, which implies that $\mathcal M=(V_\kappa,\in, V^M_{\kappa+1})$ is a model of Kelley-Morse, and in $\mathcal M$, the class Fodor principle fails in a very strong sense.

In this article, adapting the ideas of Karagila to the second-order set-theoretic context and using similar methods as in Gitman and Hamkins’s previous work on KM, we shall prove that every model of KM has an extension in which the class Fodor principle fails in that strong sense: there can be a class function $F:\Ord\to\omega$, which is not constant on any stationary class. In particular, in these models, the class club filter is not $\sigma$-closed: there is a class $B\subseteq\omega\times\Ord$, each of whose vertical slices $B_n$ contains a class club, but $\bigcap B_n$ is empty.

Main Theorem. Kelley-Morse set theory KM, if consistent, does not prove the class Fodor principle. Indeed, if there is a model of KM, then there is a model of KM with a class function $F:\Ord\to \omega$, which is not constant on any stationary class; in this model, therefore, the class club filter is not $\sigma$-closed.

We shall also investigate various weak versions of the class Fodor principle.

Definition.

1. For a cardinal $\kappa$, the class $\kappa$-Fodor principle asserts that every class function $F:S\to\kappa$ defined on a stationary class $S\subseteq\Ord$ is constant on a stationary subclass of $S$.
2. The class ${<}\Ord$-Fodor principle is the assertion that the $\kappa$-class Fodor principle holds for every cardinal $\kappa$.
3. The bounded class Fodor principle asserts that every regressive class function $F:S\to\Ord$ on a stationary class $S\subseteq\Ord$ is bounded on a stationary subclass of $S$.
4. The very weak class Fodor principle asserts that every regressive class function $F:S\to\Ord$ on a stationary class $S\subseteq\Ord$ is constant on an unbounded subclass of $S$.

We shall separate these principles as follows.

Theorem. Suppose KM is consistent.

1. There is a model of KM in which the class Fodor principle fails, but the class ${<}\Ord$-Fodor principle holds.
2. There is a model of KM in which the class $\omega$-Fodor principle fails, but the bounded class Fodor principle holds.
3. There is a model of KM in which the class $\omega$-Fodor principle holds, but the bounded class Fodor principle fails.
4. $\text{GB}^-$ proves the very weak class Fodor principle.

Finally, we show that the class Fodor principle can neither be created nor destroyed by set forcing.

Theorem. The class Fodor principle is invariant by set forcing over models of $\text{GBC}^-$. That is, it holds in an extension if and only if it holds in the ground model.

Let us conclude this brief introduction by mentioning the following easy negative instance of the class Fodor principle for certain GBC models. This argument seems to be a part of set-theoretic folklore. Namely, consider an $\omega$-standard model of GBC set theory $M$ having no $V_\kappa^M$ that is a model of ZFC. A minimal transitive model of ZFC, for example, has this property. Inside $M$, let $F(\kappa)$ be the least $n$ such that $V_\kappa^M$ fails to satisfy $\Sigma_n$-collection. This is a definable class function $F:\Ord^M\to\omega$ in $M$, but it cannot be constant on any stationary class in $M$, because by the reflection theorem there is a class club of cardinals $\kappa$ such that $V_\kappa^M$ satisfies $\Sigma_n$-collection.

Read more by going to the full article: [bibtex key=”GitmanHamkinsKaragila:KM-set-theory-does-not-prove-the-class-Fodor-theorem”]