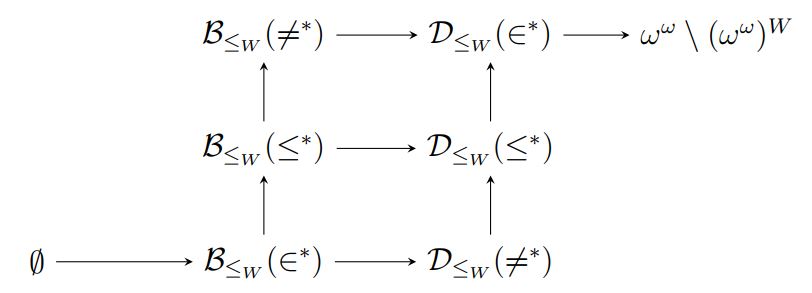Tag Archives: Corey Bachal Switzer

Corey Bacal Switzer, PhD 2020, CUNY Graduate Center

Posted on by
Reply

Dr. Corey Bacal Switzer successfully defended his PhD dissertation, entitled “Alternative Cichoń Diagrams and Forcing Axioms Compatible with CH,” on 31 July 2020, for the degree of PhD from The Graduate Center of the City University of New York. The dissertation was supervised jointly by myself and Gunter Fuchs.

Corey has now accepted a three-year post-doctoral research position at the University of Vienna, where he will be working with Vera Fischer.

Corey Bacal Switzer | arXiv.org | Google scholar | dissertation

Abstract. This dissertation surveys several topics in the general areas of iterated forcing, infinite combinatorics and set theory of the reals. There are four largely independent chapters, the first two of which consider alternative versions of the Cichoń diagram and the latter two consider forcing axioms compatible with CH . In the first chapter, I begin by introducing the notion of a reduction concept , generalizing various notions of reduction in the literature and show that for each such reduction there is a Cichoń diagram for effective cardinal characteristics relativized to that reduction. As an application I investigate in detail the Cichoń diagram for degrees of constructibility relative to a fixed inner model $W\models\text{ZFC}$.

In the second chapter, I study the space of functions $f:\omega^\omega\to\omega^\omega$ and introduce 18 new higher cardinal characteristics associated with this space. I prove that these can be organized into two diagrams of 6 and 12 cardinals respecitvely analogous to the Cichoń diagram on $\omega$. I then investigate their relation to cardinal invariants on ω and introduce several new forcing notions for proving consistent separations between the cardinals. The third chapter concerns Jensen’s subcomplete and subproper forcing. I generalize these notions to the (seemingly) larger classes of ∞-subcomplete and ∞-subproper. I show that both classes are (apparently) much more nicely behaved structurally than their non-∞-counterparts and iteration theorems are proved for both classes using Miyamoto’s nice iterations. Several preservation theorems are then presented. This includes the preservation of Souslin trees, the Sacks property, the Laver property, the property of being $\omega^\omega$-bounding and the property of not adding branches to a given $\omega_1$-tree along nice iterations of ∞-subproper forcing notions. As an application of these methods I produce many new models of the subcomplete forcing axiom, proving that it is consistent with a wide variety of behaviors on the reals and at the level of $\omega_1$.

The final chapter contrasts the flexibility of SCFA with Shelah’s dee-complete forcing and its associated axiom DCFA . Extending a well known result of Shelah, I show that if a tree of height $\omega_1$ with no branch can be embedded into an $\omega_1$-tree, possibly with branches, then it can be specialized without adding reals. As a consequence I show that DCFA implies there are no Kurepa trees, even if CH fails.

Corey Switzer, The Cichoń Diagram for Degrees of Relative Constructibility

Posted on by
1

My student Corey Switzer has just completed a paper:


Corey Switzer, The Cichoń Diagram for Degrees of Relative Constructibility, ArXiv e-print:1801.06497.

 

Abstract. Following a line of research initiated in Brendle/Brooke-Taylor/Ng/Nies, I describe a general framework for turning reduction concepts of relative computability into diagrams forming an analogy with the Cichoń diagram for cardinal characteristics of the continuum. I show that working from relatively modest assumptions about a notion of reduction, one can construct a robust version of such a diagram. As an application, I define and investigate the Cichoń Diagram for degrees of constructibility relative to a fixed inner model W. Many analogies hold with the classical theory as well as some surprising differences. Along the way I introduce a new axiom stating, roughly, that the constructibility diagram is as complex as possible.

This interesting paper concerns a generalization of the Cichoń diagram to arbitrary reducibility notions, focussing on the case of the constructibility degrees, or somewhat more generally, relative constructibility $\leq_W$ over a fixed inner model $W$.

The classes are defined by an abstract generalization of the ideas underlying the familiar cardinal characteristics and the classical Cichoń diagram. Namely, $B_{\leq}(R)$ is the set of reals that $\leq$-build a witness for the fact that the reals of $W$ are small with respect to the relation $R$, that is, an $R$-bound for the reals of $W$; and $D_{\leq}(R)$ is the set of reals that $\leq$-build a witness for the fact that the reals of $W$ are not big with respect to the relation $R$, that is, a real that is not $R$-dominated by any real in $W$.

These classes fit together in a way that forms a robust analogy with the classical Cichoń diagram.

In his paper, Corey proves that the diagram is complete with respect to the inclusions indicated, by analyzing the nature of the diagram in various forcing extensions of $W$, such as the following.

 

In the end, he shows that in a suitable (proper) forcing extension, one can achieve all the separations simultaneously.

Indeed, the assertion that all separations are attained can be taken as a set-theoretic principle or axiom of its own, the complete Cichoń diagram assertion CD. He proves, for example, that CD is a consequence of the maximality principle.

See Corey’s blog post about his paper.