This will be a talk for the Dartmouth Logic Seminar on January 23rd, 2014.
Abstract. I will discuss a number of theorems showing that the satisfaction relation of first-order logic is less absolute than might have been supposed. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic $\langle\mathbb{N},{+},{\cdot},0,1,{\lt}\rangle$, yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $\langle V_\delta,{\in}\rangle$ in common, yet disagree about whether it is a model of ZFC. The theorems are proved with elementary classical model-theoretic methods, and many of them can be considered folklore results in the subject of models of arithmetic.
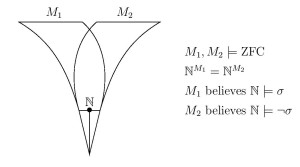On the basis of these mathematical results, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.
Main article: Satisfaction is not absolute
