This will be a talk for the Notre Dame Logic Seminar, 3 December 2024, 2:00pm, 125 Hayes-Healey.

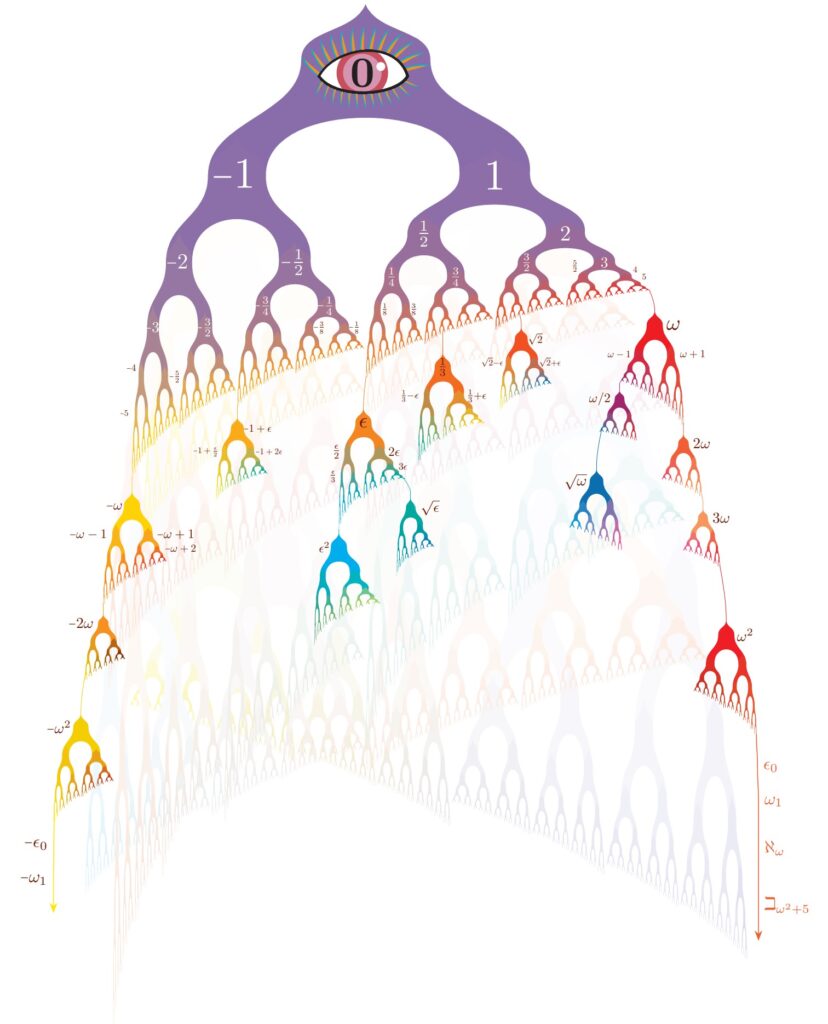
Abstract. I shall give an account of the theory of computable surreal numbers, proving that these form a real-closed field. Which real numbers arise as computable surreal numbers? You may be surprised to learn that some noncomputable real numbers have computable surreal presentations, and indeed the computable surreal real numbers are exactly the hyperarithmetic reals. More generally, the computable surreal numbers are exactly those with a hyperarithmetic surreal sign sequence. This is joint work with Dan Turetsky, but we subsequently found that it is a rediscovery of earlier work of Jacob Lurie.

Lecture notes:

See related MathOverflow posts:

• What do we know about the computable surreal numbers?
• Which are the hereditarily computably enumerable sets?

Also see my elementary introduction to the surreal numbers: The surreal numbers