Consider this fascinating vision of recursive chess — the etching below was created by Django Pinter, a tutorial student of mine who has just completed his degree in the PPL course here at Oxford, given to me as a parting gift at the conclusion of his studies. Django’s idea was to play chess, but in order for a capture to occur successfully on the board, as here with the black Queen attempting to capture the opposing white knight, the two pieces would themselves sit down for their own game of (recursive) chess. The idea was that the capture would be successful only in the event that the subgame was won. Notice in the image that not only is there a smaller recursive game of chess, but also a still tinier subrecursive game below that (if you inspect closely), while at the same time larger pieces loom in the background, indicating that the main board itself is already several levels deep in the recursion.

The recursive chess idea may seem clear enough initially, and intriguing. But with further reflection, we might wonder how does it work exactly? What precisely is the game of recursive chess? This is my question here.
My goal with this post is to open a discussion about what ultimately should be the precise the rules and operations of recursive chess. I’m not completely sure what the best rule set will be, although I do offer several proposals here. I welcome further proposals, commentary, suggestions, and criticism about how to proceed. Once we settle upon a best or most natural version of the game, then I shall hope perhaps to prove things about it. Will you help me decide what is the game of recursive chess?
Let me describe several natural proposals:
Naïve recursion. Although this seems initially to be a simple, sound proposal, ultimately I find it problematic. The naïve idea is that when one piece wants to capture another in the game at hand, then the two pieces themselves play a game of chess, starting from the usual chess starting position. I would find it natural that the attacking piece should play as white in this game, going first, and if that player wins the subgame, then the capture in the current game is successful. If the subgame is a loss, then the capture is unsuccessful.
There seem, however, to be a variety of ways to handle the losing subgame outcome, and since these will apply with several of the other proposals, let me record them here:
- Failed-capture. If the subgame is lost, then the capture in the current game simply does not occur. Both pieces remain on their original squares, and the turn of play passes to the opponent. Notice that this will have serious affects in certain chess situations involving zugzwang, a position where a player has no good move — because if one of them is a capture, then the player can aim to play badly in the subgame and thereby legally pass the turn of play to the opponent without having made any move. This situation will in effect cause the subgame players to attempt to lose, rather than win, which seems undesirable.
- Failed-capture-with-penalty. If the subgame is lost, then the capture does not occur, but furthermore, the attacking piece is itself lost, removed from the board, and the turn of play passes to the opponent. In effect, under this rule, every attempt at capture is putting the life of the capturing piece at risk, which makes a certain amount of sense from a military point of view. I think perhaps this is a good rule.
- Failed-capture-with-retry. If the subgame is lost, then the capture does not occur, but both pieces remain on their original squares, and the attacking player is allowed to proceed with another (different) move. Attempting the same attack from the same board position multiple times is subject to the three-fold repetition rule. This interpretation amounts in effect to the game play searching a large part of the game tree, exploring the possible capturing moves, but with the first successful option fixed as official. It invites manipulation by the opponent, who might play badly against a misguided capture attempt, causing it to be fixed as the official move.
- Drawn subgame. A further complication arises from the fact that the subgame can itself be drawn, rather than won. Is this sufficient to cause the penalty or the retry? Or does this count as a failed capture?
As I see it, however, the principal problem with the naïve recursion rule is that it seems to be ill-founded. After all, we can have a game with a capture, which leads to a subgame with a capture, which leads to a deeper subgame with a capture, and so on descending forever. How is the outcome determined in this infinitely descending situation? None of the subgames is ever resolved with a definite conclusion until all of them are, and there seems no coherent way to assign resolutions to them. All infinitely many subgames are simply left hanging mid-play, and indeed mid-move. For this reason, the naïve recursion idea seems ultimately incoherent to me as a game rule.
What we would seem to need instead is a well-founded recursion, one which would ultimately bottom-out in a base case. With such a recursion, every outcome of the game would be well-defined. Such a well-founded recursion would be achieved, for example, if on every subgame there were strictly fewer pieces. Eventually, the subgames would reduce to king versus king, a drawn game, and then the drawn subgame rule would be invoked to whatever affect it cause. But the recursion would definitely terminate. And perhaps most recursions would terminate because the stronger player was ultimately mating in all his attacks, without requiring any invocation of the drawn subgame rule.
We can easily describe several natural subgame positions with one fewer piece. For example, when one piece attacks another, we may naturally consider the positions that would result if we performed the capture, or if we removed the attacking piece; and we might further consider swapping the roles of the players in these positions. Such cases would constitute a well-founded recursion, because the subgame position would have fewer pieces than the main position. In this way, we arrive at several natural recursion rules for recursive chess.
Proof-of-sufficiency recursion. The motivating idea of this recursion rule is that in order for an attack to be successful, the attacking player must prove that it will be sufficient for the attack to be successful. So, when piece A attacks piece B in the game, then a subgame is set up from the position that would result if A were successfully to capture B, and the players proceed in the game in which the attack has occurred. This is the same as proceeding in the main game, under the assumption that the attack was successful. If the attacking player can win this subgame, then it shows in a sense the sufficiency of the attack as a means to win, and so on the proof-of-sufficiency idea, we allow this as a reason for the attack to have been successful.
One might object that this recursion seems at first to amount to just playing chess as usual, since the subgame is the same as the original game with the attack having succeeded. But there is a subtle difference. For a misguided attack, the attacked player can play suboptimally in the subgame, intentionally losing that game, and then play differently in the main game. There is, of course, no obligation that the players respond the same at the higher-level games as in the lower games, and this is all part of their strategic calculation.
Proof-of-necessity recursion. The motivating idea of this recursion rule, in contrast, is that in order for an attack to be successful, the attacking player must prove that it is necessary that the attack take place. When piece A attacks piece B in the main game, then a subgame is set up in which the attack has not succeeded, but instead the attacking piece is lost, but the color sides of the players are swapped. If a black Queen attacks a white knight, for example, then in the subgame position, the queen is removed, and the players proceed from that positions, but with the opposite colors. By winning this subgame, the attacking player is in effect demonstrating that if the attack were to fail, then it would be devastating for them. In other words, they are demonstrating the necessity of the success of the attack.
For the both the proof-of-sufficiency and the proof-of-necessity versions of the recursion, it seems to me that any of the three failed-capture rules would be sensible. And so we have quite a few different interpretations here for what is the game of recursive chess.
What is your proposal? Please let me know in the comments. I am interested to hear any comments or criticism.


How about the 3-fold repetition rule applies to all active chess games and not just the current layer? And instead of starting with the standard board, you play Fisher random chess so there are many(but finite) possible active states allowed.
My first thought is to do naive recursion, but have each game be tagged with an ordinal. Subgames must be given smaller ordinals, and then 0-games are played out as standard chess. My inclination is to let the defending player choose the ordinal of the subgame.
I had had the same idea before I had come to the realization that we can achieve a well-founded recursion simply by having subgames with fewer pieces, which seems both simpler and more natural to me than involving the ordinals. My idea had been perhaps to start from the standard chess opening, but with an ordinal—is this also what you had in mind?
Here are some thoughts.
I like the idea of Failed-capture-with-penalty, because it really changes the way chess works. Here are the versions that I can imagine:
1. In the subgame, we remove the two confronting pieces (if they play chess, they cannot be chess pieces), and each player keeps his side. It means for example that at the beginning of the game, it is a lot more dangerous to take a pawn with a queen, which I think is interesting. We can also do a variant where they also must swap sides, and in this case at the contrary it is difficult to take a strong piece with a weaker one, and it also means that if your position is a lot better than the one of your opponent, it is in fact harder to extend your advantage.
2. In the subgame, the piece is actually captured, but the players switch places. The way to interpret it is that the attacker cannot capture a piece if it makes to easy to win afterwards. He needs to give some hope to the other player. Again, if you have a big advantage, it is more dangerous to capture pieces.
3. At each capture, we choose at random if we do a subgame, with a probability of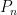 at the level
at the level 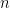 . The subgame begins with the usual position of a chess game. If
. The subgame begins with the usual position of a chess game. If 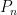 tends sufficiently quickly to 0 (for example I think that
tends sufficiently quickly to 0 (for example I think that 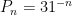 works), the probability that the game will end at some point is equal to 1. What I like with this version is that it doesn’t put an upper bound on the depth of the game.
works), the probability that the game will end at some point is equal to 1. What I like with this version is that it doesn’t put an upper bound on the depth of the game.
I really like some of these ideas! Thank you very much.
I don’t think the idea is that the pieces are playing with little pieces no I think that the one on the left is ensuring the correct behaviour of the piece on the right through an unseen player (x) in opposition will h a known unknown – the castle/pawn. If (as the image suggests) both ‘sides’ are made up of black AND white pieces, are they playing a game of naive recursion or engaging in a performative demo of sorts, to determine the position of the white bishop that occupies the white squares (not the one occupying the black shown in the image). If so one could infer the game will never be repeated due to the unique skill set of each piece.
What a wonderful question!
Here’s one idea that tries to stay as close as possible to classical chess. The two battling pieces play an ordinary game of chess; however, at each recursion depth d = 0…30, no subgame is played for the first d capturing moves. In the base game d = 0, so for every capturing move a subgame is played. If the depth equals 30, no subgames are played, as chess has a maximum of 30 captures.
In terms of penalties, the following seems most natural to me. Suppose a white piece is battling a black piece. If White wins the subgame, White captures the piece as usual. If the subgame is drawn, White has to choose another move. (If no other moves are possible, the game ends in stalemate.) Finally, if Black wins, White loses a tempo and it’s Black’s turn (which is often quite unfavorable for White!).
I like this angle. Another idea might be simply to limit the number of captures in the subgame, which would make a wellfounded recursion. For example, we could say that the attacker is allowed strictly fewer captures in the subgame as in the main game. That would make capturing difficult in the beginning, since you’d have to win the subgame without any captures for it to succeed. So perhaps a better idea would be: at depth d, allow 30-d captures for the attacker. In the beginning, this would be essentially like ordinary chess, but as the depth progressed, it would get harder and harder to succeed. This would in effect encourage play not requiring captures.
What about exploring a change in pieces’ perspectives?
Both the first description of the state of things (“[…] in order for a capture to occur successfully on the board, […] the two pieces would themselves sit down for their own game […]”) and the illustration (let’s not underestimate the role of images in creating a universe!) gave me the initial idea that it would be the two relevant pieces themselves playing the subgame – and not the human players playing the subgame on behalf of their pieces.
This means we have to postulate something about what the pieces know. My implicit and spontaneous assumption is that pieces don’t have a strategic view of the situation at any level higher than their own level – i.e. each piece always plays its own subgame with the goal of winning, because it is not aware that losing the subgame might be a good option from the perspective of the higher-level game.
This results in the fact that pieces will never play to lose, which makes the ‘Failed-capture’ option in the ‘Naïve recursion’ scenario more acceptable (and perhaps would be preventing strategic bad-playing even for other options – e.g. I don’t see why strategic bad-playing could not otherwise occur in the ‘Failed-capture-with-penalty’ option too).
There remains something else to be postulated: while we excluded upwards strategic knowledge (pieces don’t have, and thus don’t strategically use in their own subgame, knowledge of the situation at higher boards), this doesn’t tell if pieces know what the drawn-subgame rule is – and, if yes, if they use this knowledge strategically.
This means that, although it was just stated that pieces don’t play to lose, there is now a new question: do they always play to win? (this is without prejudice to the ability of a piece to go for a draw based solely on the internal circumstances of its own subgame).
Ultimately, given the premises, I think it feels natural to say that pieces always play to achieve the best result possible in their subgame: victory > draw > defeat.
I’m not even sure if and how these considerations propagate through the rest of the system, and it was not my ambition to explore it all. Just wanted to leave a seed!
Hello Joel David,
thank you for this wonderful idea!
A small detail: zugzwang is better than zugswang.
Best,
É.
Thanks, this is now fixed.
Like in Zeno’s paradox of Achilles and the tortoise, one could
for instance give only half the time of the previous layer to
a sub-game, so that the infinite tower sums up to a finite total
time. Either smaller pieces could play faster and faster (which
is no more unreasonable than the initial recursive idea ;-), or
they would be as slow as in the biggest game and Black would
eventually always lose on time. In either case, this seems to
be a natural way to define a well-founded recursion, doesn’t it?
I think the battling pieces should be egoistic: in a normal game of chess, the players try to protect their respective kings because they _are_ the kings. The battling pieces in a sub-game should however not care about loosing their kings but try to protect themselves (and a capture should be successful if the attacking piece can capture the attacked piece in the sub-game without being captured first, while kings can be lost without any effect). To make this non-trivial, the starting position of the sub-game would be one turn before the current turn of the super-game, with the attacked piece allowed to move. Not sure, however, if one needs some additional rules to prevent infinite recursion…
What an extremely interesting idea! It would lead to a radical change in game play, since we’d have temporarily to think of a particular pawn or bishop as proto king. But I think this would actually be quite interesting to do.
A little change in the game play which prevents infinite recursion: So, the main game is played by the kings, which is the reason they must not die. Assume a capture is attended, and for simplicity assume white tries to capture a piece of black. Then, a sub-game played by the two involved pieces is started given that the black piece (the one which should be captured and thus would “die”) is yet not already playing a game further up the recursion (see below why this makes sense). This sub-game starts one turn before the current state of its super-game, i.e. the last move of black is reset) and has the same rules as the main game, except that the sub-game is lost if the respective playing piece is lost OR if any piece playing a super-game is lost. In other words, the playing pieces become _additional_ “proto-kings”. Obviously, the recursion is finite since, at one point, every piece is a proto-king and thus no sub-game can be started anymore.
It makes sense that a sub-game is only started if the piece which should be captured is not yet a proto-king because, in the current super-game, the player already tries to protect this piece at all cost.
If the white capturing piece wins the sub-game, the capture is successfull and the super-game continues normally. If the black piece which should be captured wins the sub-game, or if there is a draw, the last turn of black in the super-game is reset (i.e. the super-game is set to the start-position of the sub-game). However, the black player is not allowed to make the same move in this turn again. As always, if a player cannot make a valid move anymore, he looses the game.
The underlying idea is very simple: The piece which should be captured forsees that it would be captured and “vetoes” the last move of the super-game given that it can prove (by playing the sub-game) that there is the possibility to at least achieve a draw in the super-game without itself being captured. Conversely, a piece only accepts a move after which it is captured if it is anyway captured under all possible moves or if the super-game would be lost otherwise.
Very interesting!
OK, my (hopefully) final idea: Every game is played by two pieces. The main game is played by the two kings. In the main game, the two kings are thus marked as “essential”. In the main game and all recursive games, essential means that the current player looses if he looses an essential piece. At the beginning of each turn, the player announces to its fellow pieces if its current goal is to win the game (goal=win), or if a draw would be sufficient (goal=win or draw). He then also announces its next move. The fellow pieces however can predict the close future (=the very next move of the opponent). In practice, this is done by making the move and letting the opponent player pre-commit to its move (eventually involving a set of additional recursive games, see below). If a piece would be captured in this next move of the opponent (and is not already marked as essential, reasoning see below), it can try to convince its player of an alternative strategy (=next move). It would only try to do so if it wouldn’t be captured (in the next or any further turn) with this strategy. Its player would only accept this new alternative strategy if the piece can convince him*her that he*she can achieve his*her goal with this strategy (win or win/draw). To prove that its strategy can achieve both goals, the piece starts a sub-game initialized at the current state with the piece which would capture it. The sub-game is identical to the current game, except that now also the piece which would be captured is marked as essential (additionally to all the other pieces already marked as essential; the piece of the opponent against which it plays is _not_ marked as essential). Note that, since the current players already try to protect their essential pieces at all cost, there is no point for an essential piece which would be captured to try to convince its player that it shouldn’t be captured. Once a player is convinced of an alternative strategy, his originally intended next move is forbidden (needed to prevent death-locks). It is easy to see that the depth of the resulting recursion is finite, since, (i) at worst, all pieces in the game get marked as essential and then no new game can thus be started; and (ii) each starting of a sub-recursion either leads to the original strategy beeing carried out (if the sub-game is lost) or to an additional forbidden move (if the sub-game is won).
It seems to me that this version of recursive chess should result in some meaningful game. Furthermore, it should have the property that the main game alone should look, for observers not aware of the recursive sub-games, like a valid classical game of chess which is played reasonably by the two players. It also seems that it might be possible to prove something along the line that the corresponding classical game can only be won (given a state) if the recursive one can be won, or vice versa. However, there is some non-trivial sequence dependency (there might be two valid next moves for which each a piece would be captured next, and for each of which the to be captured piece might be able to prove that the other one should be taken).
Here’s my idea: The initial game is played as normal, but then, when a capture would take place, the two pieces involved in the capture sit down to play a game of chess. As they are too busy playing chess, they are missing from their game of chess. This game then has the same rules as the layer above, until we get down to a win or two kings, which is an automatic draw. If there’s a draw, both pieces are removed from that layer of the game. Otherwise the losing piece is removed. Gameplay continues like this until someone gets checkmated at the very top layer, and then that player wins.
I meant that player loses.