A few months ago, Peter Doyle sent me a cryptic email, containing only the following photo and a subject line containing the title of this post.
I was mystified, until François Dorais subsequently explained that he had given a short presentation on recent progress in foundations for prospective graduate students at Dartmouth.
I’m glad to know that the upcoming generation will have an accurate historical perspective on these things! 🙂
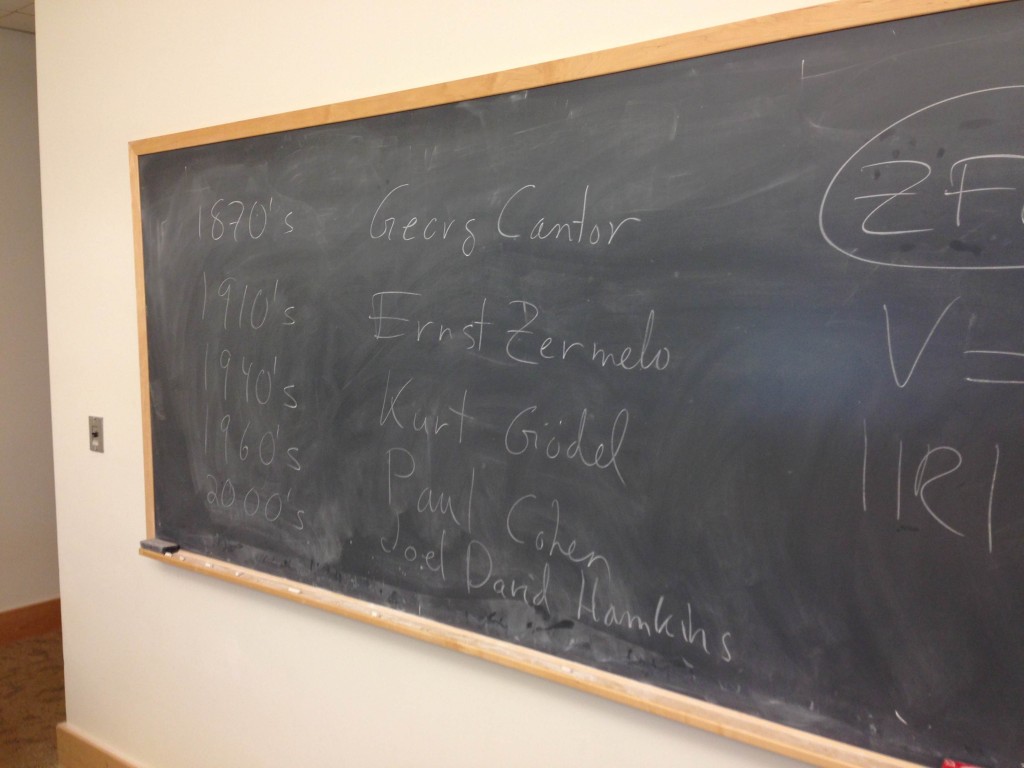
Hahaha! The prospective graduate students really enjoyed learning about the multiverse and they were mystified by the idea that finiteness wasn’t as absolute as they thought it was.
Speaking of that, have I told you about the theorem I recently proved with Ruizhi Yang? There are models of set theory $M_1$ and $M_2$ that agree on what they think is the standard model of arithmetic $\mathbb{N}^{M_1}=\mathbb{N}^{M_2}$, yet they have an arithmetic sentence $\sigma$ such that $M_1$ thinks $\sigma$ is true and $M_2$ thinks $\neg\sigma$. We’ll be posting the paper soon.