 Let me show you how to hand-draw an image of a chessboard in perspective, using only a straightedge. There is no need to measure any distances or to make calculations of any kind. All you need is a straightedge, paper and your pen or pencil.
Let me show you how to hand-draw an image of a chessboard in perspective, using only a straightedge. There is no need to measure any distances or to make calculations of any kind. All you need is a straightedge, paper and your pen or pencil.
Imagine the vast doodling potential! A person who happens to be stuck in a lecture on some other less interesting topic could easily make one or more elaborate chessboards in perfect perspective, using only a straightedge! Please carry out the construction and then share your resulting images. I would love to see them.
To begin, give yourself a horizon at the top of the page, with two points at infinity (in orange), and also two points (blue) that will become the front and back corner of your chessboard. You can play around with different arrangements of these points, which will lead ultimately to different perspective views.
Using your straightedge, draw the lines from those reference points to the points at infinity. The resulting enclosed region will ultimately become the main chess board. One can alternatively think of starting with the front edges of the desired board, and then setting a horizon and using that to determine the points at infinity, and then adding the back edges.  If you like, you can add a third point at infinity down below, and a front bottom reference point (blue), to give the board some thickness. Construct the lines to the bottom point at infinity.
If you like, you can add a third point at infinity down below, and a front bottom reference point (blue), to give the board some thickness. Construct the lines to the bottom point at infinity.
The result is now the main outline of your chessboard as a rectangular solid.
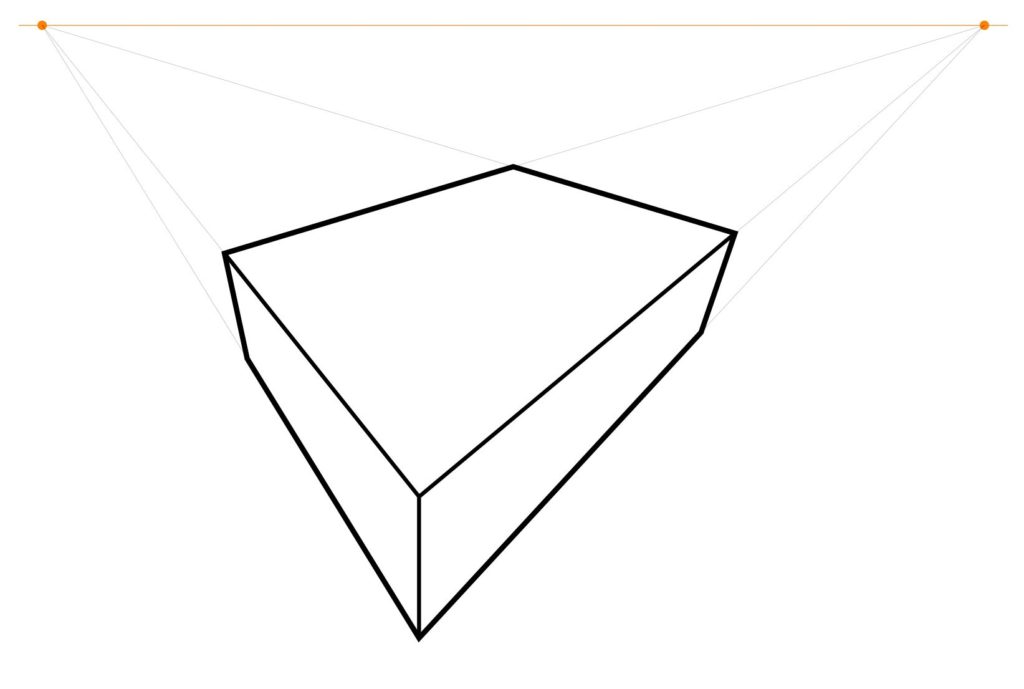 Next, construct the center point of the top face, by drawing the two diagonals and finding the intersection point. I call this the center point, because it is the point that represents in the perspective view the actual center point of the chessboard, even though this point is not in the “center” of the quadrilateral representing the board. It is remarkable that one can find that point without needing to measure or calculate anything, simply because the two straight lines of the diagonal of the chessboard intersect at that point, and this remains true in the perspective view. This is the key idea that enables the entire construction method to proceed with only a straightedge.
Next, construct the center point of the top face, by drawing the two diagonals and finding the intersection point. I call this the center point, because it is the point that represents in the perspective view the actual center point of the chessboard, even though this point is not in the “center” of the quadrilateral representing the board. It is remarkable that one can find that point without needing to measure or calculate anything, simply because the two straight lines of the diagonal of the chessboard intersect at that point, and this remains true in the perspective view. This is the key idea that enables the entire construction method to proceed with only a straightedge.
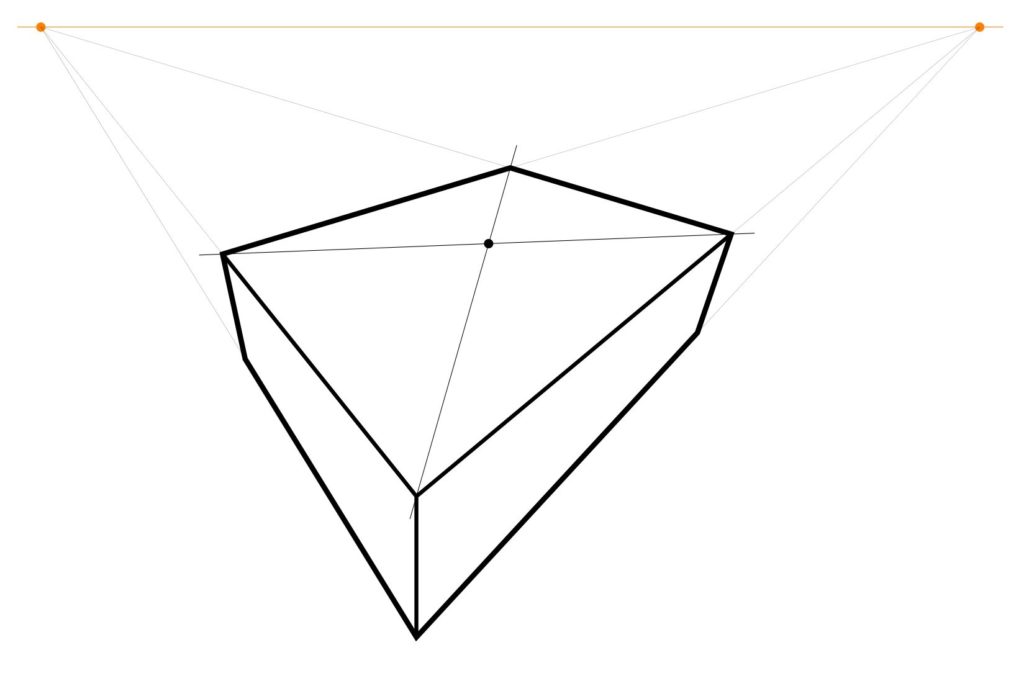 Construct the midpoint lines by drawing the lines from that centerpoint to the points at infinity.
Construct the midpoint lines by drawing the lines from that centerpoint to the points at infinity.
 Now you have the chessboard with the main midlines drawn.
Now you have the chessboard with the main midlines drawn.
 Construct the center points of the two diagonal squares, by intersecting the diagonals of each of them.
Construct the center points of the two diagonal squares, by intersecting the diagonals of each of them.
 Construct the lines that extend those points to the points at infinity.
Construct the lines that extend those points to the points at infinity.
 Thus, you have constructed the main 4 x 4 grid.
Thus, you have constructed the main 4 x 4 grid.
 You can extend the grid lines down to the bottom point at infinity like so:
You can extend the grid lines down to the bottom point at infinity like so:
 One can stop with the 4 x 4 board, if desired. Simply add suitable shading, and you’ve completed the 4 x 4 chessboard in perspective.
One can stop with the 4 x 4 board, if desired. Simply add suitable shading, and you’ve completed the 4 x 4 chessboard in perspective.
 Alternatively, one can continue with one more iteration to construct the 8 x 8 board. From the 4 x 4 grid (with no shading yet) simply construct the center points of the squares on the main diagonal, and extend those lines to infinity. This will enable you to draw the 8 x 8 grid lines, and after shading, you’ll have the complete chessboard.
Alternatively, one can continue with one more iteration to construct the 8 x 8 board. From the 4 x 4 grid (with no shading yet) simply construct the center points of the squares on the main diagonal, and extend those lines to infinity. This will enable you to draw the 8 x 8 grid lines, and after shading, you’ll have the complete chessboard.
The initial arrangement of points affects the nature of the perspective view. Having the points at infinity very far away will produce something closer to orthoprojection; having them close produces a more extreme perspective, which simulates a view from a vantage point extremely close to the board.
Please give the construction a try! All you need is paper, pencil and a straightedge! Provide links below in the comments to photos of your creations.
Meanwhile, let me point you towards my follow post, How to draw infinite chessboards by hand in perfect perspective, using only a straightedge. The difference between the methods is that the method of this post is about subdividing a given board, and the other method is about generating arbitrarily large chessboards from a given unit square.
I learned these construction method years ago from my CUNY geometer colleague Ilya Kofman.




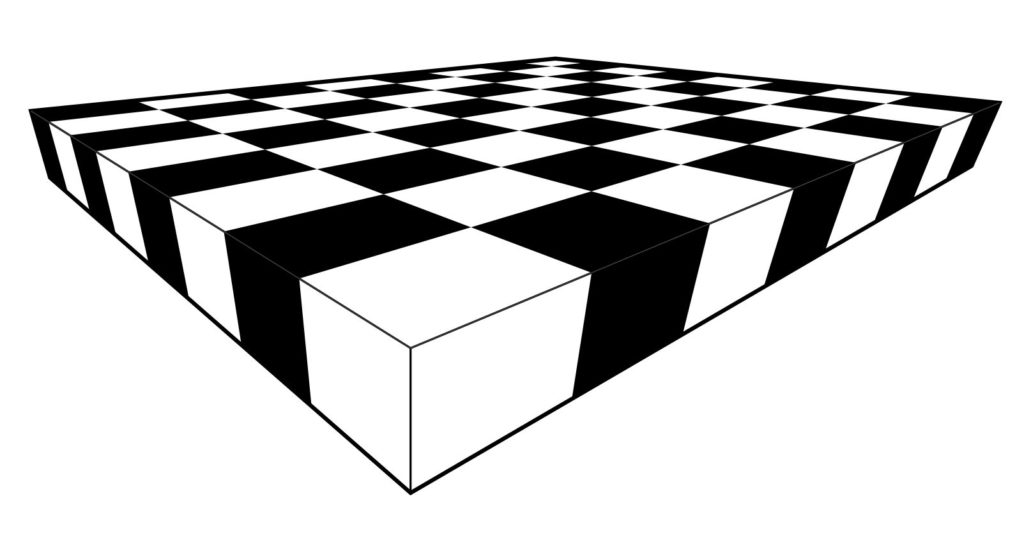



Pictures of hand-drawn chessboards available here: https://twitter.com/JDHamkins/status/1034931439777837058?s=19.
haha. awesome!
Here is a different way of starting, which may lead to better results. Start with the horizon and two points at infinity, plus the front vertex. Extend that vertex to each point at infinity. Now, pick a line roughly parallel to the horizon, which will become the main horizontal diagonal of the chessboard. This line determines the left and right corners of the chessboard, which when extended to the points at infinity, will determine the back corner, and one proceeds as before. By picking the line parallel to the horizon, one is ensuring in effect (because chessboards are square) that the board is level with respect to the horizon, and this is the expected case, which will make a more pleasant image.
But actually, now I have become a little confused about this. Can some geometer help me out? Is my original front/back vertex approach fully correct, in that the resulting perspective could in fact be the perspective view of an actual square chessboard? If you pick the back vertex too far to one side, it often ends up looking strangely rectangular. And what is the importance of having the main horizontal diagonal parallel to the horizon?
Actually, I don’t think it is possible to construct a parallel to a given line through a given point, using only straightedge. Is this right? (Please comment if you have proof.) If so, then one couldn’t perfectly carry out the alternative construction, although obviously one could approximate it.
Projective plane geometry is defined using only types “point”, “line”, a relation “point p lies on line L”, and a few axioms:
https://en.wikipedia.org/wiki/Projective_geometry#Whitehead's_axioms
The real projective plane is a model which I believe corresponds to what you can do with just a straightedge – well, on a piece of paper that has points at infinity. This model has a symmetry group, the projective group PSL(3,R), which is strictly larger than the group of affine transformations of the plane. The affine transformations preserve the usual concept of ‘parallel lines’ (which in projective geometry are lines that only meet at infinity). The rest of the transformations carry parallel lines to non-parallel lines. Because these other transformations are symmetries of this model, the concept of ‘parallel lines’ can’t be definable in projective geometry. I believe this implies you can’t construct a parallel to a given line through a given point using only a straightedge.
The soft spots in this argument are marked with “I believe”. Someone should have studied whether what you can construct with a straightedge is exactly what you can define in projective geometry. Probably in the 1800s or early 1900s!
Now that I think about it, it should be easy to see that what’s constructible using a straight-edge is what’s definable in axiomatic projective plane geometry if we use these axioms:
(P1) Any two distinct points lie on a unique line.
(P2) Any two distinct lines meet in a unique point.
(P3) There exist at least four points of which no three are collinear.
and we assume that even points at infinity are constructible using a straight-edge.
The last axiom, by the way, serve to eliminate a well-understood class of models that people consider annoying. In the presence of the other axioms it’s equivalent to “there exist at least four lines of which no three intersect in a common point.” So the axioms are self-dual.
You may have thought you were getting away from axioms, model theory etc., but you’re not!
Thanks so much for these comments!
Really nice! I’m making mine now. So cool that you can divide equal portions in perspective! I think it works best, as you say above, to make the horizon line first, then the 3 dots for the foremost corners, and then find your infinity points by connecting to the horizon line so that you can fit it on your drawing paper. I got stuck the first time.
See my follow up post about an alternative way to proceed, which makes it easy to construct very large boards, whose size needn’t be fixed in advance. http://jdh.hamkins.org/draw-an-infinite-chessboard-in-perspective/
Pingback: Draw an infinite chessboard in perspective, using straightedge only | Joel David Hamkins