My student Corey Switzer has just completed a paper:
Corey Switzer, The Cichoń Diagram for Degrees of Relative Constructibility, ArXiv e-print:1801.06497.
Abstract. Following a line of research initiated in Brendle/Brooke-Taylor/Ng/Nies, I describe a general framework for turning reduction concepts of relative computability into diagrams forming an analogy with the Cichoń diagram for cardinal characteristics of the continuum. I show that working from relatively modest assumptions about a notion of reduction, one can construct a robust version of such a diagram. As an application, I define and investigate the Cichoń Diagram for degrees of constructibility relative to a fixed inner model W. Many analogies hold with the classical theory as well as some surprising differences. Along the way I introduce a new axiom stating, roughly, that the constructibility diagram is as complex as possible.
This interesting paper concerns a generalization of the Cichoń diagram to arbitrary reducibility notions, focussing on the case of the constructibility degrees, or somewhat more generally, relative constructibility
The classes are defined by an abstract generalization of the ideas underlying the familiar cardinal characteristics and the classical Cichoń diagram. Namely,
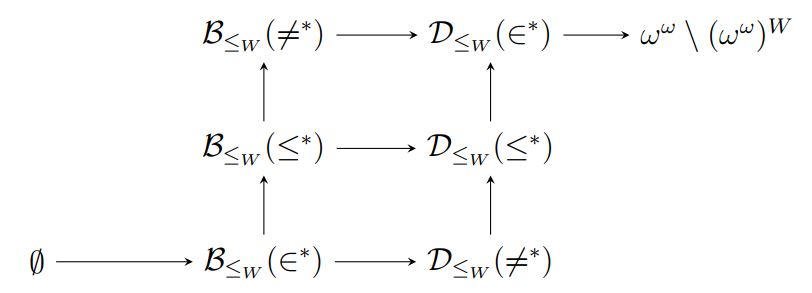 These classes fit together in a way that forms a robust analogy with the classical Cichoń diagram.
These classes fit together in a way that forms a robust analogy with the classical Cichoń diagram.
In his paper, Corey proves that the diagram is complete with respect to the inclusions indicated, by analyzing the nature of the diagram in various forcing extensions of
In the end, he shows that in a suitable (proper) forcing extension, one can achieve all the separations simultaneously.
 Indeed, the assertion that all separations are attained can be taken as a set-theoretic principle or axiom of its own, the complete Cichoń diagram assertion CD. He proves, for example, that CD is a consequence of the maximality principle.
Indeed, the assertion that all separations are attained can be taken as a set-theoretic principle or axiom of its own, the complete Cichoń diagram assertion CD. He proves, for example, that CD is a consequence of the maximality principle.






Pingback: The Cichon Diagram for Degrees of Relative Constructibility – Corey Bacal Switzer