I had the pleasure a few weeks ago to visit my daughter’s math class at her school and undertake some fun math activities with the sixth graders (11-12 years old, all girls). What a fun time we had!
The topic was orthoprojection and the problem of gaining insight about a three-dimensional object or arrangement by considering its various orthogonal projections.
I had prepared a collection of puzzles, which I hoped would challenge the students in spatial reasoning and abstract visualization. (The puzzle booklet is available at bottom.)
The puzzles involved orthogonal projections of arrangements of unit blocks.
Unit blocks are a certain kind of wooden block toy, which exhibit precise dimensions in the ratio
Unit blocks are commonly found in American elementary schools and kindergartens, and woodworkers will recognize that one can make a set of unit blocks from standard
For the school visit, I brought sufficient blocks for all the girls, and explained that we were going to play with blocks the way that a mathematician or engineer might play with blocks. And I had prepared a puzzle booklets, one per child (available below).
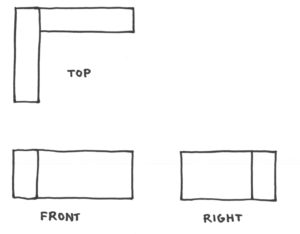
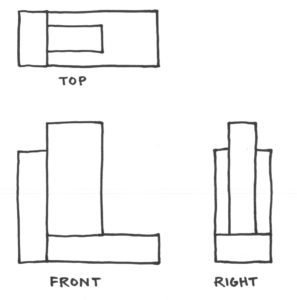
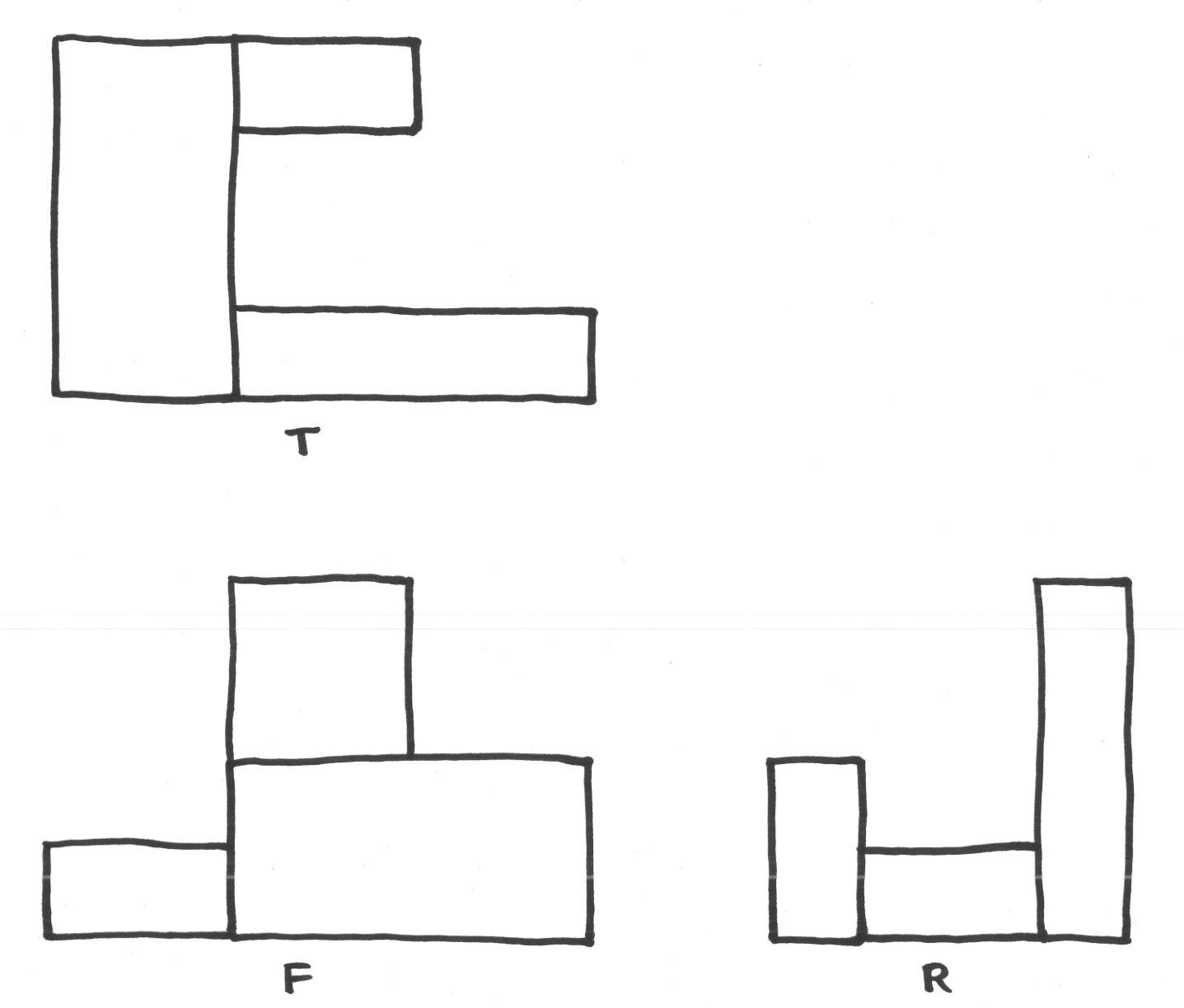
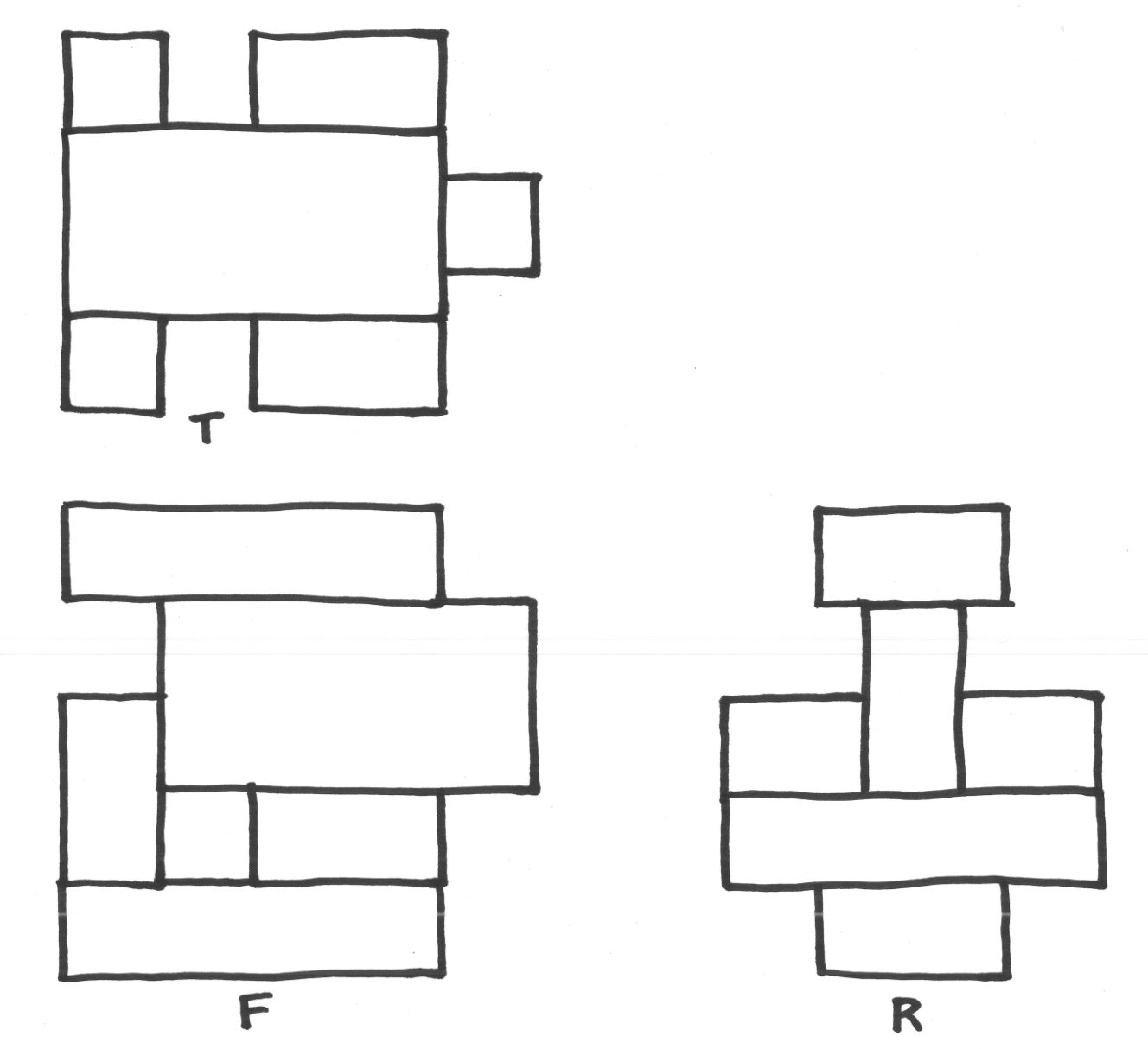
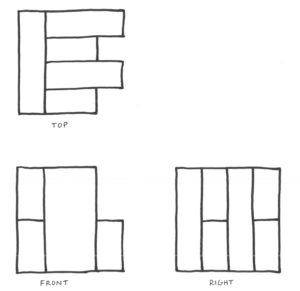
For each puzzle, one sees the front view, top view and right side view of an arrangement of blocks, and the challenge is to assemble the blocks so as to realize those views. (In these puzzles, I had chosen not to show any hidden lines and edges, to make them slightly more challenging, although it would also make sense to me to show hidden lines; it would be customary to do so with a dashed line.)

 Here are a few more easy examples with solutions.
Here are a few more easy examples with solutions.
It happens that these front/top/side projection view problems inspire some deep feelings in me, for they remind me of my father, who was a mechanical engineer. In my childhood, he would often bring home and show me blueprints of the machines or machine parts that he was designing or working with, and those blueprints were filled with front/top/side projection views of the various parts. In pre-computer design days, engineers would specify their machine parts by providing the various othogonal views. (Nowadays, of course, computers are used and one can compute orthogonal and perspective views from any angle.)
In my daughter’s classroom, the students took up the puzzles with a seriousness that shocked me. Once we had passed out the puzzle booklets and distributed the blocks, the girls just steamed through the puzzles, one after the other, totally absorbed. They didn’t want any hints or advice or help of any kind; they just went from each puzzle to the next, solving them one after another. There were a sufficient number of blocks for them all to work on the smaller puzzles on their own, but for the larger puzzles, they formed groups and combined blocks. It was a big success!
Without further ado, here are your puzzles. I’ve also included some photos below, out of order, and some puzzles do not match a photo and vice versa, but you can look at the photos if you need a hint.
After these puzzles, we moved on to the inverse problem. The girls made their own arrangement of blocks and then drew all six orthogonal projections: front, top, right, left, back, bottom. You can draw them on the net of a cube, so that you can imagine folding the cube so as to realize the projections.
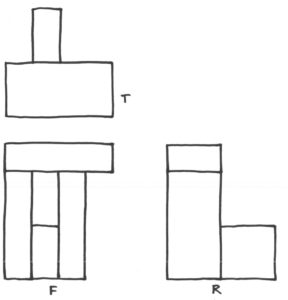
And after this, we moved beyond unit blocks to more general shapes. Can you solve the following projection puzzles?
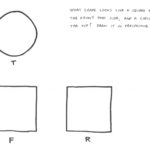
The most challenging puzzle was the following. Can you imagine a solid that appears as a square from the front, a circle from the top and a triangle from the right side?
The complete puzzle booklet is available here: Fun with orthoprojections!
(And here is an alternative version of the puzzles made by David Butler for use with Jenga blocks, which have the dimensional ratios
Although I made the puzzles with six-graders in mind, the puzzles are interesting for people of any age, and I have proof: a picture of some of my CUNY math-major college students solving the puzzles in my office.
And here are videos of some fascinating sculptures playing with orthoprojections:
https://youtu.be/pn74pSlznj8

























Instead of doing just math-for-kids posts, you should make a math-for-cats post where you discuss the physics of falling cats and how cats are able to miraculously land on their feet when you drop them upside down without violating the law of conservation of angular momentum.
Smarter Every Day already covered that:
Thank you so much! This is so funny! I don’t have blocks at home, so I draw everything in perspective (with good old pen and paper). I think I’m also going to try this with OpenSCAD ( cube([1,2,4], 0, 0) )…