I’d like to discuss the issue of error and error propagation in the constructions of classical geometry. How does error propagate in these constructions? How sensitive are the familiar classical constructions to small errors in the use of the straightedge or compass?

Let me illustrate what I have in mind by considering the classical construction of Apollonius of the perpendicular bisector of a line segment $AB$.  One forms two circles, centered at $A$ and $B$ respectively, each with radius $AB$. These arcs intersect at points $P$ and $Q$, respectively, which form the perpendicular bisector, meeting the original segment at the midpoint $C$.

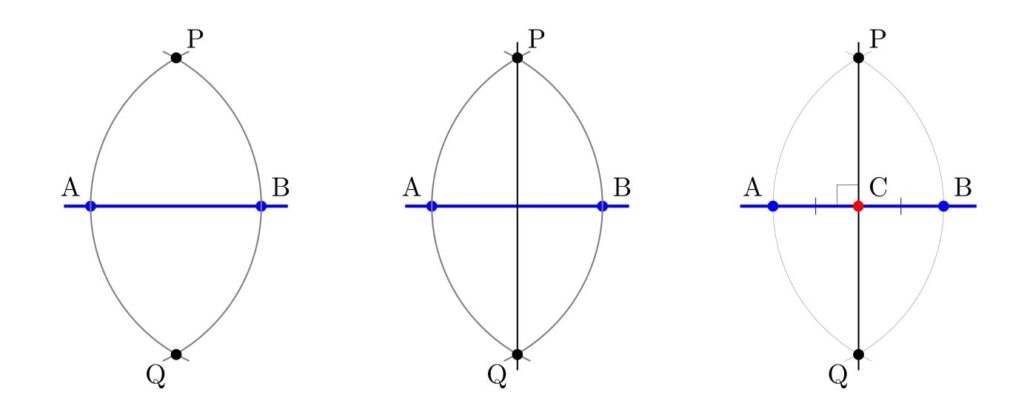
That is all fine and good, and one can easily prove that indeed $PQ$ is perpendicular to $AB$ and that $C$ is the midpoint of $AB$, as desired.

When carrying out such a construction in practice, however, there will inevitably be some small errors. We do not expect to implement it exactly, with infinite precision, but rather, we expect some small errors in the placement of the compass or straightedge, and perhaps these errors may accumulate and they propagate through the construction. What I would like to discuss is the sensitivity of this construction and the other classical constructions to these small errors.

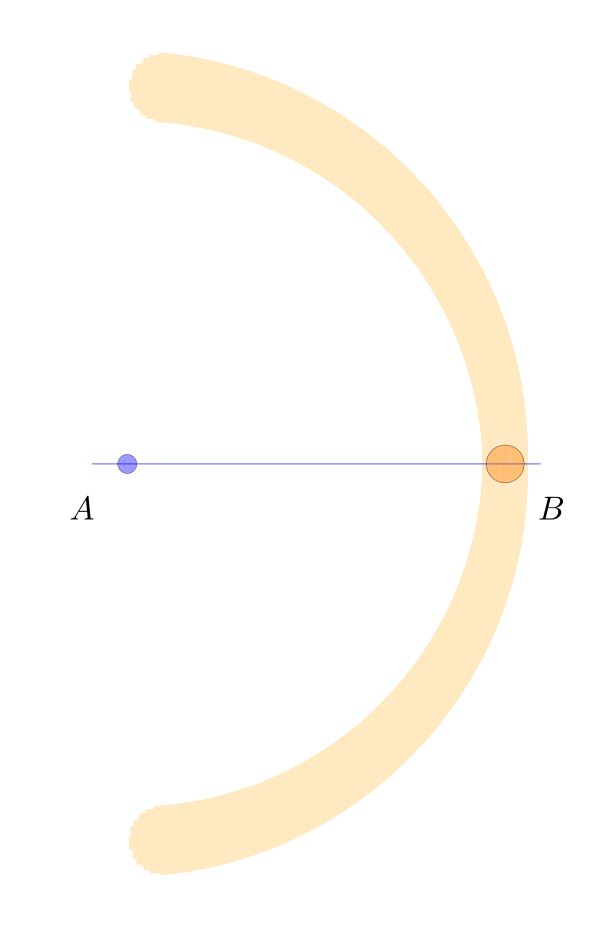
For example, suppose that we are given points $A$ and $B$. When we seek to construct the circle centered at $A$ with radius $AB$, we place the point of the compass at $A$, and this placement may have some small error deviating from $A$, landing somewhere in the blue circle. Similarly, the writing (or etching) implement end of the compass is placed at $B$, with its own possibly different error, landing the orange circle at $B$. The arc actually resulting will be some arc arising with some such small errors, like this:

We may represent the space of all arcs that could arise in conformance with those error bounds as the blurred orange arc below. This image was created simply by drawing many dozens of such arcs in orange, with various choices for the center and radius within the error circles, and blending the results together.

We carry out the same construction with similar errors for the other arc, centered at $B$ and passing through $A$. These arcs overlap in the darker orange regions above and below, determining the points $P$ and $Q$.

The actual arcs we draw and the corresponding vertical will land somewhere inside these blurred regions, perhaps like this:

Note that in this particular case, the resulting line $PQ$ is noticably non-perpendicular to $AB$, and the resulting point $C$ is noticably not the midpoint. Consider the space of all the bisectors $PQ$ that might arise in conformance with our errors on $A$ and $B$, showing the result as the vertical red shaded region.   The darker red region is the space of possible points $C$ that we might have constructed as the “midpoint” $C$, in conformance with the error estimates.

Given the size of the original error bounds on the points $A$ and $B$, it may be surprising that even such a standard simple construction as this — constructing the perpendicular bisector and midpoint of a segment — appears to have comparatively large error propagation, since the shaded red region $C$ is quite large and includes many points that one would not say are close to being the midpoint.  In this sense, the Apollonius perpendicular bisector construction appears to be sensitive to the errors of compass placement.

Is there a better construction? For example, in terms of improving the accuracy at least of the perpendicularity of $PQ$ to $AB$, it would seem to help to use a much larger circle, which would lower the variation in the resulting “right” angle.  But this is partly because we have so far assumed that compass error arises only with the placement of the points of the compass, and not during the course of actually drawing the arc. But of course, one can imagine that errors arise from a flexing of the compass during use, causing it to deviate from circularity, or from slippage, which might reasonably be expected to cause increasing error with the length or degree of the arc, and so on, and such a model of error might have greater errors with large circles.

One could in principle carry out similar analyses for any geometric construction, and use the corresponding results to compare the sensitivity of various methods for constructing the same object, as well as modeling different sources of error.  The goal might be to mount a precise analysis of all the standard constructions and compare competing constructions for accuracy.

There is a literature of papers doing precisely this, and I will try to post some references later (or please do so in the comments, if you have some good ones).

Another approach to error estimation would be to think of the errors at points $A$ and $B$ as probability distributions, centered at $A$ and $B$ and with a certain variation; and one then gets corresponding distributions for the points $P$ and $Q$, which are not rigid shapes as in my diagrams, but qualitatively similar distributions spread out in that region, and a resulting probability distribution for the point $C$.

Finally, let me mention that one might hope to improve the accuracy of a construction, simply by repeating it and averaging the result, or by some other convergence algorithm. For example, as a first step, we might simply perform the Apollonius bisector construction twice, producing midpoint candidates $C_0$ and $C_1$, and we could proceed simply find the midpoint of $C_0C_1$ as a further presumably more accurate midpoint. Or we could iterate in some other manner and hope to converge to the actual midpoint. For example, we could produce seven midpoint candidates, and take the resulting median point.