This will be a talk for the Workshop on Logic, Rationality, and Intelligent Interaction at the CSLI, Stanford University, May 27-28, 2016.

Abstract. To what extent does a structure determine its theory of truth? I shall discuss several surprising mathematical results illustrating senses in which it does not, for the satisfaction relation of first-order logic is less absolute than one might have expected. Two models of set theory, for example, can have exactly the same natural numbers and the same arithmetic structure 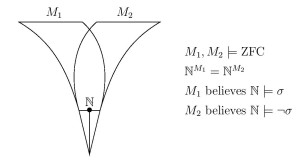$⟨\mathbb{N},+,\cdot ,0,1,<⟩$, yet disagree on what is true in this structure; they have the same arithmetic, but different theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $⟨V_{\delta },\in ⟩$ in common, yet disagree about whether it is a model of ZFC. These theorems and others can be proved with elementary classical model-theoretic methods, which I shall explain. On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.

Slides | Main article: Satisfaction is not absolute | CLSI 2016 | Abstract at CLSI