This was an online talk 15 April 12:15 for the CUNY Set Theory Seminar. Held on Zoom at 876 9680 2366.

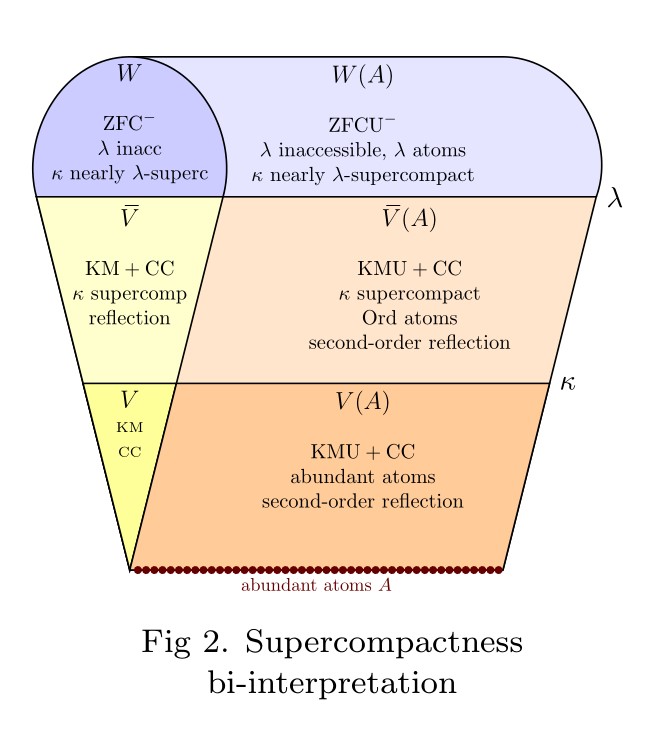
Abstract. I shall give a general introduction to urelement set theory and the role of the second-order reflection principle in second-order urelement set theory GBCU and KMU. With the abundant atom axiom, asserting that the class of urelements greatly exceeds the class of pure sets, the second-order reflection principle implies the existence of a supercompact cardinal in an interpreted model of ZFC. The proof uses a reflection characterization of supercompactness: a cardinal
See the article at: Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal



Unfortunately I can’t make this, but it looks super interesting. Question:
1. Can I see slides/paper?
2. Have you considered how this will relate to Chris Menzel’s theories of `wide sets’?
Paper is currently still in progress (frantically still writing!), but should be available before too long. I don’t know much about Menzel’s theory, but I’ll look into it. Sounds superficially like it could be related, since a fundamental feature of the abundant atom axiom is that the universe is very wide in comparison with its height.
Update: paper is now available at: http://jdh.hamkins.org/second-order-reflection-with-abundant-urelements/
Seconding Neil’s second question (hehe), there seems to be some interest in the modal set theory and metaphysics circles in the following principle: for each cardinal
Hi Jason! I’m so glad you’re also aware of this potential connection between our work and modal metaphysics! Two quick comments:
(1) The abundant atom axiom will go far beyond the principle you mentioned (plz come to the talk for its formal definition 🙂 )
(2) The recombination paradoxes in Uzquiano’s paper appeal to the limitation of size principle (LS). But LS is a very special second-order choice principle in KMU: it doesn’t follow from the second-order choice principle (RP_2) assuming large cardinals. And what is really surprising is the exact strength of KMU + RP_2 + ~LS….
Pingback: Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal | Joel David Hamkins