This was an online talk 15 April 12:15 for the CUNY Set Theory Seminar. Held on Zoom at 876 9680 2366.

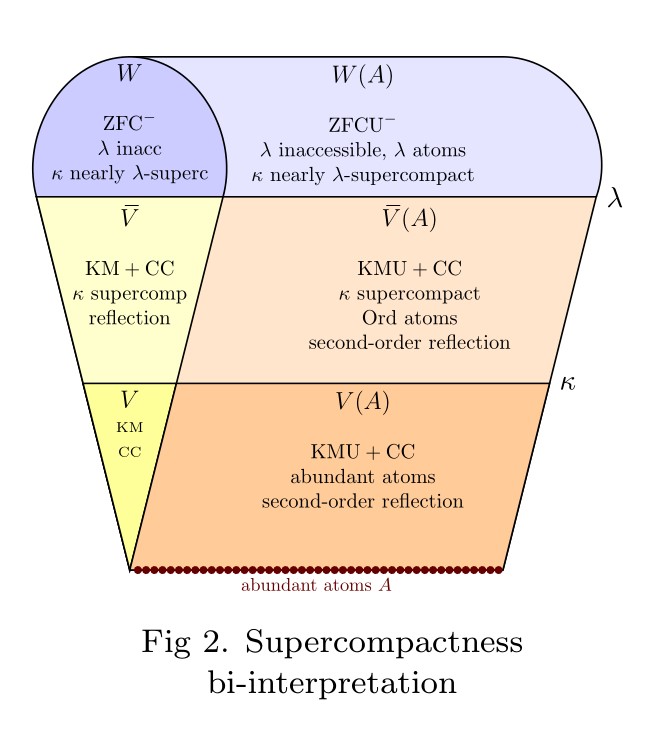
Abstract. I shall give a general introduction to urelement set theory and the role of the second-order reflection principle in second-order urelement set theory GBCU and KMU. With the abundant atom axiom, asserting that the class of urelements greatly exceeds the class of pure sets, the second-order reflection principle implies the existence of a supercompact cardinal in an interpreted model of ZFC. The proof uses a reflection characterization of supercompactness: a cardinal $\kappa$ is supercompact if and only if for every second-order sentence $\psi$ true in some structure $M$ (of any size) in a language of size less than $\kappa$ is also true in a first-order elementary substructure $m\prec M$ of size less than $\kappa$. This is joint work with Bokai Yao.

See the article at: Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal