As a guest today in my daughter’s second-grade classroom, full of math-enthusiastic seven-and-eight-year-old girls, I led a mathematical investigation of graph coloring, chromatic numbers, map coloring and Eulerian paths and circuits. I brought in a pile of sample graphs I had prepared, and all the girls made up their own graphs and maps to challenge each other. By the end each child had compiled a mathematical “coloring book” containing the results of their explorations.  Let me tell you a little about what we did.

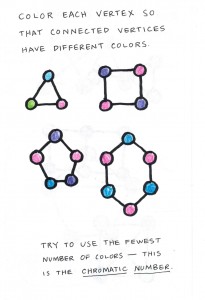
We began with vertex coloring, where one colors the vertices of a graph in such a way that adjacent vertices get different colors. We started with some easy examples, and then moved on to more complicated graphs, which they attacked.

The aim is to use the fewest number of colors, and the chromatic number of a graph is the smallest number of colors that suffice for a coloring.  The girls colored the graphs, and indicated the number of colors they used, and we talked as a group in several instances about why one needed to use that many colors.

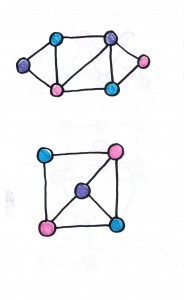
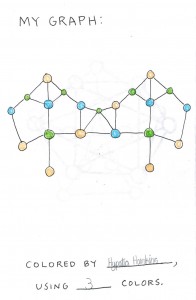
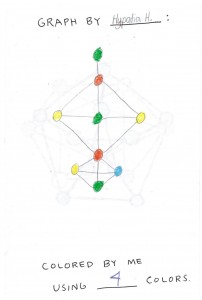
Next, the girls paired off, each making a challenge graph for her partner, who colored it, and vice versa.

Map coloring, where one colors the countries on a map in such a way that adjacent countries get different colors, is of course closely related to graph coloring.

The girls made their own maps to challenge each other, and then undertook to color those maps. We discussed the remarkable fact that four colors suffice to color any map. 

Next, we considered Eulerian paths and circuits, where one traces through all the edges of a graph without lifting one’s pencil and without retracing any edge more than once. We started off with some easy examples, but then considered more difficult cases. 

An Eulerian circuit starts and ends at the same vertex, but an Eulerian path can start and end at different vertices.

We discussed the fact that some graphs have no Eulerian path or circuit.  If there is a circuit, then every time you enter a vertex, you leave it on a fresh edge; and so there must be an even number of edges at each vertex.  With an Eulerian path, the starting and ending vertices (if distinct) will have odd degree, while all the other vertices will have even degree.

It is a remarkable fact that amongst connected finite graphs, those necessary conditions are also sufficient.  One can prove this by building up an Eulerian path or circuit (starting and ending at the two odd-degree nodes, if there are such);  every time one enters a new vertex, there will be an edge to leave on, and so one will not get stuck.  If some edges are missed, simply insert suitable detours to pick them up, and again it will all match up into a single path or circuit as desired.  (But we didn’t dwell much on this proof in the second-grade class.)

Meanwhile, this was an excellent opportunity to talk about The Seven Bridges of Königsberg.  Is it possible to tour the city, while crossing each bridge exactly once?

The final result: a booklet of fun graph problems!

The high point of the day occurred in the midst of our graph-coloring activity when one little girl came up to me and said, “I want to be a mathematician!”  What a delight!

Andrej Bauer has helped me to make available a kit of my original uncolored pages (see also post at Google+), if anyone should want to use them to make their own booklets.  Just print them out, copy double-sided (with correct orientation), and fold the pages to assemble into a booklet; a few staples can serve as a binding.

See also my followup question on MathOverflow, for the grown-ups, concerning the computational difficulty of producing hard-to-color maps and graphs.

Finally, check out my new book: