This morning I had the pleasure to be a mathematical guest in my daughter’s third-grade class, full of inquisitive eight- and nine-year-old girls, and we had a wonderful interaction. Following up on my visit last year (math for seven-year-olds), I wanted to explore with them some elementary ideas in graph theory, which I view as mathematically rich, yet accessible to children. 
My specific aim was for them to discover on their own the delightful surprise of the Euler characteristic for connected planar graphs.

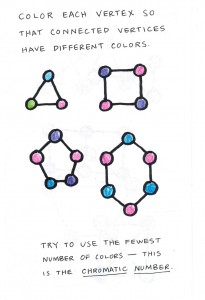
We began with a simple example, counting together the number of vertices, edges and regions. For counting the regions, I emphasized that we count the “outside” region as one of the regions.
Then, I injected a little mystery by mentioning that Euler had discovered something peculiar about calculating . Could they find out what it was that he had noticed?

Each student had her own booklet and calculated the Euler characteristic for various small graphs, as I moved about the room helping out.

Eventually, the girls noticed the peculiar thing — they kept getting the number two as the outcome! I heard them exclaim, why do we keep getting two? They had found Euler’s delightful surprise!

The teachers also were very curious about it, and one of them said to me in amazement, “I really want to know why we always get two!”

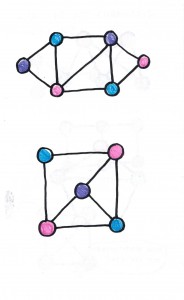
With the students, I suggested that we try a few somewhat more unusual cases, to see how robust the always-two situation really was. But in these cases, we still got two as the result.
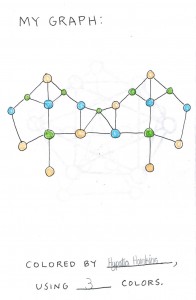
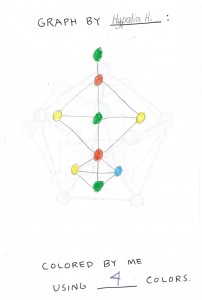
The girls made their own graphs and tested the hypothesis.

Eventually, of course, I managed to suggest some examples that do in fact test the always-two phenomenon, first by looking at disconnected graphs, and then by considering graphs drawn with crossing edges.

In this way, we were led to refine the hypothesis to the case of connected planar graphs.
Now, it was time for proof. I was initially unsure whether I should actually give a proof, since these were just third-graders, after all, and I thought it might be too difficult for the students. But when the teachers had expressed their desire to know why, they had specifically encouraged me to give the argument, saying that even if some students didn’t follow it, there was still value merely in seeing that one can mount an argument like that. Excellent teachers!
The idea of the proof is that is true at the start, in the case of a graph consisting of one vertex and no edges. Furthermore, it remains true when one adds one new vertex connected by one new edge, since the new vertex and new edge cancel out. Also, it remains true when one carves out a new region from part of an old region with the addition of a single new edge, since in this case there is one new edge and one new region, and these also balance each other. Since any connected planar graph can be built up in this way by gradually adding new vertices and edges, this argument shows for any connected planar graph. This is a proof by mathematical induction on the size of the graph.


Next, we moved on to consider some three-dimensional solids and their surfaces. With various polyhedra, and the girls were able to verify further instances of .


The girls then drew their own solids and calculated the Euler characteristic. I taught them how to draw a cube and several other solids pictured here; when the shape is more than just a simple cube, this can be a challenge for a child, but some of the children made some lovely solids:

In the end, each child had a nice little booklet to take home. The images above are taken from one of the students in the class.

What a great day!
You can find a kit of the booklet here:
See also the account of my previous visit: Math for seven-year-olds: graph coloring and Eulerian paths.