Let us explore the vast and densely populated expanses of the lattice of all sets of natural numbers—the power set lattice .
We find in this lattice every possible set of natural numbers , and we consider them with respect to the subset relation . This is a lattice order because the union of two sets is their least upper bound with respect to inclusion and the intersection is their greatest lower bound. Indeed, it is a distributive lattice in light of , but furthermore, as a power set algebra it is a Boolean algebra and every Boolean algebra is a distributive lattice.
The empty set is the global least element at the bottom of the lattice, of course, and the whole set is the greatest element, at the top. The singletons are atoms, one step up from , while their complements are coatoms, one step down from . One generally conceives of the finite sets as clustering near the Earthly bottom of the lattice, finitely close to , whereas the cofinite sets soar above, finitely close to the heavenly top. In the vast central regions between, in contrast, we find the infinite-coinfinite sets, including many deeply interesting sets such as the prime numbers, the squares, the square-free numbers, the composites, and uncountably many more.
Question. Which familiar orders can we find as suborders in the power set lattice of all sets of natural numbers?
We can easily find a copy of the natural-number order in the power set lattice , simply by considering the chain of initial segments:
This sequence climbs like a ladder up the left side of the main figure. Curious readers will notice that although every one of these sets is finite and hence conceived as clinging to Earth, as we had said, nevertheless there is no upper bound for this sequence in the lattice other than the global maximum —any particular natural number is eventually subsumed. Thus one climbs to the heavens on this ladder, which stretches to the very top of the lattice, while remaining close to Earth all the while on every rung.
The complements of those sets similarly form a infinite descending sequence:
This chain of cofinite sets dangles like a knotted rope from the heavens down the right side of the main figure. Every knot on this rope is a cofinite set, which we conceived as very near the top, and yet the rope dangles temptingly down to Earth, for there is no lower bound except .
Can we find a copy of the discrete integer order in the power set lattice?
Yes, we can. An example is already visible in the red chain at the right side of main lattice diagram, a sky crane hanging in space. Standing at the set of odd numbers, we can ascend in discrete steps by adding additional even numbers one at a time; or we can descend similarly by removing successive odd numbers. The result is a discrete chain isomorphic to the integer order , and it is unbounded except by the extreme points and .
Can we find a dense order, say, a copy of the rational line ?
What? You want to find a dense order in the lattice of sets of natural numbers? That might seem impossible, if one thinks of the lattice as having a fundamentally discrete nature. The nearest neighbors of any set, after all, are obtained by adding or removing exactly one element—doing so makes a discrete step up or down with no strictly intermediate set. Does the essentially discrete nature of the lattice suggest that we cannot embed the dense order ?
No! The surprising fact is that indeed we can embed the rational line into the power set lattice . Indeed, much more is true—it turns out that we can embed a copy of any countable order whatsoever into the lattice . Every countable order that occurs anywhere at all occurs in the lattice of sets of natural numbers.
Theorem. The power set lattice on the natural numbers is universal for all countable orders. That is, every order relation on a countable domain is isomorphic to a suborder of .
Proof. Let us prove first that every order relation is isomorphic to the subset relation on a collection of sets. Namely, for each let be the down set of , the set of predecessors of :
This is a subset of , and what I claim is that
This is almost immediate. For the forward implication, if , then any order element below is also below , and so . Conversely, if , then since , we must have and hence as desired. So the map is an isomorphism of the original order with the family of all downsets using the subset relation.
To complete the proof, we simply observe that the power set lattice of a countably infinite set is isomorphic to , and for finite it is isomorphic to the power set lattice below a finite set of natural numbers. This is because any bijection of with a set of natural numbers induces a corresponding isomorphism of the respective subsets. So we may find a copy of inside , as desired.
One may make the proof more concrete by combining the two steps, like this: if is any countable order relation, then enumerate the domain set , and for each let . This is like the down set of , except we take the indices of the elements instead of the elements themselves. It follows that if and only if , and so the mapping is an order isomorphism of with the collection of sets under , as desired.
Since the set of rational numbers is countable, it follows as an instance of the universality theorem above that we may find a copy of the rational line inside the power set lattice . Can you find an elegant explicit presentation of rational line in the powerset lattice? In light of the characterization of as a countable endless dense linear order, it will suffice to find any chain in that forms a countable endless dense linear order.
But wait, there is more! We can actually find a copy of the real line in the power set lattice on the naturals! Wait…really? How is that possible? The reals are uncountable, and so this would be an uncountable chain the lattice of sets of natural numbers, but every subset is countable, and there are only countably many elements to add to as you go up. How could there be an uncountable chain in the lattice?
Let me explain.
Theorem. The power set lattice on the natural numbers has an uncountable chain, and indeed, it has a copy of the real continuum .
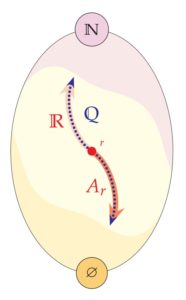
Proof. We have already observed that there must be a copy of the rational line in the power set lattice . In other words, there is a map such that
for any rational numbers .
We may now find our desired copy of the real continuum simply by completing this embedding. Namely, for any real number , let
Since the sets for rational numbers form a chain, it follows easily that implies . And if , then will be strictly contained in some for a rational number strictly between , and consequently strictly contained in . From this, it follows that if and only if , and so we have found a copy of the real number order in the power set lattice, as desired.
Let us now round out the surprising events of this section by proving another shocking fact—we can also find an uncountable antichain in the power set lattice .
Theorem. The power set lattice on the natural numbers has an uncountable antichain, a collection of continuum many pairwise incomparable sets.

Proof. Consider the tree of finite binary sequences . This is the set of all finite binary sequences, ordered by the relation that holds when extends by possibly adding additional binary digits on the end. This is a countable order relation, and so by universality theorem above we may find a copy of it in the power set lattice . But let us be a little more specific. We shall label each node of the tree with a distinct natural number. For any infinite binary path through the tree, let be the set of numbers that appear along the path. Every is infinite, but if , then and will eventually branch away from each other, and consequently and will have only finitely many numbers in common. In particular, neither nor will be a subset of the other, and so we have found an antichain in the powerset lattice. The number of paths through the binary tree is the number of infinite binary sequences, which is the same as the cardinality of the continuum of real numbers, as desired.
So the lattice offers a rich complexity. But is there also homogeneity to be found here? Place yourself at one of the sets in the central region of the lattice, an infinite coinfinite set. There are various new elements for you to add to make a larger set—you can add just this element, or just that one, or any of infinitely many new atoms for you to add to make a larger set. And you could add any combination of those atoms. Above any coinfinite point in the lattice, therefore, one finds a perfect copy of the whole lattice again. Looking upward from any coinfinite set, it always looks the same.
Theorem. The lattice of all sets of natural numbers is homogenous in several respects.
- The lattice of sets above any given coinfinite set is isomorphic to the whole power set lattice .
- The lattice of sets below any given infinite set is isomorphic to the whole power set lattice .
- For any two infinite coinfinite sets , there is an automorphism of the lattice carrying to .

Proof. Let us prove statement (2) first. Consider any infinite set and the sublattice in below it, which is precisely the power set lattice of all subsets of . Since is an infinite set of natural numbers, there is a bijection . We may therefore transform subsets of to subsets of by applying the bijection. Namely, for any define . Since is injective, we have if and only if , and the map maps onto precisely because is surjective, so every is , where . So is an isomorphism of the lattice with , as desired.
For statement (1), consider any cofinite set and let be the part of the power set lattice above , meaning . Since the complement is infinite, there is a bijection of it with the whole set of natural numbers . I claim that the lattice is isomorphic with the lattice , which by statement (1) we know is isomorphic to . To see this, we simply cast out of any set containing . What remains is a subset of , and every subset of will be realized. More specifically, if we define , and observe that if and only if , for the sets already containing . And if , then . So is an isomorphism of the lattice with , which by statement (1) is isomorphic to the whole lattice , as desired.
Finally, let us fix two infinite coinfinite sets . In particular, and are in bijection, as are the complements and . By combining these two bijections, we get a bijection of with itself that carries exactly to , that is, for which . (The reader will have an exercise in my book to give a careful account of this construction.) Because is a bijection of with itself, it induces a corresponding automorphism of the lattice, defined by for . This is an isomorphism of with itself, and , as desired.
Statement (3) of the theorem shows that any two infinite coinfinite sets, being automorphic images of one another, play the same structural role in the lattice —they will have all the same lattice-theoretic properties. In light of this theorem, therefore, one should not look for structure theorems concerning particular sets in the lattice. Rather, the structure theory of is about the structure as a whole, as with the theorems I have proved above.
This is a selection from my book in progress Topics in Logic. It appears in chapter 3, which is on relational logic, and which includes a section on orders with a subsection specifically on the lattice of all sets of natural numbers, because I find it fascinating.







Thanks for the beautiful post, professor — looking forward to the book.
Nitpick: is there a typo in this sentence?
“One generally conceives of the finite sets as clustering near the Earthly bottom of the lattice, finitely close to∅
I believe “coinfinite” should be “cofinite” here.
Yes, thank you! I have now edited.
“many deeply interesting sets such as the prime numbers, the squares, the square-free numbers, the composites, and uncountably many more.”… Really uncountably? Can a (number) set be individually interesting if it isn’t even individualizable, I mean definable? 😁🤔
Second, more concrete question: do you think it’s the countability of N that gives P(N) more interesting lattice-theoretic properties than bigger infinite power sets with inclusion, or do most of those results have higher equivalents to those bigger ones?
Thanks a lot. I am a computer scientist and interested in the following problem. Let (𝑄,≺) be an ordered set with a tree-like Hasse diagram (similar to a prefix tree of a set of strings). Is there any formula to compute the number of antichains (number of subsets of Q composed only of incomparable elements) and the number of maximal antichains (antichains that are not contained in any other antichain) in 𝑄, or at least the lower/upper bounds of these two objects. I know there is a theorem for boolean lattices, but I seek to derive an equivalent one for this special kind of order. BR. Thanks in advance
I don’t know of any simple formula for this case. But in trees, antichains are somewhat simpler and can be recursively generated by replacing any node with an antichain in that upper cone.