This will be a talk January 10, 2017 for the Basic Notions Seminar, aimed at students, post-docs, faculty and guests of the Mathematics Institute, University of Bonn.

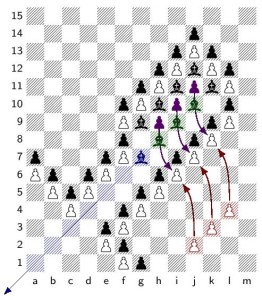
Abstract. I shall give a general introduction to the theory of infinite games, using infinite chess — chess played on an infinite edgeless chessboard — as a central example. Since chess, when won, is won at a finite stage of play, infinite chess is an example of what is known technically as an open game, and such games admit the theory of transfinite ordinal game values. I shall exhibit several interesting positions in infinite chess with very high transfinite game values. The precise value of the omega one of chess is an open mathematical question.  This talk will include some of the latest progress, which includes a position with game value $\omega^4$.

It happens that I shall be in Bonn also for the dissertation defense of Regula Krapf, who will defend the same week, and who is one of the organizers of the seminar.

Transfinite game values in infinite chess | The mate-in-$n$ problem of infinite chess is decidable | A position in infinite chess with game value $\omega^4$ | more on infinite chess | Slides