[bibtex key=EvansHamkinsPerlmutter2017:APositionInInfiniteChessWithGameValueOmega^4]
Abstract. We present a position in infinite chess exhibiting an ordinal game value of $\omega^4$, thereby improving on the previously largest-known values of $\omega^3$ and $\omega^3\cdot 4$.
This is a joint work with Cory Evans and Norman Perlmutter, continuing the research program of my previous article with Evans, Transfinite game values in infinite chess, namely, the research program of finding positions in infinite chess with large transfinite ordinal game values. In the previous article, Cory and I presented a position with game value $\omega^3$. In the current paper, with Norman Perlmutter now having joined us accompanied by some outstanding ideas, we present a new position having game value $\omega^4$, breaking the previous record.
A position in infinite chess with value $\omega^4$
In the new position, above, the kings sit facing each other in the throne room, an uneasy détente, while white makes steady progress in the rook towers. Meanwhile, at every step black, doomed, mounts increasingly desperate bouts of long forced play using the bishop cannon battery, with bishops flying with force out of the cannons, and then each making a long series of forced-reply moves in the terminal gateways. Ultimately, white wins with value omega^4, which exceeds the previously largest known values of omega^3.
In the throne room, if either black or white places a bishop on the corresponding diagonal entryway, then checkmate is very close. A key feature is that for white to place a white-square white bishop on the diagonal marked in red, it is immediate checkmate, whereas if black places a black-square black bishop on the blue diagonal, then checkmate comes three moves later. The bishop cannon battery arrangement works because black threatens to release a bishop into the free region, and if white does not reply to those threats, then black will be three steps ahead, but otherwise, only two.
The throne room
The rook towers are similar to the corresponding part of the previous $\omega^3$ position, and this is where white undertakes most of his main line progress towards checkmate. Black will move the key bishop out as far as he likes on the first move, past $n$ rook towers, and the resulting position will have value $\omega^3\cdot n$. These towers are each activated in turn, leading to a long series of play for white, interrupted at every opportunity by black causing a dramatic spectacle of forced-reply moves down in the bishop cannon battery.
The rook towers
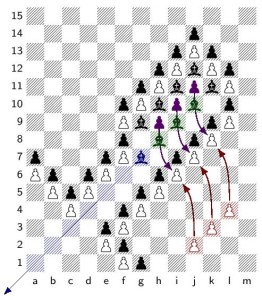
At every opportunity, black mounts a long distraction down in the bishop cannon battery. Shown here is one bishop cannon. The cannonballs fire out of the cannon with force, in the sense that when each green bishop fires out, then white must reply by moving the guard pawns into place.
Bishop cannon
Upon firing, each bishop will position itself so as to attack the entrance diagonal of a long bishop gateway terminal wing. This wing is arranged so that black can make a series of forced-reply threats successively, by moving to the attack squares (marked with the blue squares). Black is threatening to exit through the gateway doorway (in brown), but white can answer the threat by moving the white bishop guards (red) into position. Thus, each bishop coming out of a cannon (with force) can position itself at a gateway terminal of length $g$, making $g$ forced-reply moves in succession. Since black can initiate firing with an arbitrarily large cannon, this means that at any moment, black can cause a forced-reply delay with game value $\omega^2$. Since the rook tower also has value $\omega^2$ by itself, the overall position has value $\omega^4=\omega^2\cdot\omega^2$.
Bishop gateway terminal wing
With future developments in mind, we found that one can make a more compact arrangement of the bishop cannon battery, freeing up a quarter board for perhaps another arrangement that might lead to a higher ordinal values.
Alternative compact version of bishop cannon battery
Read more about it in the article, which is available at the arxiv (pdf).
See also:
- Tranfinite game values in infinite chess
- The mate-in-$n$ problem of infinite chess is decidable
- Johan Wästlund’s MathOverflow question: Checkmate in $\omega$ moves?
- Richard Stanley’s MathOverflow question: Decidability of chess on an infinite board
I don’t get what the bishops marked blue are for. Firing one doesn’t force white to advance a guard pawn. Only green bishops do.
Also, I don’t see how the bishop cannons force a ω² delay. Each only fires up to ω bishops, each with a finite delay.
Yes, the blue bishops are not forced-reply moves, and this is important, because if black had infinitely many immediate forced-reply moves available, then the game would be a draw by infinite play, since black could simply make those moves indefinitely. Rather, for black to move the initial bishop (blue) is to open up a new cannon, and it is precisely after such a move that white gets to make progress in the main line up in the rook towers.
The bishop cannon battery arrangement is a value ω² delay, because black can count down from ω² using it with all forced reply moves (except for the initial move). (And that is essentially what value ω² means; in particular, the checkmate always occurs in finitely many moves, so we are not talking about infinitely long play with the delay). If when counting down from ω², black wants to announce ω*n+k, then he should open up the cannon of size n, and fire the first bishop to a gateway of size k. After the opening move, which is not forced reply, he now has all forced-reply moves that will enable him to count down from this ordinal however he wants. Going from ω*n+k down to ω*n in k moves inside the gateway, he then fires the next green bishop to announce value ω*(n-1)+k’, by moving it to attack gateway k’. And so on. Thus, black can simulate counting down from ω² in this way, with the reusable bishop cannon battery.
Thanks, now I’m clear on the blue bishop’s significance.
But I still don’t get the green bishop. Take a cannon with one green bishop. It can force 6 (?) moves. Two bishops could force 12 moves, three bishops 18, up to ω bishops that force 6ω moves.
Maybe each gateway could be made more and more convoluted, so that a gateway of size ω would take ω moves to get out of it. Use it with a cannon size ω and you’d get a ω² delay.
It seems to me that perhaps there may be some confusion about how game values work. A game has value $\omega$, not because it takes $\omega$ many moves for white to win, but rather because black can announce on his first move an arbitrary number $n$, and play so as to avoid checkmate for at least $n$ moves. White still wins every instance of the game in finitely many moves. If you read the introduction of the paper (click through to the arxiv for a pdf), it explains the game values in terms of such announcements. In particular: white will win in finitely many moves, and none of the plays are infinite, even though they have infinite value. By the way, each green bishop, when it is fired out of the cannon, can force any number of moves, depending on which gateway wing it attacks. So each green bishop, when played, is like an announcement that black is making right then, in terms of how much longer he will be able to play forced-reply moves before the next announcement.
Now I get it! Each bishop attacks a _single_ gateway, that is arbitrarily large, stopping once at each spot marked in blue, thus forcing every white bishop in the gateway to make a move. Thanks.
Yes, that’s right. And each bishop can attack a gateway as big as it wants, when it first moves out of the cannon.
Typo at page 14 of the pdf file on arXiv:
“and so black will advance the pawn at k3 to defend”
should be
“and so white will advance the pawn at k3 to defend”
I read both of your chess papers and was greatly amused. Thank you.
Thanks very much! I have now corrected this in the official version, which will be uploaded to the arxiv later on.
Pingback: Transfinite game values in infinite chess, including new progress, Bonn, January 2017 | Joel David Hamkins
I noticed in another article you co-wrote with C.D.A Evans, “Transfinite Game Values in Infinite Chess”, you say “Namely, in the category of computable play the position is a win for white in the sense that white has a computable strategy that defeats any computable strategy for black;…”
Have you or anyone been able to prove that either FIDE chess, or “Infinite Chess”, is not a win for black? I know that it is probabilistically unlikely, but I’m not interested in a probabilistic conclusion. I’m interested in the results of a formal proof or computer study. There are indeed some games that are a win for the second player, such as Chopsticks, and Nim with the 1-3-5-7 starting position. Also some composed chess positions are a win for black, including some by way of zugzwang. The game of chess itself is not solved, nor do I believe is the game of infinite chess. I am trying to understand how it seems to be that you have concluded that “Infinite Chess” is not a win for black.
On another topic, I was wondering if you would like to play a game of “Chess on an Infinite Plane”. I would suggest a game by online correspondence, one move per day (3 days max), with me updating the diagram after each move.
An example of playing by this format is here:
https://www.chess.com/forum/view/chess960-chess-variants/chess-on-an-infinite-plane-game-cobra91-vickalan
‘https://www.chess.com/forum/view/chess960-chess-variants/chess-on-an-infinite-plane-game-cobra91-vickalan
Thank you for your consideration of my question, and I hope you will play,
In infinite chess, there is no standard starting position, so it doesn’t make sense to say that it is a win for white or black without specifying the starting position. And we have plenty of such positions for which we know it is a win for white or for black. Indeed, the papers where we identify large transfinite ordinal game values are positions that are a win for white starting from that position, and which also exhibit a very high game value, which means that black may nevertheless prolong play in a robust manner.
As for finite 8×8 chess, I am afraid that I have nothing to say about it that Zermelo hadn’t said 100 years ago.
As for infinite correspondence chess, I’m not sure this would work very well, since the most interesting positions occur where there is a very high game value, and for these positions, the losing player may cause arbitrarily long delays in the play, where there would be thousands or millions or more of forced-move play before progress was made in the main line. So while they are extremely interesting mathematically, they are perhaps less interesting to play by post.
Thank you for your reply. Many of your composed positons are indeed very interesting and they do lend themselves to mathematically interesting wins for one side.
My interest is in starting positions where white and black are symmetrical at the start (mirror symmetry or 180° rotational symmetry). In general when the 32 FIDE chess pieces are used, I believe such a game has not been solved. Therefore I don’t believe it is in either player’s interest to cause arbitrarily long delays in the play. White’s best play may be to create attacks, capture pieces, and force a checkmate. Black tries to avoid this, and may have counterplay to win.
One example of a symmetrical setup is in “Chess on an Infinite Plane”, and there’s another which adds two huygens of each color (a piece which jumps prime numbers of squares).
(examples of such games are here):
https://www.chess.com/forum/view/chess960-chess-variants/chess-on-an-infinite-plane-game-cobra91-vickalan
https://www.chess.com/es/forum/view/chess960-chess-variants/chess-on-an-infinite-plane-huygens-option
If you would like to play either game let me know. But if you are too busy with your research of course I understand.
In either case, I would very much appreciate any comment you have about either of the aforementioned starting positions. From what we know neither side starts with a losing position, and therefore it is to neither side’s advantage to play in a way which promotes arbitrarily large numbers of move. Can we at least say that is correct?
Regards, 🙂
Thank you for your comments and the links. And thank you for your kind invitation to play infinite correspondence chess, but unfortunately I am too busy.
OK, thanks Joel.
From what I gather from here and elsewhere is that chess (FIDE) is not solved, and also a chess game on an infinite plane with at least the 32 normal starting pieces with a symmetrical setup is also not solved.
Btw, when expanding chess from the 8×8 board to the infinite board, I think the rule of pawn promotion should be maintained (although I understand the decision is arbitrary). White pawns would promote at rank 8, and black pawns at rank 1 (same as classical chess). Omitting the pawn promotion rule is a rather consequential simplification of the game, and not applying it is an alteration so significant that the game can barely be called “chess” anymore. Nevertheless, your studies of the game on the infinite board are interesting and do expand the knowledge of the game.
Thanks for sharing your very interesting and pioneering research. If you change your mind, and would ever like to play a game of “Chess on an Infinite Plane”, just let me know, 🙂
Best Regards,
Hi Joel,
Another question, in your notable paper “The mate-in-n problem of infinite chess is decidable” (2012), you concluded that chess (with certain restrictions) is decidable.
On page four, you define the scope of the study as “(the) argument relies are: (i) no new pieces enter the board during play, and (ii) the distance pieces—bishops, rooks and queens—move on straight lines whose equations can be expressed using only addition.”
So this bring me to two questions: (1) if pawns promote at ranks 1 and 8 as they do in chess normally, do we know anything about the decidability of infinite chess?
Secondly (2), (and separately), if the huygens is added to the set of chess pieces (a huygens is a chess pieces which jumps prime numbers of squares), again, do way know anything about the decidability of infinite chess?
In the case that the decidability of these versions of chess is unknown, is there any branch of mathematics that can be used to answer such questions, or would such an effort be a futile endeavor?
In infinite chess, usually there is no pawn promotion. But if you want to promote on ranks 1 and 8 (so no pawns allowed outside that narrow band?), then I believe that decidability of the mate-in-n decision problem for finite positions will still work. The huygens piece, however, would break the argument, since the primes are not definable in Presburger arithmetic. So I am not sure whether the mate-in-n problem would still be decidable or not in that case.
Thanks Joel,
Your work is very interesting. Of course you are correct that pawns will be limited to a narrow band if they promote at ranks 1 and 8. But this is only fair, as a pawn is the only piece that can’t move backwards. (Without this rule, a pawn might be doomed to a condition of eternal diminished significance, as things become less interesting far from the normal playing area).
Thanks for your analysis of the decidability of infinite chess, and how it is affected by the huygens. This problem is indeed interesting, just as the knight’s tour problem was interesting in the 9th century. But today’s problems might not lend themselves to solving even with computers. I’ll continue to follow the available resources to see if other pawn promotion rules have been devised (besides the null rule, and the classical rule). I’ll also follow the work on Goldbach’s conjecture, and prime numbers in general, and your work to see if there are any rules devised on how the huygens can best be played in a chess game.
Best regards,