Let me share a mathematical gem with you, the following paradoxical “theorem.”
Theorem. Every triangle is isosceles.
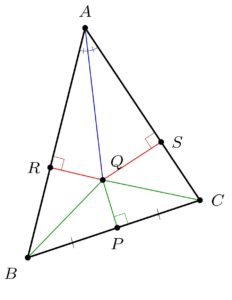
Proof. Consider an arbitrary triangle $\triangle ABC$. Let $Q$ be the intersection of the angle bisector (blue) at $\angle A$ and the perpendicular bisector (green) of $BC$ at midpoint $P$.
Drop perpendiculars from $Q$ to $AB$ at $R$ and to $AC$ at $S$. Because $P$ is the midpoint of $BC$ and $PQ$ is perpendicular, we deduce $BQ\cong CQ$ by the Pythagorean theorem. Since $AQ$ is the angle bisector of $\angle A$, the triangles $AQR$ and $AQS$ are similar, and since they share a hypotenuse, they are congruent. It follows that $AR\cong AS$ and also $QR\cong QS$. Therefore $\triangle BQR$ is congruent to $\triangle CQS$ by the hypotenuse-leg congruence theorem. So $RB\cong SC$. And therefore,
$$AB\cong AR+RB\cong AS+SC\cong AC,$$
and so the triangle is isosceles, as desired. QED
Corollary. Every triangle is equilateral.
Proof. The previous argument proceeded from an arbitrary vertex of the triangle, and so any pair of adjacent sides in the triangle are congruent. So all three are congruent, and therefore it is equilateral. QED
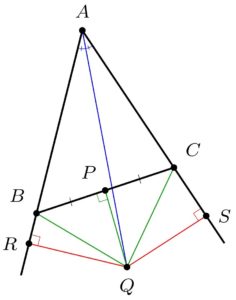
Perhaps you object to my figure, because depending on the triangle, perhaps the angle bisector of $A$ passes on the other side of the midpoint $P$ of $BC$, which would make the point $Q$ lie outside the triangle, as in the following figure.
Nevertheless, essentially the same argument works also in this case. Namely, we again let $Q$ be the intersection of the angle bisector at $\angle A$ with the perpendicular bisector of $BC$ at midpoint $P$, and again drop the perpendiculars from $Q$ to $R$ and $S$. Again, we get $BQ\cong CQ$ by the Pythagorean theorem, using the green triangles. And again, we get $\triangle ARQ\cong\triangle ASQ$ since these are similar triangles with the same hypotenuse. So again, we conclude $\triangle BQR\cong\triangle CQS$ by hypotenuse-leg. So we deduce $AB\cong AR-BR\cong AS-CS\cong AC$, by subtracting rather than adding as before, and so the triangle is isosceles.
Question. What is wrong with these arguments?
Please post your answers in the comments below.
The argument is evidently due to W. W. Rouse Ball, Mathematical Recreations and Essays (1892). I first heard it years ago, when I was in graduate school. Shortly afterward, my advisor W. Hugh Woodin happened to be a little late to seminar, and so I leaped to the chalkboard and gave this proof, leaving the distinguished audience, including R. Solovay, scratching their heads for a while. Woodin arrived, but Solovay wouldn’t let him start the seminar, since he wanted to resolve the triangle argument. What fun!

I certainly had to scratch my head for a long time, but I think I’ve got it now. First, I spotted that if the triangle is isosceles, then the point Q isn’t well-defined. Although I don’t immediately get any conclusion from this observation, it is rather suspicious, and it also means that for many triangles it isn’t easy to guess where Q will be. Anyhow, I then drew a diagram fairly carefully, starting with a right-angled triangle that had one non-hypotenuse side a lot shorter than the other. That enabled me to see that you had pulled the wool over my eyes with your two cases, and in fact, although the lengths that you claimed were equal were indeed equal, I had to subtract one of them and add the other. Since it is false that all triangles are isosceles, and since the rest of the argument appears to be correct, I deduce that this must always be the case.
Indeed, I think you’ve got it. To present the “theorem” to someone else, which is always fun in person, I recommend practicing a little, since you want to draw the figures well enough to make the argument work. My habit is to hold the second case in reserve, in case my audience should actually make that objection, so I can “address” it.
It is slightly hard to disprove the hypothesis that “all triangles are isosceles” by using a triangle that _actually is_ isosceles. 🙂
I had to disabuse my son of this particular argument.
He he, I used to start with this one when I trained the Slovenian math olympiad team. My second problem was: “Where do the bisector of a side and the opposite angle meet?” In any case, when in doubt, draw a very precise picture: https://www.geogebra.org/m/nQ66Ub7j
P. S. You can move the vertices A, B, C to see what happens.
Your geogebra application is great! Did you just write the code for this case now? Wonderful!
I teach Geogebra to students. It took 10 minutes to make your construction (5 of which were spent on getting all the colors right).
Thanks very much for having done so! And I appreciate that you made the colors match my figures. Geogebra seems amazing—I think I’ll have to take it up.
Proving that great minds think alike my first thought was if I try to draw this myself Q is always outside the triangle let’s check that on geogebra.
Second thought was its a great proof by contradiction that Q must be on the outside I don’t need to even think of any further logic.
It isn’t enough merely to note that $Q$ is always outside the triangle, because at the end of my post, I handle the case that $Q$ might be outside. So what was wrong with my reasoning in that case? If you check each step carefully, you will find that all the triangle congruency claims are correct. So what is wrong?
Therefore ZFC is inconsistent! In fact, I think we can even get it all the way to PA being inconsistent!
Finally, we can go home and take a break! 🙂
Very nice. When the perpendiculars are dropped from Q, forming R and S, one point is within the triangle and the other is outside, on the original edge extended. What you call BR and CS are indeed equal in length, but one must be added and the other subtracted. We end up with basically AB = x + y, AC = x – y. This does show that x is the average of AB and AC.
For what is worth, this same “theorem” is presented in Marvin Greenberg’s Euclidean and Non-Euclidean Geometries, Chap. 1, and also in Hartshorne’s Geometry: Euclid and Beyond (p. 36), as a good example of the “danger” in reasoning with diagrams! (Hartshorne attributes the argument to W. W. Rouse Ball’s Mathematical Recreations and Essays, a book from 1892 and revised by Coxeter in 1940.)
Thanks for that earlier reference! I had only had the 1959 Maxwell reference.
No danger in reasoning with diagrams.
“the claim that diagrams are not rigorous mathematical tools starkly conflicts with the fact that ancient mathematical practices, such as the Euclidean one, were greatly successful and free of errors.”
https://web.archive.org/web/20240304033005/https://www.redalyc.org/journal/3397/339767297007/html/
There is much research on this subject. Diagrams have even been automated. (ways have been found to convert them to formal proofs)
The angle bisector and the opposite side’s perpendicular bisector must coincide to give an isosceles triangle. Likewise, all three angle bisectors and their opposite side’s perpendicular bisectors must coincide to give an equilateral triangle. The assumption was there was only one intersection point Q.
Are you saying that in the case there is only one intersection point Q, then the argument works? If this were true, then still it shows that every triangle is isosceles. So your objection can’t be the real problem.
In case there is only one intersection point, point Q and point R must coincide. This creates degenerate triangles, namely △BQR and △CQS. It is impossible to have a degenerate triangle.
It isn’t true in general that Q and R must coincide when those lines have an intersection point, and you can see this by making a careful drawing of the construction. So it seems to me that you don’t yet have your finger on the flaw in the proof.
Thanks to the Geogebra program submitted by Andrej Bauer we can see an isosceles triangle when the angle bisector and opposite side’s perpendicular bisector’s coincide. Also, we can see that when points R and B coincide and points S and Q coincide we have an isosceles triangle with the degenerate triangles mentioned earlier. And when points P and Q coincide the whole triangle degenerates.I really didn’t want to put Q on the outside of the triangle ABC. But once you see the general case requires Q to be outside the triangle, it should be clear the proof is flawed in the segment addition. Well… maybe it wasn’t so obvious!
I think you’ve got it!
If |A-B||A-C|, then R is on the line segment between A and B and C is on the line segment between A and S. [Proof: Let A=(0,0), B=(-b, ab), C=(c, ac), a,b,c>0. Then Q=(0, (b+c)(1+a^2)/2a), R=(-(b+c)/2, a(b+c)/2), S=((b+c)/2, a(b+c)/2).]
I like false proofs, and I enjoyed this problem.
If |A-B| is less than |A-C|, then B is on the line segment between A and R and S is on the line segment between A and C, and if |A-B| is greater than |A-C|, then R is on the line segment between A and B and C is on the line segment between A and S. [Proof: Let A=(0,0), B=(-b, ab), C=(c, ac), a,b,c positive. Then Q=(0, (b+c)(1+a^2)/2a), R=(-(b+c)/2, a(b+c)/2), S=((b+c)/2, a(b+c)/2).]
I like false proofs, and I enjoyed this problem.
Notice we can use it as a (purely geometric) proof that, if ABC is not isocele – which is the condition for Q to be definite – then, if R lies inside the segment AB, S must lie outside AC and vice-versa. For, if they lie both inside or outside, then every triangle is isocele, which is absurd (for we know we CAN drow a triangle which is not isocele).
Pingback: Bütün Üçgenler Aslında İkizkenar Üçgendir! - Bihaber - Son Dakika Haberleri, Daima Güncel Daima Güvenli
Pingback: False Proofs – 20/20 mathematics
I first saw the second “proof” in 1973 when a student showed it to me. Perhaps I was lucky to guess that there was something wrong with the diagram, so when I drew it accurately the solution became clear.
Years later I saw the first “proof” and thought the solution was obvious.
$Q$ would be outside the triangle for non-isosceles triangles, and it would be ambitious when $AB=AC$.
Honestly right triangle is an right triangle, you cant make it isoceles