 My recent talk, Playful Paradox with large numbers, infinity and logic, was a romp through various paradoxical topics in mathematics and logic for an audience of about 150 mathematics and philosophy undergraduate students at Fudan University in Shanghai, and since Fudan is reportedly a top-three university in China, you can expect that the audience was sharp.
My recent talk, Playful Paradox with large numbers, infinity and logic, was a romp through various paradoxical topics in mathematics and logic for an audience of about 150 mathematics and philosophy undergraduate students at Fudan University in Shanghai, and since Fudan is reportedly a top-three university in China, you can expect that the audience was sharp.
For a bit of fun, and in keeping with the theme, we decided to hold a Largest-Number Contest: what is the largest number that one can describe on an ordinary index card?
 My host Ruizhi Yang made and distributed announcement flyers for the contest a week before the talk, with a poster of the talk on one side, and a description of the contest rules on the other, and including a small card to be used for submissions. The rules were as follows:
My host Ruizhi Yang made and distributed announcement flyers for the contest a week before the talk, with a poster of the talk on one side, and a description of the contest rules on the other, and including a small card to be used for submissions. The rules were as follows:
- A submission entry consists of the description of a positive integer written on an ordinary index card, using common mathematical operations and notation or English words and phrases.
- Write legibly, and use at most 100 symbols from the ordinary ASCII character set. Bring your submission to the talk.
- Descriptions that fail to describe a number are disqualified.
- The submission with the largest number wins.
- The prize will be $1 million USD, divided by the winning number itself, rounded to the nearest cent, plus another small token prize.
Example submissions:
$99999$.
$10*(10*99)+5$
The population of Shanghai at this moment.
The submissions were collected at the beginning of my talk, which I began with a nod to Douglas Hofstadter, who once held a similar contest in his column at Scientific American magazine.
To win, I began, it seemed clear that the submitted number must be very large, and since the prize was to be one million dollars divided by the winning number, then this would mean that the prize should become small. So the goal is just to win, and not necessarily to win any money. The real prize is Pride.
So, what kind of numbers should one submit? Of course, anyone could think to write $99999$, or one million ($10^6$), one billion ($10^9$) or one trillion ($10^{12}$). Perhaps someone would want to write a googol, which is a common name for $10^{100}$. Written in decimal, this is $$10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000,$$ which is one character too long for the rules, so one should use the more compact formulations. But let’s just write it as googol.
But we can easily describe much larger numbers. A googol plex is the number $10^{\text{googol}}$, written in decimal with a $1$ followed by a googol many $0$s. A googol plex is also describable as $10^{10^{100}}$. An iterated exponential $a^{b^c}$ could be seen as ambiguous, referring either to $(a^b)^c$ or to $a^{(b^c)}$. These are not always the same, and so exponentiation is not an associative operation. But which is bigger? If the aim is to make big numbers, then generally one wants to have as big an exponent as possible, and so $a^{(b^c)}$ will be much larger than $(a^b)^c$, which is just $a^{bc}$, and so we will always associate our exponentials upward. (Nevertheless, the upward associated form is not always larger, which you can see in the case of $2^{1^{100}}$.) In general, we can apply the plex operation to any number, so $x$ plex just means $10^x$.
A googol bang means googol !, or googol factorial, the number obtained by multiplying googol $\cdot$ (googol -1) $\cdots 2\cdot 1$, and in general, $x$ bang means $x!$. Which is bigger, a googol plex or a googol bang? If you think about it, a googol plex is 10 times 10 times 10, and so on, with a googol number of terms. Meanwhile, the factorial googol bang also has a googol terms in it, but most of them (except for 10) are far larger than 10, so it is clear that a googol bang is much larger than a googol plex.
Continuing down this road, how about a googol plex bang, or a googol bang plex? Which of these is larger? Please turn away and think about it for a bit……..Have you got it? I think like this: A googol plex bang has the form $(10^g)!$, which is smaller than $(10^g)^{10^g}$, which is equal to $10^{g10^g}$, and this is smaller than $10^{g!}$ when $g$ is large. So a googol plex bang is smaller than a googol bang plex.
There is an entire hierarchy of such numbers, such as googol bang plex bang bang bang and googol bang bang plex plex plex. Which of these is bigger? Do you have a general algorithm for determining which of two such expressions is larger?
A googol stack is the number
$$10^{10^{10^{\cdot^{\cdot^{10}}}}}{\large\rbrace} \text{ a stack of height googol},$$
where the height of the exponential stack is googol. Similarly, we may speak of $x$ stack for any $x$, and form such expressions as:
googol stack bang plex
googol bang plex stack
googol plex stack bang
Which of these is larger? If you think about it, you will see that the stack operator is far more powerful than bang or plex, and so we want to apply it to the biggest possible argument. So the second number is largest, and then the third and then the first, simply because the stack operator will overrule the other effects. Let us call this hierarchy, of all expressions formed by starting with googol and then appending any number of plex, bang or stack operators, as the googol plex bang stack hierarchy.
Question. Is there a feasible computational procedure to determine, of any two expressions in the googol stack bang plex hierarchy, which is larger?
This is an open question in the general case. I had asked this question at math.stackexchange, Help me put these enormous numbers in order, and the best currently known (due to user Deedlit) is that we have a simple algorithm that works for all expressions of length at most googol-2, and also works for all expressions having the same number of operators. But this algorithm breaks down for large expressions of much different lengths, since it seems that one must come to know the exact threshold where an enormous iteration of bangs and plexes can ultimately capture a stack. Of course, in principle one can compute these numbers exactly, given sufficient time and space resources, but the point of the question is to have a feasible algorithm, such as one that takes only polynomial time in the length of the input expressions. And a feasible such general algorithm is not known.
The fact that we seem to have difficulty comparing the relative sizes of expressions even in the simple googol plex bang stack hierarchy suggests that we may find it difficult to select a winning entry in the largest-number contest. And indeed, I’ll explain a bit later why there is no computable procedure to determine the winner of arbitrary size largest-number contests.
The numbers we’ve seen so far are actually rather small, so let’s begin to describe some much larger numbers. The most basic operation on natural numbers is the successor operation $a\mapsto a+1$, and one can view addition as repeated succession:
$$a+b=a+\overbrace{1+1+\cdots+1}^{b\text{ times}}.$$
Similarly, multiplication is repeated addition
$$a\cdot b=\overbrace{a+a+\cdots+a}^{b\text{ times}}$$
and exponentiation is repeated multiplication
$$a^b=\overbrace{a\cdot a\cdots a}^{b\text{ times}}.$$
Similarly, stacks are repeated exponentiation. To simplify the expressions, Knuth introduced his uparrow notation, writing $a\uparrow b$ for $a^b$, and then repeating it as
$$a\uparrow\uparrow b=\overbrace{a\uparrow a\uparrow\cdots\uparrow a}^{b\text{ times}}= a^{a^{a^{.^{.^a}}}}{\large\rbrace}{ b\text{ times}}.$$
So googol stack is the same as $10\uparrow\uparrow$ googol. But why stop here, we can just as easily define the triple repeated uparrow
$$a\uparrow\uparrow\uparrow b=\overbrace{a\uparrow\uparrow a\uparrow\uparrow\ \cdots\ \uparrow\uparrow a}^{b\text{ times}}.$$
In this notation, $10\uparrow\uparrow\uparrow$ googol means
$$\overbrace{10^{10^{.^{.^{10}}}}{\large\rbrace}10^{10^{.^{.^{10}}}}{\large\rbrace}10^{10^{.^{.^{10}}}}{\large\rbrace}\cdots\cdots{\large\rbrace} 10^{10^{.^{.^{10}}}}{\large\rbrace}10}^{\text{iterated googol times}},$$
where the number of times the stacking process is iterated is googol. This number is a vast number, whose description $10\uparrow\uparrow\uparrow$ googol fits easily on an index card.
But why stop there? We could of course continue with $10\uparrow\uparrow\uparrow\uparrow$ googol and so on, but I’d rather define
$$10\Uparrow x=10\ \overbrace{\uparrow\uparrow\cdots\uparrow}^{x\text{ times}}\ 10.$$
So that $10\Uparrow$ googol is vaster than anything we’ve mentioned above. But similarly, we will have $10\Uparrow\Uparrow$ googol and so on, leading eventually to a triple uparrow
$$10 \uparrow\hskip-.55em\Uparrow\text{ googol } = 10 \overbrace{\Uparrow\Uparrow\cdots\Uparrow}^{\text{googol iterations}} 10,$$
and so on. These ideas lead ultimately to the main line of the Ackerman function.
So we’ve described some truly vast numbers. But what is the winning entry? After all, there are only finitely many possible things to write on an index card in accordance with the limitation on the number of symbols. Many of these possible entries do not actually describe a number–perhaps someone might submit a piece of poetry or confess their secret love–but nevertheless among the entries that do describe numbers, there are only finitely many. Thus, it would seem that there must be a largest one. Thus, since the rules expressly allow descriptions of numbers in English, it would seem that we have found our winning entry:
The largest number describable on an index card according to the rules of this contest
which uses exactly 86 symbols. We seem to have argued that this expression describes a particular number, and accords with the rules, so we conclude that this is indeed provably the winning entry.
But wait a minute! If the expression above describes a number, then it would seem that the following expression also describes a number:
The largest number describable on an index card according to the rules of this contest, plus one
which uses 96 symbols. And this number would seem to be larger, by exactly one, of the number which we had previously argued must be the largest number that is possible to describe on an index card. Indeed, how are we able to write this description at all? We seem to have described a number, while following certain rules, that is strictly larger than any number which it is possible to describe while following those rules. Contradiction! This conundrum is known as Berry’s paradox, the paradox of “the smallest positive integer not definable in under eleven words.”
Thus, we can see that this formulation of the largest-number contest is really about the Berry paradox, which I shall leave you to ponder further on your own.
I concluded this part of my talk by discussing the fact that even when one doesn’t allow natural language descriptions, but stays close to a formal language, such as the formal language of arithmetic, then the contest ultimately wades into some difficult waters of mathematical logic. It is a mathematical theorem that there is no computable procedure that will correctly determine which of two descriptions, expressed in that formal language, describes the larger natural number. For example, even if we allow descriptions of the form, “the size of the smallest integer solution to this integer polynomial equation $p(x_1,\ldots,x_k)=0$,” where $p$ is provided as a specific integer polynomial in several variables. The reason is that the halting problem of computability theory is undecidable, and it is reducible to the problem of determining whether such a polynomial equation has a solution, and when it does, the size of the smallest solution is related to the halting time of the given instance of the halting problem. Worse, the independence phenomenon shows that not only is the comparison problem undecidable, but actually there can be specific instances of descriptions of numbers in these formal languages, such that both definitely describe a specific number, but the question of which of the two numbers described is larger is simply independent of our axioms, whatever they may be. That is, the question of whether one description describes a larger number than another or not may simply be neither provable nor refutable in whatever axiomatic system we have chosen to work in, no matter how strong. In such a case, I would find it to be at least a debatable philosophical question whether there is indeed a fact of the matter about whether one of the numbers is larger than the other or not. (See my explanation here). It is my further considered belief that every largest-number contest, taken seriously, unless severely limited in the scope of the descriptions that entries may employ, will founder on precisely this kind of issue.
For further reading on this topic, there are a number of online resources:
Googol plex bang stack hierarchy | Largest number contest on MathOverflow
Scott Aaronson on Big Numbers (related: succinctly naming big numbers)
Meanwhile, lets return to our actual contest, for which we collected a number of interesting submissions, on which I’ll comment below. Several students had appreciated the connection between the contest and Berry’s paradox.
 Your number is quite large, since we can surely describe an enormous number of digits of $\pi$. Researchers have announced, for example, that they have now found 10 trillion digits of $\pi$. If by “describe physically” you meant that we should say the digits aloud, however, then supposing that we speak very quickly and say five digits per second (which is quite a lot if sustained for any length of time), then one person would be able to pronounce a little over 4 million digits this way in 10 days. If all humanity were to speak digits in parallel, then we could rise up to the order of $10^{16}$ digits in ten days. This is a big number indeed, although not nearly as big as a googol or many of the other numbers we have discussed.
Your number is quite large, since we can surely describe an enormous number of digits of $\pi$. Researchers have announced, for example, that they have now found 10 trillion digits of $\pi$. If by “describe physically” you meant that we should say the digits aloud, however, then supposing that we speak very quickly and say five digits per second (which is quite a lot if sustained for any length of time), then one person would be able to pronounce a little over 4 million digits this way in 10 days. If all humanity were to speak digits in parallel, then we could rise up to the order of $10^{16}$ digits in ten days. This is a big number indeed, although not nearly as big as a googol or many of the other numbers we have discussed.
 Surely $\infty$ is a large number, but it is not ordinarily considered to be a positive integer or a natural number. And so I think that your submission does not accord with the rules.
Surely $\infty$ is a large number, but it is not ordinarily considered to be a positive integer or a natural number. And so I think that your submission does not accord with the rules.
 This is charming, and I’m sure that your girlfriend will be very happy to see this. Depending on the units we use to measure your affection, I find it very likely that this number is extremely large indeed, and perhaps you win the contest. (But in order to stay within the rules, we should pick the units so that your affection comes out exactly as a positive integer; in particular, if your affection is actually infinite, as you seem to indicate, then I am afraid that you would be disqualified.) One concern that I have, however, about your delightful entry—please correct me if I am wrong—is this: did you write at first about your affection for your “girlfriends” (plural), and then cross out the extra “s” in order to refer to only one girlfriend? And when you refer to your “girlfriend(s), which values at least $\omega$,” do you mean to say that your affection for each girlfriend separately has value $\omega$, or are you instead saying that you have affection for $\omega$ many girlfriends? I’m not exactly sure. But either interpretation would surely lead to a large number, and it does seem quite reasonable that one might indeed have more affection, if one had many girlfriends rather than only one! I suppose we could accept this entry as a separate submission about your affection, one value for each girlfriend separately, but perhaps it may be best to combine all your affection together, and consider this as one entry. In any case, I am sure that you have plenty of affection.
This is charming, and I’m sure that your girlfriend will be very happy to see this. Depending on the units we use to measure your affection, I find it very likely that this number is extremely large indeed, and perhaps you win the contest. (But in order to stay within the rules, we should pick the units so that your affection comes out exactly as a positive integer; in particular, if your affection is actually infinite, as you seem to indicate, then I am afraid that you would be disqualified.) One concern that I have, however, about your delightful entry—please correct me if I am wrong—is this: did you write at first about your affection for your “girlfriends” (plural), and then cross out the extra “s” in order to refer to only one girlfriend? And when you refer to your “girlfriend(s), which values at least $\omega$,” do you mean to say that your affection for each girlfriend separately has value $\omega$, or are you instead saying that you have affection for $\omega$ many girlfriends? I’m not exactly sure. But either interpretation would surely lead to a large number, and it does seem quite reasonable that one might indeed have more affection, if one had many girlfriends rather than only one! I suppose we could accept this entry as a separate submission about your affection, one value for each girlfriend separately, but perhaps it may be best to combine all your affection together, and consider this as one entry. In any case, I am sure that you have plenty of affection.
 You’ve submitted Graham’s number, an extremely large number that is also popularly known as the largest definite number ever to be used in a published mathematical proof. This number is certainly in the upper vicinity of the numbers we discussed above, obtained by iterating the Knuth uparrow. It is much larger than anything we can easily write in the googol plex bang stack hierarchy. This is essentially in line with iterating the $\Uparrow$ operator $64$ times, using base $3$. This number is extremely large, and I find it to be the largest number submitted by means of a definite description whose numerical value does not depend on which other numbers have been submitted to the contest. Meanwhile, we discussed some even larger numbers above, such as the triple uparrow $10 \uparrow\hskip-.55em\Uparrow$ googol.
You’ve submitted Graham’s number, an extremely large number that is also popularly known as the largest definite number ever to be used in a published mathematical proof. This number is certainly in the upper vicinity of the numbers we discussed above, obtained by iterating the Knuth uparrow. It is much larger than anything we can easily write in the googol plex bang stack hierarchy. This is essentially in line with iterating the $\Uparrow$ operator $64$ times, using base $3$. This number is extremely large, and I find it to be the largest number submitted by means of a definite description whose numerical value does not depend on which other numbers have been submitted to the contest. Meanwhile, we discussed some even larger numbers above, such as the triple uparrow $10 \uparrow\hskip-.55em\Uparrow$ googol.
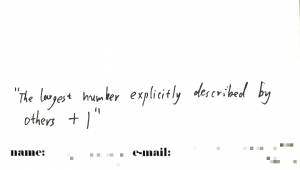 Your clever submission shows that you realize that it isn’t necessary to actually mention the largest possible number to describe, as we discussed in Berry’s paradox above, but it suffices rather to exceed only the largest actually occurring numbers that are described by others in the contest. What are we to do, however, when two people have this same clever idea? If either of them succeeds in describing a number, then it would seem that they both must succeed, but in this case, they must both have described numbers larger than the other. This is the same contradiction at the heart of Berry’s paradox. Another risky feature of this entry is that it presumes that some numbers were in fact described by others. How are we to interpret it if all other submissions are disqualified?
Your clever submission shows that you realize that it isn’t necessary to actually mention the largest possible number to describe, as we discussed in Berry’s paradox above, but it suffices rather to exceed only the largest actually occurring numbers that are described by others in the contest. What are we to do, however, when two people have this same clever idea? If either of them succeeds in describing a number, then it would seem that they both must succeed, but in this case, they must both have described numbers larger than the other. This is the same contradiction at the heart of Berry’s paradox. Another risky feature of this entry is that it presumes that some numbers were in fact described by others. How are we to interpret it if all other submissions are disqualified?
 Your description has the very nice feature that it avoids the self-reference needed in the previous description to refer to all the “other” entries (that is, all the entries that are not “this” one). It avoids the self-reference by speaking of “second-largest” entry, which of course will have to be the largest of the other entries, since this entry is to be one larger. Although it avoids self-reference, nevertheless this description is what would be called impredicative, because it quantifies over a class of objects (the collected entries) of which it is itself a member. Once one interprets things as you seem to intend, however, this entry appears to amount to essentially the same description as the previous entry. Thus, the problematic and paradoxical situation has now actually occurred, making it problematic to conclude that either of these entries has succeeded in describing a definite number. So how are we to resolve it?
Your description has the very nice feature that it avoids the self-reference needed in the previous description to refer to all the “other” entries (that is, all the entries that are not “this” one). It avoids the self-reference by speaking of “second-largest” entry, which of course will have to be the largest of the other entries, since this entry is to be one larger. Although it avoids self-reference, nevertheless this description is what would be called impredicative, because it quantifies over a class of objects (the collected entries) of which it is itself a member. Once one interprets things as you seem to intend, however, this entry appears to amount to essentially the same description as the previous entry. Thus, the problematic and paradoxical situation has now actually occurred, making it problematic to conclude that either of these entries has succeeded in describing a definite number. So how are we to resolve it?
 Your description is very clever, trying to have it both ways. Of course, every participant in the contest wants to win, but you also to win with a very low winning number, so that you can maximize the prize payout. With this submission, of course you hope that all other submissions might be disqualified, in which case you will win with the number 1, achieving the million dollar payout! In the case of our actual contest, however, there are other cards that are qualified, such as the Graham’s number submission, and so your submission seems to be in case 2, making it similar in effect to the previous submission. Like the previous two entries, this card is problematic when two or more players submit the same description. And indeed, even with the other descriptions submitted above, we are already placed into the paradoxical situation that if this card describes a number in its case 2, then it will be larger than some numbers that are larger than it.
Your description is very clever, trying to have it both ways. Of course, every participant in the contest wants to win, but you also to win with a very low winning number, so that you can maximize the prize payout. With this submission, of course you hope that all other submissions might be disqualified, in which case you will win with the number 1, achieving the million dollar payout! In the case of our actual contest, however, there are other cards that are qualified, such as the Graham’s number submission, and so your submission seems to be in case 2, making it similar in effect to the previous submission. Like the previous two entries, this card is problematic when two or more players submit the same description. And indeed, even with the other descriptions submitted above, we are already placed into the paradoxical situation that if this card describes a number in its case 2, then it will be larger than some numbers that are larger than it.
 Your submission is very ambitious, attempting both to win and to win the most money. (I take the description as the lower part of this card, and the upper note is a remark about it.) You seem to realize that there will be ties in the game, with multiple people submitting a winning entry. And indeed, if everyone had submitted this entry, then the winning number would indeed seem to be 1, which is the smallest number that would make them all be one of the members who win the game, so the million dollars would be split amongst that group. Some clumsy person, however, might submit a googol plex bang, however, which would bump up the value of this card to that same value, which although still winning, would win much less money. Your line of reasoning about rationality is very similar to the concept of superrationality defended by Douglas Hofstadter in the context of the prisoner’s dilemma. Perhaps one might also be tempted to say something like:
Your submission is very ambitious, attempting both to win and to win the most money. (I take the description as the lower part of this card, and the upper note is a remark about it.) You seem to realize that there will be ties in the game, with multiple people submitting a winning entry. And indeed, if everyone had submitted this entry, then the winning number would indeed seem to be 1, which is the smallest number that would make them all be one of the members who win the game, so the million dollars would be split amongst that group. Some clumsy person, however, might submit a googol plex bang, however, which would bump up the value of this card to that same value, which although still winning, would win much less money. Your line of reasoning about rationality is very similar to the concept of superrationality defended by Douglas Hofstadter in the context of the prisoner’s dilemma. Perhaps one might also be tempted to say something like:
the smallest number that makes me win, with the largest possible prize payout to me.
with the idea that you’d get a bigger prize solely for yourself if you avoided a tie situation by adding one more, so as to get the whole prize for yourself. But if this reasoning is correct, then one would seem to land again in the clutches of the Berry paradox.
To my readers: please make your submissions or comments below!









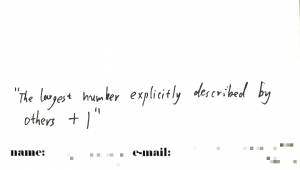








 This will be a talk for specialists in philosophy, mathematics and the philosophy of mathematics, given as part of the workshop
This will be a talk for specialists in philosophy, mathematics and the philosophy of mathematics, given as part of the workshop 
 This will be a short lecture series given at the conclusion of the graduate logic class in the
This will be a short lecture series given at the conclusion of the graduate logic class in the 
