[bibtex key=”GitmanHamkinsHolySchlichtWilliams2020:The-exact-strength-of-the-class-forcing-theorem”]
Abstract. The class forcing theorem, which asserts that every class forcing notion
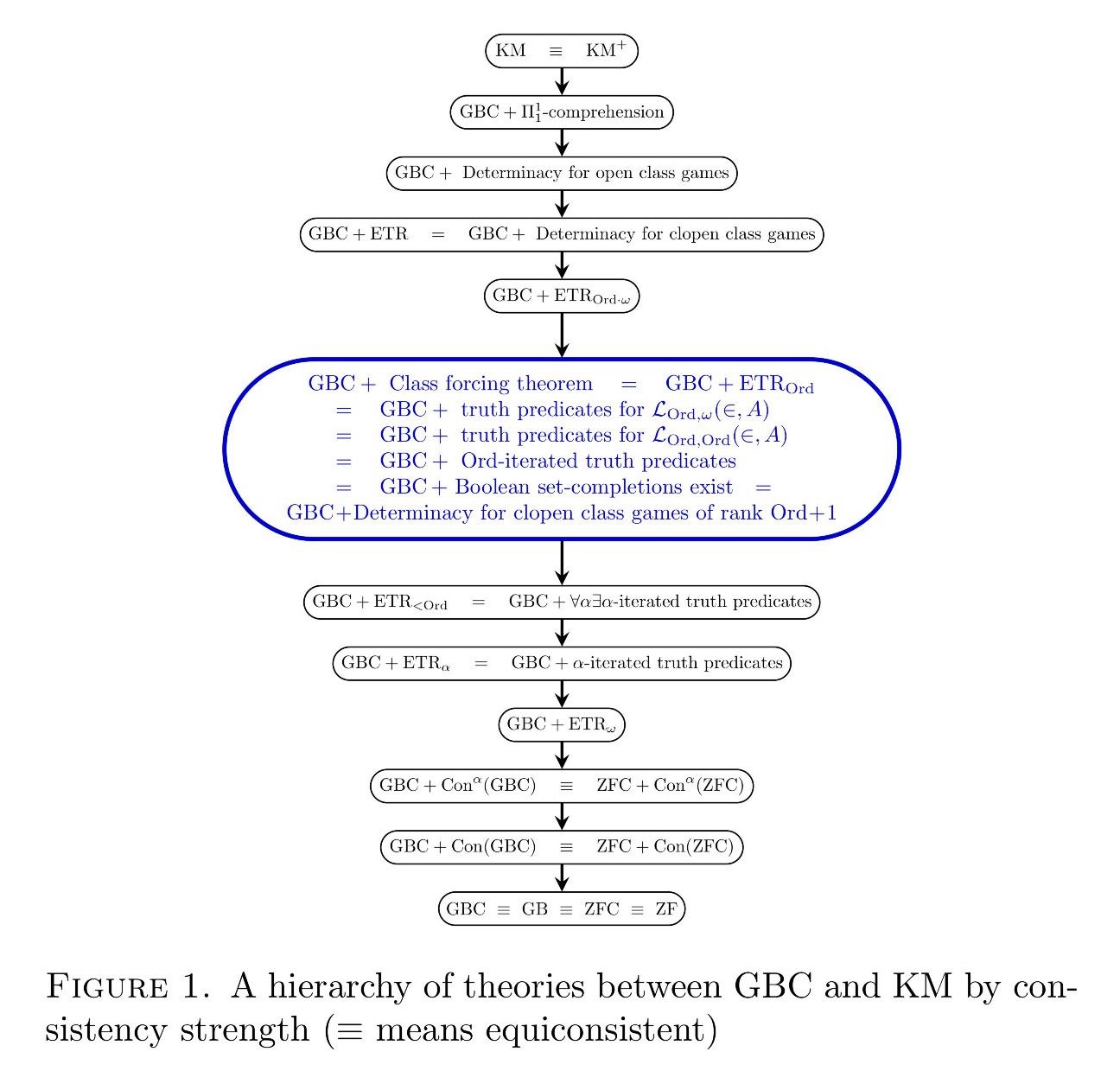
admits a forcing relation ℙ , that is, a relation satisfying the forcing relation recursion — it follows that statements true in the corresponding forcing extensions are forced and forced statements are true — is equivalent over Gödel-Bernays set theory GBC to the principle of elementary transfinite recursion ⊩ ℙ for class recursions of length E T R O r d . It is also equivalent to the existence of truth predicates for the infinitary languages O r d , allowing any class parameter L O r d , 𝜔 ( ∈ , 𝐴 ) ; to the existence of truth predicates for the language 𝐴 ; to the existence of L O r d , O r d ( ∈ , 𝐴 ) -iterated truth predicates for first-order set theory O r d ; to the assertion that every separative class partial order L 𝜔 , 𝜔 ( ∈ , 𝐴 ) has a set-complete class Boolean completion; to a class-join separation principle; and to the principle of determinacy for clopen class games of rank at most ℙ . Unlike set forcing, if every class forcing relation O r d + 1 has a forcing relation merely for atomic formulas, then every such ℙ has a uniform forcing relation that applies uniformly to all formulas. Our results situate the class forcing theorem in the rich hierarchy of theories between GBC and Kelley-Morse set theory KM. ℙ
We shall characterize the exact strength of the class forcing theorem, which asserts that every class forcing notion
Unlike the case of set forcing, where one may prove in ZFC that every set forcing notion has corresponding forcing relations, for class forcing it is consistent with Gödel-Bernays set theory GBC that there is a proper class forcing notion lacking a corresponding forcing relation, even merely for the atomic formulas. For certain forcing notions, the existence of an atomic forcing relation implies Con(ZFC) and much more, and so the consistency strength of the class forcing theorem strictly exceeds GBC, if this theory is consistent. Nevertheless, the class forcing theorem is provable in stronger theories, such as Kelley-Morse set theory. What is the exact strength of the class forcing theorem?
Our project here is to identify the strength of the class forcing theorem by situating it in the rich hierarchy of theories between GBC and KM, displayed in part in the figure above, with the class forcing theorem highlighted in blue. It turns out that the class forcing theorem is equivalent over GBC to an attractive collection of several other natural set-theoretic assertions; it is a robust axiomatic principle.
The main theorem is naturally part of the emerging subject we call the reverse mathematics of second-order set theory, a higher analogue of the perhaps more familiar reverse mathematics of second-order arithmetic. In this new research area, we are concerned with the hierarchy of second-order set theories between GBC and KM and beyond, analyzing the strength of various assertions in second-order set theory, such as the principle ETR of elementary transfinite recursion, the principle of
Main Theorem. The following are equivalent over Gödel-Bernays set theory.
- The atomic class forcing theorem: every class forcing notion admits forcing relations for atomic formulas
𝑝 ⊩ 𝜎 = 𝜏 𝑝 ⊩ 𝜎 ∈ 𝜏 . - The class forcing theorem scheme: for each first-order formula
𝜑 ˙ Γ 𝑖
𝑝 ⊩ 𝜑 ( ⃗ 𝜏 , ˙ Γ 0 , … , ˙ Γ 𝑚 ) . - The uniform first-order class forcing theorem: every class forcing notion
ℙ 𝑝 ⊩ 𝜑 ( ⃗ 𝜏 ) , 𝜑 L 𝜔 , 𝜔 ( ∈ , 𝑉 ℙ , ˙ Γ 0 , … , ˙ Γ 𝑚 ) - The uniform infinitary class forcing theorem: every class forcing notion
ℙ 𝑝 ⊩ 𝜑 ( ⃗ 𝜏 ) , 𝜑 L O r d , O r d ( ∈ , 𝑉 ℙ , ˙ Γ 0 , … , ˙ Γ 𝑚 ) - Names for truth predicates: every class forcing notion
ℙ ˙ T 1 ⊩ ˙ T L 𝜔 , 𝜔 ( ∈ , 𝑉 ℙ , ˙ Γ 0 , … , ˙ Γ 𝑚 ) - Every class forcing notion
ℙ 𝔹 ℙ - The class-join separation principle plus
E T R O r d - For every class
𝐴 L O r d , 𝜔 ( ∈ , 𝐴 ) - For every class
𝐴 L O r d , O r d ( ∈ , 𝐴 ) - For every class
𝐴 O r d L 𝜔 , 𝜔 ( ∈ , 𝐴 ) - The principle of determinacy for clopen class games of rank at most
O r d + 1 - The principle
E T R O r d O r d
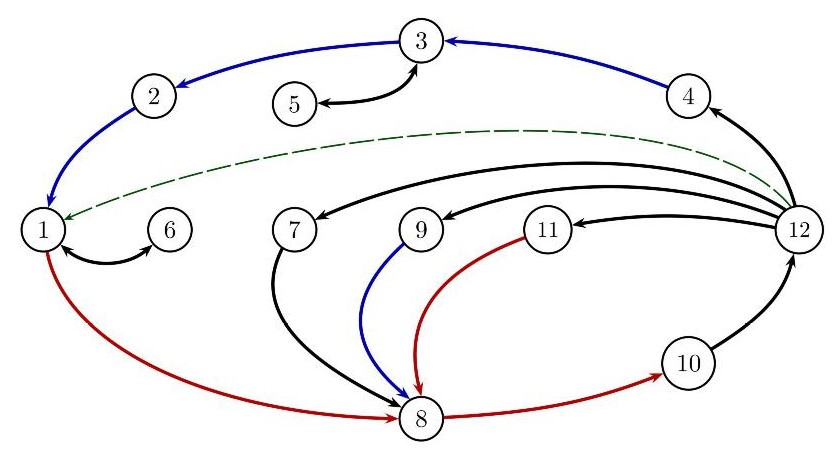
We prove the theorem by establishing the complete cycle of indicated implications. The red arrows indicate more difficult or substantive implications, while the blue arrows indicate easier or nearly immediate implications. The green dashed implication from statement (12) to statement (1), while not needed for the completeness of the implication cycle, is nevertheless used in the proof that (12) implies (4). The proof of (12) implies (7) also uses (8), which follows from the fact that (12) implies (9) implies (8).
For more, download the paper from the arxiv: [bibtex key=”GitmanHamkinsHolySchlichtWilliams:The-exact-strength-of-the-class-forcing-theorem”]
See also Victoria’s post, Kameryn’s post.