[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]
Abstract. The principle of open class determinacy is preserved by pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Similarly, the principle of elementary transfinite recursion ETR for a fixed class well-order is preserved by pre-tame class forcing. The full principle ETR itself is preserved by countably strategically closed pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Meanwhile, it remains open whether ETR is preserved by all forcing, including the forcing merely to add a Cohen real.
The principle of elementary transfinite recursion ETR — according to which every first-order class recursion along any well-founded class relation has a solution — has emerged as a central organizing concept in the hierarchy of second-order set theories from Gödel-Bernays set theory GBC up to Kelley-Morse set theory KM and beyond. Many of the principles in the hierarchy can be seen as asserting that certain class recursions have solutions.
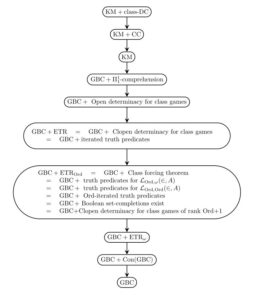
In addition, many of these principles, including ETR and its variants, are equivalently characterized as determinacy principles for certain kinds of class games. Thus, the hierarchy is also fruitfully unified and organized by determinacy ideas.
This hierarchy of theories is the main focus of study in the reverse mathematics of second-order set theory, an emerging subject aiming to discover the precise axiomatic principles required for various arguments and results in second-order set theory. The principle ETR itself, for example, is equivalent over GBC to the principle of clopen determinacy for class games and also to the existence of iterated elementary truth predicates (see Open determinacy for class games); since every clopen game is also an open game, the principle ETR is naturally strengthened by the principle of open determinacy for class games, and this is a strictly stronger principle (see Hachtman and Sato); the weaker principle ETR, meanwhile, asserting solutions to class recursions of length Ord, is equivalent to the class forcing theorem, which asserts that every class forcing notion admits a forcing relation, to the existence of set-complete Boolean completions of any class partial order, to the existence of Ord-iterated elementary truth predicates, to the determinacy of clopen games of rank at most Ord+1, and to other natural set-theoretic principles (see The exact strength of the class forcing theorem).
Since one naturally seeks in any subject to understand how one’s fundamental principles and tools interact, we should like in this article to consider how these second-order set-theoretic principles are affected by forcing. These questions originated in previous work of Victoria Gitman and myself, and question 1 also appears in the dissertation of Kameryn Williams, which was focused on the structure of models of second-order set theories.
It is well-known, of course, that ZFC, GBC, and KM are preserved by set forcing and by tame class forcing, and this is true for other theories in the hierarchy, such as GBC-comprehension and higher levels of the second-order comprehension axiom. The corresponding forcing preservation theorem for ETR and for open class determinacy, however, has not been known.
Question 1. Is ETR preserved by forcing?
Question 2. Is open class determinacy preserved by forcing?
We intend to ask in each case about class forcing as well as set forcing. Question 1 is closely connected with the question of whether forcing can create new class well-order order types, longer than any class well-order in the ground model. Specifically, Victoria Gitman and I had observed earlier that ETR for a specific class well-order is preserved by pre-tame class forcing, and this would imply that the full principle ETR would also be preserved, if no fundamentally new class well-orders are created by the forcing. In light of the fact that forcing over models of ZFC adds no new ordinals, that would seem reasonable, but proof is elusive, and the question remains open. Can forcing add new class well-orders, perhaps very tall ones that are not isomorphic to any ground model class well-order? Perhaps there are some very strange models of GBC that gain new class well-order order types in a forcing extension.
Question 3. Assume GBC. After forcing, must every new class well-order be isomorphic to a ground-model class well-order? Does ETR imply this?
The main theorem of this article provides a full affirmative answer to question 2, and partial affirmative answers to questions 2 and 3.
Main Theorem.
- Open class determinacy is preserved by pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.
- The principle ETR, for any fixed class well order , is preserved by pre-tame class forcing.
- The full principle ETR is preserved by countably strategically closed pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.
We should like specifically to highlight the fact that questions 1 and 3 remain open even in the case of the forcing to add a Cohen real. Is ETR preserved by the forcing to add a Cohen real? After adding a Cohen real, is every new class well-order isomorphic to a ground-model class well-order? One naturally expects affirmative answers, especially in a model of ETR.
For more, click through the arxiv for a pdf of the full article.
[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]





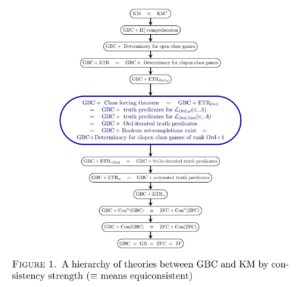

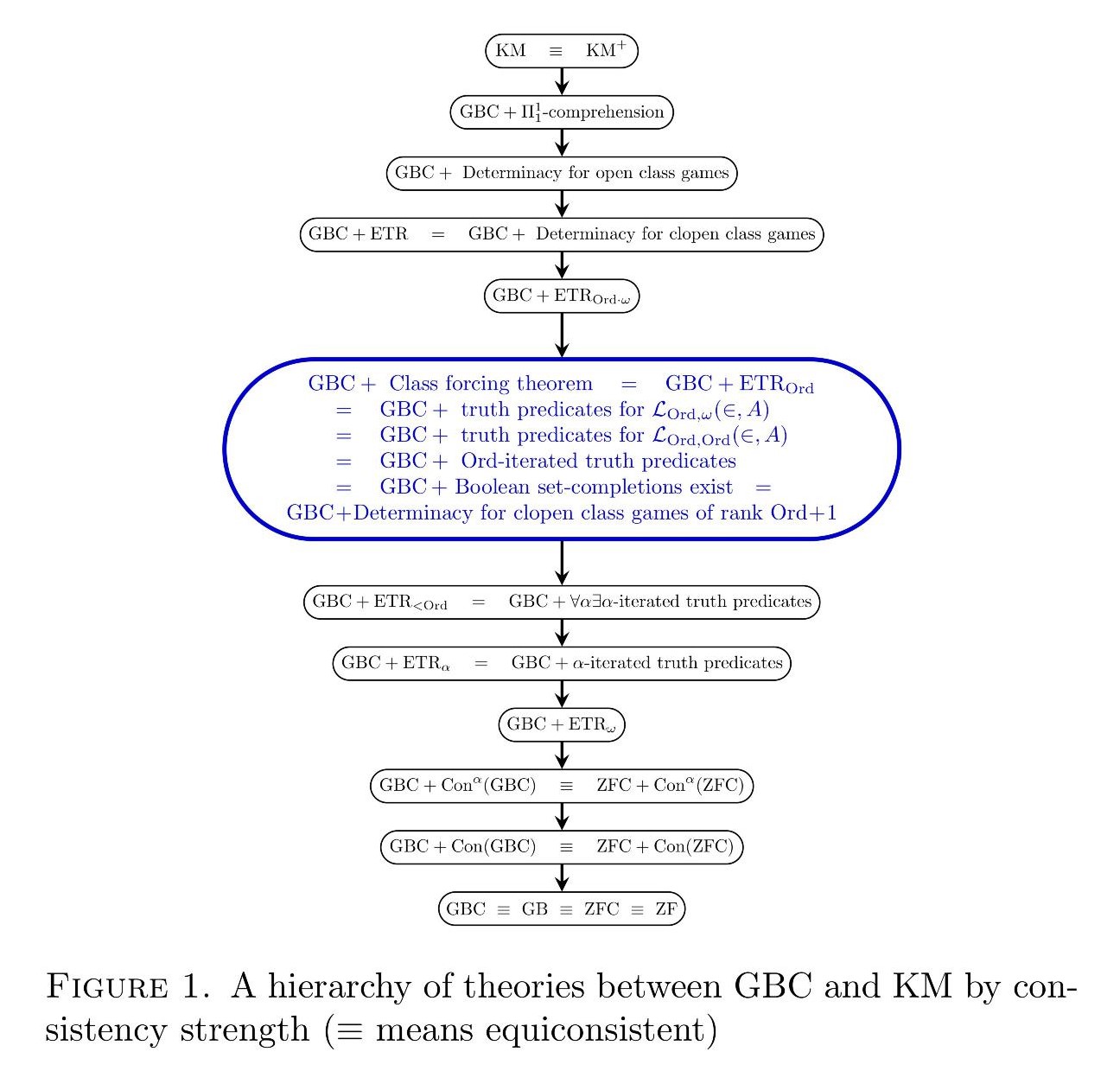

 This is joint work with Victoria Gitman. See our article,
This is joint work with Victoria Gitman. See our article, 
