This will be a talk at the XVII International Luminy Workshop in Set Theory at the Centre International de Rencontres Mathématiques (CIRM) near Marseille, France, held 9-13 October 2023.
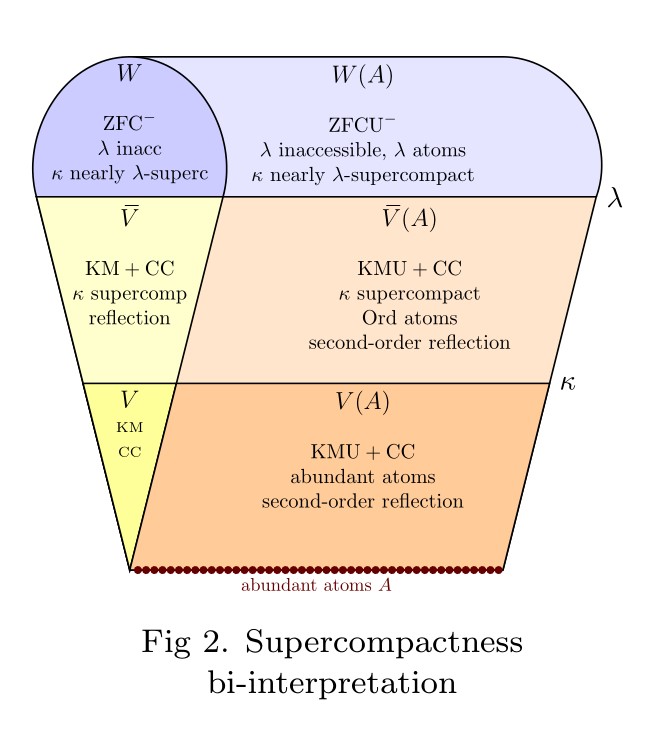
Abstract. I shall give a general introduction to urelement set theory and the role of the second-order reflection principle in second-order urelement set theory GBCU and KMU. With the abundant atom axiom, asserting that the class of urelements greatly exceeds the class of pure sets, the second-order reflection principle implies the existence of a supercompact cardinal in an interpreted model of ZFC. The proof uses a reflection characterization of supercompactness: a cardinal is supercompact if and only if for every second-order sentence

