This is a talk for the University of Wisconsin, Madison Logic Seminar, 25 January 2020 1 pm (7 pm UK).
The talk will be held online via Zoom ID: 998 6013 7362.

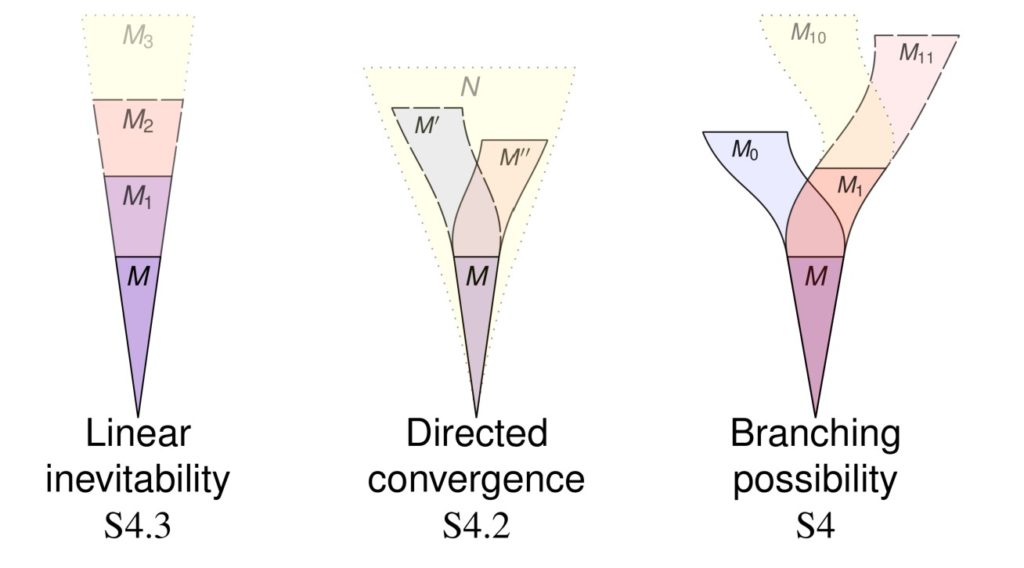
Abstract. It is a mystery often mentioned in the foundations of mathematics that our best and strongest mathematical theories seem to be linearly ordered and indeed well-ordered by consistency strength. Given any two of the familiar large cardinal hypotheses, for example, generally one of them proves the consistency of the other. Why should this be? The phenomenon is seen as significant for the philosophy of mathematics, perhaps pointing us toward the ultimately correct mathematical theories. And yet, we know as a purely formal matter that the hierarchy of consistency strength is not well-ordered. It is ill-founded, densely ordered, and nonlinear. The statements usually used to illustrate these features are often dismissed as unnatural or as Gödelian trickery. In this talk, I aim to overcome that criticism—as well as I am able to—by presenting a variety of natural hypotheses that reveal ill-foundedness in consistency strength, density in the hierarchy of consistency strength, and incomparability in consistency strength.
The talk should be generally accessible to university logic students, requiring little beyond familiarity with the incompleteness theorem and some elementary ideas from computability theory.