As a guest today in my daughter’s second-grade classroom, full of math-enthusiastic seven-and-eight-year-old girls, I led a mathematical investigation of graph coloring, chromatic numbers, map coloring and Eulerian paths and circuits. I brought in a pile of sample graphs I had prepared, and all the girls made up their own graphs and maps to challenge each other. By the end each child had compiled a mathematical “coloring book” containing the results of their explorations. Let me tell you a little about what we did.
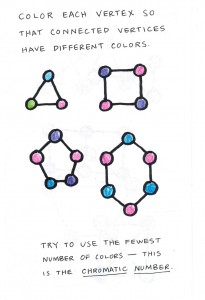
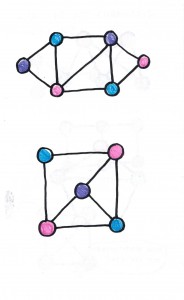
We began with vertex coloring, where one colors the vertices of a graph in such a way that adjacent vertices get different colors. We started with some easy examples, and then moved on to more complicated graphs, which they attacked.
The aim is to use the fewest number of colors, and the chromatic number of a graph is the smallest number of colors that suffice for a coloring. The girls colored the graphs, and indicated the number of colors they used, and we talked as a group in several instances about why one needed to use that many colors.
Next, the girls paired off, each making a challenge graph for her partner, who colored it, and vice versa.
Map coloring, where one colors the countries on a map in such a way that adjacent countries get different colors, is of course closely related to graph coloring.
The girls made their own maps to challenge each other, and then undertook to color those maps. We discussed the remarkable fact that four colors suffice to color any map. 
Next, we considered Eulerian paths and circuits, where one traces through all the edges of a graph without lifting one’s pencil and without retracing any edge more than once. We started off with some easy examples, but then considered more difficult cases. 
An Eulerian circuit starts and ends at the same vertex, but an Eulerian path can start and end at different vertices.
We discussed the fact that some graphs have no Eulerian path or circuit. If there is a circuit, then every time you enter a vertex, you leave it on a fresh edge; and so there must be an even number of edges at each vertex. With an Eulerian path, the starting and ending vertices (if distinct) will have odd degree, while all the other vertices will have even degree.
It is a remarkable fact that amongst connected finite graphs, those necessary conditions are also sufficient. One can prove this by building up an Eulerian path or circuit (starting and ending at the two odd-degree nodes, if there are such); every time one enters a new vertex, there will be an edge to leave on, and so one will not get stuck. If some edges are missed, simply insert suitable detours to pick them up, and again it will all match up into a single path or circuit as desired. (But we didn’t dwell much on this proof in the second-grade class.)
Meanwhile, this was an excellent opportunity to talk about The Seven Bridges of Königsberg. Is it possible to tour the city, while crossing each bridge exactly once?
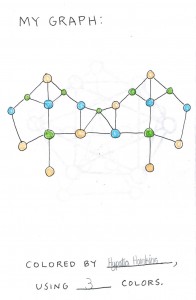
The final result: a booklet of fun graph problems!
The high point of the day occurred in the midst of our graph-coloring activity when one little girl came up to me and said, “I want to be a mathematician!” What a delight!
Andrej Bauer has helped me to make available a kit of my original uncolored pages (see also post at Google+), if anyone should want to use them to make their own booklets. Just print them out, copy double-sided (with correct orientation), and fold the pages to assemble into a booklet; a few staples can serve as a binding.
See also my followup question on MathOverflow, for the grown-ups, concerning the computational difficulty of producing hard-to-color maps and graphs.
Finally, check out my new book:
As a bit of practical advice, this was more than enough material for a one hour session. Indeed, one could easily fill an hour with just the coloring topics, saving the Eulerian paths and circuits, as well as the booklet assembly, for another session. We chose instead to leave some of the larger graphs for coloring later or at home, which I think would be good, especially if it leads to mathematical discussions at home. Another issue was that it was more complicated than I had expected to arrange for the kids to draw graphs and maps in each other’s booklets, and so some care should go into organizing this.
My 7yo daughter could understand a theorem stating that in any party there are always two kids with the same number of friends. The proof uses the pigeonhole hole principle which can be easily explained with a game where kids run around chairs and there are less chairs than kids and the kids should try to grab a chair when they hear a command.
Would love the kit.
I added a link to the kit.
Thanks so much!
So beautiful!
If mathematics was taught in this way the school would have been a thousand times more exciting…I always thought that the trick to keep the students engaged and interested is to give them interesting problem, opportunities to achieve results independently. imho..
ps:I apologize for my bad english
Thanks very much! The students seemed to like it very much, and they were excited to continue working on it when time ran out.
Thank you for coming in yesterday and providing IIAB with such a wonderful experience as they explored this investigation. It was so developmentally appropriate and exciting to watch how engaged they were.
Oh, it was my pleasure!
This is really fantastic. I am going to use this kit or some slight modification in our math circle next semester!
I’m glad to hear you liked it. I think it would work great for a math circle; let us know how it goes.
Wow. I teach 5 year olds english in japan, part of our weekly work is math, i think ill adapt some of these to our work.
Very nicely done 🙂
Domo arigatou! (Watashi mo nihon de oshiemashita, demo suugaku o oshiemashita.) I think it would work great for five-year-olds. The combination of mathematical thinking with coloring activity makes it ideal for young kids. But truthfully, I think the activity is fun for basically any age, and many parents have told me that they enjoyed completing the booklet with their kids.
This is wonderful material for a math circle! As an extension, you could also do chromatic numbers in 3D by using gumdrops and toothpicks. (I.e., a child can see that the chromatic number of a tetrahedron is 4 because it takes 4 different colors of gumdrops to build it if we follow the rule that every toothpick must have 2 different colors on its ends.)
BTW, I have a blog with other great activities for a math circle for 7 year olds:
http://1001mathproblems.blogspot.com
I like your gum drop idea!
This is great! Thanks for making the booklet available as well. Going to print it out and use it with my 8- and 6-year olds.
This is awesome! I absolutely love this and intend to do some similar activities with my 11 and 12 year olds. Thanks
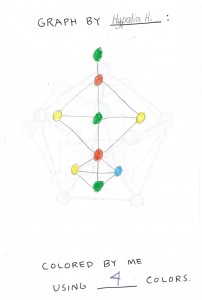
It’s nice to see you’re teaching them the Peterson graph already!
I’m glad you noticed. It is beautiful after all, and seven-year-olds can 3-color it, although they find it a challenge to do so.
so nifty, can’t wait to use with my middle school SpEd kids next year!
A friend shared this on Facebook, and as a former math teacher and later professor (and implicitly long-time math student) this is just the kind of thing that should be in the curriculum. It’s wonderful, and I’m going to bookmark this for when I get to guest lecture in my daughters’ math classes. (As an aside, I remember my father talking to my class about probability when I was in elementary school, and I wound up a mathematician, so good luck to your daughter).
I have to admit being confused by the “4 colors suffice for any map” idea. Consider the Central African Republic, which is surrounded by 6 countries. Or Niger, or Uganda…
You could color the Central African Republic purple, say, and then go red-blue-red-blue-red-blue for the surrounding countries, handling the particular case of those countries with only three colors. You may have assumed that those other six countries must use more than three colors, but in fact you only needed two for them. The four-color theorem is a wonderful, deep theorem with a rich history, which is also connected with philosophical ideas surrounding the question of what does it mean to prove something, for the simplest proofs were carried out first by computer, and led to truly enormous proof objects that could not really be checked by a human. See http://en.wikipedia.org/wiki/Four_color_theorem.
This is perfect. I am a HS math teacher with young kids. I am doing “math camp” this summer and enjoying this activity.
I’m glad to hear it. Please report back to us about it!
beautiful. Something intrigues me a lot: is there a collection of such exercises that could supplement (or ideally replace) a “normal” school curriculum, for most ages besides 8 year olds, such that these children learn and develop their math skills (and much more than that) in this beautiful way?
If there isn’t such collection compiled yet, can it be created? I can just imagine the benefits this would bring to the many children that will have the freedom and pleasure to use it.
Let’s build something like this!
would prefer if uploaded to some other place than a google drive…
I placed the pdf also on this site, so there is now a link.
Pingback: Somewhere else, part 142 | Freakonometrics
Hello, and congrats for this wonderful kit ! Do you have an objection if I translate it in French for my kids + put it on my blog with of course your refs and links ? Thanks 🙂
That would be great. Please post a link here when you’ve got it.
Here it is 🙂
http://thoughts4dads.blogspot.fr/2014/07/coloriages-de-graphes-et-nombres.html
and the PDF : http://fr.go2prod.com/wp-content/themes/imgsrc/coloriage%20de%20graphes%20et%20nombres%20chromatiques.pdf
Fantastic!
The site address has changed, it is now http://fr.toysfab.com/2014/07/coloriages-de-graphes-et-nombres-chromatiques/
This is a wonderful booklet indeed! I particularly like that in the last page, the mathematical terminology on the right side, including the reason why the answer is “no”, becomes self explanatory to any age, after reading the left side. I will translate this to Greek, German, and Spanish if that’s ok. I believe it’s terribly important to make maths interesting and fun to all ages!
Thanks, Ioanna! And please provide a link to your translations.
The graph-coloring activity worked very well with my own second grade math circle. The kids explored and noticed many interesting things, such as that a triangle has a chromatic number of 3, so any graph with an embedded triangle must need at least 3 colors. We also did some word problem applications. (E.g., You are planning a dinner party where certain people don’t get along, and you have to find the minimum number of tables you must use so that every arguing couple is separated.)
It also inspired me to find a way to do more topology with 7-year-olds. Here’s my Euler’s formula activity: http://1001mathproblems.blogspot.com/2014/07/this-weeks-puzzle.html. The trick was to find a way to ask questions so that the children are exploring the relationships and not simply learning a formula.
Thanks again for your wonderful contribution!
Great! I like your Euler’s formula post.
I have taught the seven bridges of Konigsberg to Year 10 and they seemed to find it flat and boring. I think its the way it is presented within a time poor setting, and you end up teaching formulas. I think that starting with this simple colouring approach would be a lot more fun.
I think I would change the writing to sentence case, because some children start to copy the upper case style, then get mixed up with their writing in later years.
We tried this out with our 8 year old children the other week, and they really enjoyed it and engaged with it. Thanks!
http://y4ist.blogspot.fr/2014/11/euler-week.html
(scroll to bottom of the post to see the graphs and chromatic numbers work)
I’m so glad you enjoyed it—I can see in the photos of your activities that the kids had a great time with some serious, fun math!
I was playing the chromatic number game with my 6 year old son and we came up with a 5 vertex complete graph. But that needed 5 colors?
Yes, that is right. The four-color theorem concerns only (connected) planar graphs, that is, graphs that can be drawn in the plane without any lines crossing.
Pingback: Math for eight-year-olds: graph theory for kids! | Joel David Hamkins
Pingback: June Bits and Clips | Polly Castor
Pingback: June 2014 Bits and Clips | Polly Castor
Does anyone know why knowing the chromatic number important? And which branch of mathematics is chromatic number a part of? I mean no offense or anything I’m just curious 🙂
Finding the chromatic number of a finite graph is part of finite graph theory, which is part of discrete mathematics, but also with a strong connection with finite combinatorics. In the case of infinite graphs, the study of the chromatic number of infinite graphs is part of infinite combinatorics, which is a part of set theory, and there are numerous very interesting independence results.
You ask: why is it important? For me, importance is irrelevant—rather, we study the chromatic number of various graphs just because it is fun and interesting to consider! The case of 4-coloring the planar graphs also has a very interesting history, connected with philosophical issues about the nature of proof, which arise in light of the fact that the first proofs made use of computations carried out via computer, which could not feasibly be carried out by hand.
Pingback: 135th Carnival of Mathematics | Gaurish4Math
Pingback: Coloriages de graphes et nombres chromatiques ! | Toysfab
First, thank you very much for making your work available.
Maybe this is a very silly question, but I don’t see how to print the pages of the PDF file double-sided, fold them, and then get the pages in the correct order in the booklet. For example, if page 2 is printed on the reverse side of page 1, then page 2a will be separated from page 2b by all the pages 3,…,11. From my point of view, the reverse side of page 1 should contain on the left the contents currently in page 2a, and on the right the contents currently in page 11b.
They were meant to be printed double sides, folded in half and then placed inside the outer page, as in the photo at the bottom of the post (zoom in to see how the folded pages fit together). That is how I planned it and it worked fine for me. But I realize now that this was unnecessarily confusing for many people, and so if I were to do this again, I would organize it differently.
Pingback: graph theory for children - Oxford Blog
10 years on and this is still a highly ranked result in search engines, and for good reason. Thank you for this, I am sure my son will have a great time learning this fascinating branch of mathematics 🙂
I am so glad to hear that it is appreciated!