 This will be a talk for the Dartmouth Logic Seminar on January 23rd, 2014.
This will be a talk for the Dartmouth Logic Seminar on January 23rd, 2014.
Abstract. I will discuss a number of theorems showing that the satisfaction relation of first-order logic is less absolute than might have been supposed. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic
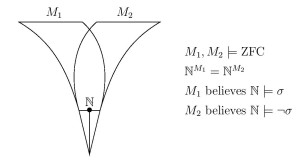 On the basis of these mathematical results, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.
On the basis of these mathematical results, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.
Main article: Satisfaction is not absolute

