Welcome to my latest instance of Math for Kids!
Today I had the pleasure to make an interactive mathematical presentation at my son’s school to the 7th / 8th grade Math Team, about 30 math-enthusiastic kids (twelve and thirteen years old) along with their math teachers and the chair of the school math department.
The topic was the game of Nim! This game has a secret mathematical strategy enabling anyone with that secret knowledge to win against those without it. It is a great game for kids, because with the strategy they can realistically expect to beat their parents, friends, siblings and parent’s friends almost every single time!

To play Nim, one player sets up a number of piles of blocks, and the opponent chooses whether to go first or second. The players take turns removing blocks — each player may remove any number of blocks (at least one) from any one pile, and it is fine to take a whole pile — whichever player takes the last block wins.
For the math team, we played a few demonstration games, in which I was able to beat all the brave challengers, and then the kids paired off to play each other and gain familiarity with the game. Then, it was time for the first strategy discussion.
What could the secret winning strategy be? I explained to the kids a trick that mathematicians often use when approaching a difficult problem, namely, to consider in detail some very simple special cases or boundary instances of the problem. It often happens that these special cases reveal a way of thinking about the problem that applies much more generally.
Perhaps one of the easiest special cases of Nim occurs when there is only one pile. If there is only one pile, then clearly one wants to go first, in order to make the winning move: take the entire pile!

Two balanced piles
A slightly less trivial and probably more informative case arises when there are exactly two piles. If the stacks have the same height, then the kids realized that the second player could make copying moves so as to preserve this balanced situation. The key insight now is that this copying strategy is a winning strategy, because if one can always copy, then in particular one will have a move whenever the opponent did, and so the opponent will never take the last block. With two piles, therefore, one wants always to make them balanced. If they are initially unbalanced, then choose to go first and follow the balancing strategy. If they are initially balanced, then choose to go second, and copy whatever moves your opponent makes to rebalance them.

A balanced position
With that insight, it is not difficult to see that it is winning to leave a position with any number of pairs of balanced piles. One can in effect play on each pair separately, because whenever the opponent makes a move on one of the piles, one can copy the move with the corresponding partner pile. In this way, we may count such a position overall as balanced. The more fundamental game-theoretic observation to make is that balanced piles in effect cancel each other out in any position, and one can ignore them when analyzing a position. When two balanced piles are present in a possibly more complicated position, one can pretend that they aren’t there, precisely because whenever your opponent plays on one of them, you can copy the move on the other, and so any winning strategy for the position in which those piles are absent can be converted into a winning strategy in which the balanced piles are present.
This idea now provides a complete winning strategy in the case that all piles have height one or two at most. One wants to leave a position with an even number of piles of each height. If only one height has an odd number of piles, then take a whole pile of that height. And if there are odd numbers of piles both of height one and two, then turn a height-two pile into a pile of height one, and this will make them both even. So any unbalanced position can be balanced, and any move on a balanced position will unbalance it.

1+2+3 counts as balanced
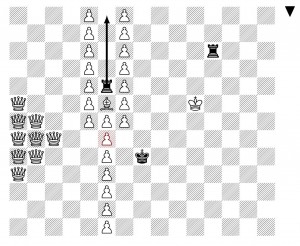
Let’s now consider that there may be piles of height three. For example, consider the basic position with piles of height one, two and three. The observation to make here is that any move on this position can be replied to with a move that leaves it balanced (check it yourself to be sure!). It follows that this position is winning to leave for the other player (and so one should go second on
This way of thinking produces a complete winning strategy for Nim positions involving piles of height at most three. (And this is a strategy that can be mastered even by very young children — a few years ago I had talked about Nim with much younger children, Math for six-year-olds: Win at Nim!, first-graders at my daughter’s school, and at that time we concentrated on posititions with piles of height at most three. Older kids, however, can handle the full strategy.) Namely, the winning strategy in this case is to strive to balance the position, to make an even number overall of piles of height one and two, where we count piles of height three as one each of one and two. If you always give your opponent a balanced position, then you will win! Faced with an unbalanced position, it is a fact that you can always find a balancing move, and any move on an balanced position will unbalance it. If the game is just starting, and you are deciding whether to go first or second, you should determine whether it is balanced yet or not. If it unbalanced, then you should go first and make the balancing move; if it is already balanced, then you should go second and adopt the copying strategy, in which you re-balance the position with each move.
The general winning strategy, of course, goes beyond three. The key idea is to realize that what is really going on when we represent 
The general strategy is to view every Nim pile as consisting of subpiles whose height is a power of two, and to make sure that one leaves a position that is balanced in the sense that every power of two has an even number of such instances in the position. So we think of
The mathematical facts to verify are (1) any move on a balanced position in this powers-of-two sense will cause it to become unbalanced, and (2) any unbalanced position can be balanced in one move. It follows that leaving balanced positions is a winning strategy, because the winning move of taking the last block is a balancing move rather than an unbalancing move.
One can prove statement (1) by realizing that when you move a single stack, the binary representation changes, and so whichever binary digits changed will now become unbalanced. For statement (2), consider the largest unbalanced power of two
As a practical matter, the proof of (2) also shows how one can find a (winning) balancing move, which can otherwise be difficult in some cases: look for the largest unbalanced power of two, and move on any pile containing such a subpile, making sure to leave a balanced position.
In most actual instances of Nim, the pile heights are rarely very tall, and so one is usually considering just
It is interesting to consider also the Misère form of Nim, where one wants NOT to take the last block. This version of the game also has a secret mathematical strategy, which I shall reveal later on.
Challenge 1. What is the winning strategy in Misère Nim?
If you figure it out, please post a comment! I’ll post the solution later. One might naively expect that the winning strategy of Misère Nim is somehow totally opposite to the winning strategy of regular Nim, but in fact, the positions
Another interesting generalization, for the set-theorists, is to consider transfinite Nim, where the piles can have transfinite ordinal height. So we have finitely many piles of ordinal height, perhaps infinite, and a move consists of making any one pile strictly shorter. Since there are no infinite descending sequence of ordinals, the game will terminate in finitely many moves, and the winner is whowever removes the last block.
Challenge 2. Who wins the transfinite Nim game with piles of heights:
Post your solutions! You can also see my solution and further discussion.