Tag Archives: chess

Checkmate is not the same as a forced capture of the enemy king in simplified chess

Posted on by
5

In my imagination, and perhaps also in historical reality, our current standard rules of chess evolved from a simpler era with a simpler set of rules for the game. Let us call it simplified chess. In simplified chess there was the same 8×8 board with the same pieces as now moving under the same movement rules. But the winning aim was different, and simpler. Namely, the winning goal of simplified chess was simply to capture the enemy king. You won the game by capturing the opposing king, just as you would capture any other piece.

There was therefore no need to mention check or checkmate in the rules. Rather, these words described important situations that might arise during game play. Specifically, you have placed your opponent in check, if you were in a position to capture their king on the next move, unless they did something to prevent it. You placed your opponent in checkmate, if there was indeed nothing that they could do to prevent it.

In particular, in simplified chess there was no rule against leaving your king in check or even moving your king into check. Rather, this was simply an inadvisable move, because your opponent could take it and thereby win. Checkmate was merely the situation that occurred when all your moves were like this.

It is interesting to notice that it is common practice in blitz chess and bullet chess to play with something closer to simplified chess rules—it is often considered winning simply to capture the opposing king, even if there was no checkmate. This is also how the chess variant bughouse is usually played, even in official tournaments. To my way of thinking, there is a certain attractive simplicity to the rules of simplified chess. The modern chess rules might seem to be ridiculous for needlessly codifying into the rules a matter that could simply be played out on the board by actually capturing the king.

Part of what I imagine is that our contemporary rules could easily have evolved from simplified chess from a practice of polite game play. In order to avoid the humiliation of actually capturing and removing the opponent’s king and replacing it with one’s own piece, which indeed might even have been a lowly pawn, a custom developed to declare the game over when this was a foregone conclusion. In other words, I find it very reasonable to suppose that the winning checkmate rule simply arose from a simplified rule set by common practice of respectful game play.

I am not a chess historian, and I don’t really know if chess did indeed evolve from a simpler version of the game like this, but it strikes me as very likely that something like this must have happened. I await comment from the chess historians. Let me add though that I would also find it reasonable to expect that simplified chess might also have had no provision for opening pawns moving two squares instead of just one. Such a rule could arise naturally as an agreed upon compromise to quicken the game and get to the more interesting positions more quickly. But once that rule was adopted, then the en passant rule is a natural corrective to prevent abuse. I speculate that castling may have arisen similarly—perhaps many players in a community customarily took several moves, perhaps in a standard manuver sequence, to accomplish the effect of hiding their kings away toward the corner and also bringing their rooks to the center files; the practice could have simply been codified into a one-move practice.

My main point in this post, however, does not concern these other rules, but rather only the checkmate winning condition rule and to a certain logic-of-chess issue it brings to light.

When teaching chess to beginners, it is common to describe the checkmate winning situation in terms of the necessary possibility of capturing the king. One might say that a checkmate situation means the king is attacked, and there is nothing the opponent can do to prevent the king from being captured.

This explanation suggests a general claim in the logic of chess: a position is in checkmate (in the contemporary rules) if and only if the winning player can necessarily capture the opposing king on the next move (in simplified chess).

This claim is mostly true. In most instances, when you have placed your opponent in checkmate, then you would be able to capture their king on your next move in simplified chess, since all their moves would leave the king in check, and so you could take it straight away.

But I would like to point out something I found interesting about this checkmate logic claim. Namely, it isn’t true in all cases. There is a position, I claim, that is checkmate in the modern rules, but in simplified chess, the winning player would not be able to capture the enemy king on the next move.

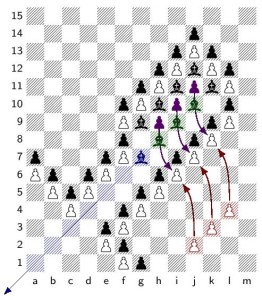
My example proceeds from the following (rather silly) position, with black to move. (White pawns move upward.)

Of course, Black should play the winning move: knight to C7, as shown here:

This places the white king in check, and there is nothing to be done about it, and so it is checkmate. Black has won, according to the usual chess rules of today.

But let us consider the position under the rules of simplified chess. Will Black be able to capture the white king? Well, after Black’s nC7, it is now White’s turn. Remember that in simplified chess, it is allowed (though inadvisable) to leave one’s king in check at the end of turn or even to move the king into check. But the trouble with this position is not that White can somehow move to avoid check, but rather simply that White has no moves at all. There are no White moves, not even moves that leave White in check. But therefore, in simplified chess, this position is a stalemate, rather than a Black win. In particular, Black will not actually be able to capture the White king, since White has no moves, and so the game will not proceed to that juncture.

Conclusion: checkmate in contemporary chess is not always the same thing as being necessarily able to capture the opposing king on the next move in simplified chess.

Of course, perhaps in simplified chess, one wouldn’t regard stalemate as a draw, but as a win for the player who placed the opponent in stalemate. That would be fine by me (and it would align with the rules currently used in draughts, where one loses when there is no move available), but it doesn’t negate my point. The position above would still be a Black win under that rule, sure, but still Black wouldn’t be able to capture the White king. That is, my claim would stand that checkmate (in modern rules) is not the same thing as the necessary possibility to capture the opposing king.

I had made a Tweet earlier today about this idea (below), but opted for a fuller explanation in this blog post to explain the idea more carefully.

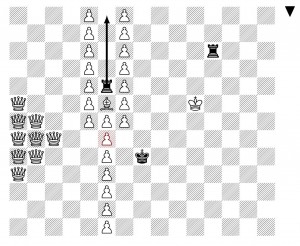
On Twitter, user Gro-Tsen pointed out a similar situation arises with stalemates. Namely, consider the following position, with White to play:

Perhaps Black had just played qB5, which perhaps was a blunder, since now the White king sits in stalemate, with no move. So in the usual chess rules, this is a drawn position.

But in simplified chess, according to the rules I have described, the White king is not yet explicitly captured, and so he is free still to move around, to A6, A8, B6, or B7 (moving into check), or also capturing the black rook at B8. But in any case, whichever move White makes, Black will be able to capture the White king on the next move. So in the simplified chess rules, this position is White-to-win-in-1, and not a draw.

Furthermore, this position therefore shows once again that checkmate (in normal rules) is not the same as the necessary possibility to capture the king (in simplified rules), since this is a position where Black has a necessary possibility to capture the White king on the next move in simplified chess, but it is not checkmate in ordinary chess, being rather stalemate.

;TLDR Ultimately, my view is that our current rules of chess likely evolved from simplified rules and the idea that checkmate is what occurs when you have a necessary possibility of capturing the enemy king on the next move in those rules. But nevertheless, example chess positions show that these two notions are not quite exactly the same.

My favorite theorem

Posted on by
2

What a pleasure it was to be interviewed by Evelyn Lamb and Kevin Knudson for their wonderful podcast series, My Favorite Theorem, available on Apple, Spotify, and any number of other aggregators.

I had a chance to talk about one my most favorite theorems, the fundamental theorem of finite games.

Theorem.(Zermelo 1913) In any two-player finite game of perfect information, one of the players has a winning strategy, or both players have drawing strategies.

Listen to the podcast here: My Favorite Theorem. A transcript is also available.

What is the game of recursive chess?

Posted on by
18

Consider this fascinating vision of recursive chess — the etching below was created by Django Pinter, a tutorial student of mine who has just completed his degree in the PPL course here at Oxford, given to me as a parting gift at the conclusion of his studies. Django’s idea was to play chess, but in order for a capture to occur successfully on the board, as here with the black Queen attempting to capture the opposing white knight, the two pieces would themselves sit down for their own game of (recursive) chess. The idea was that the capture would be successful only in the event that the subgame was won. Notice in the image that not only is there a smaller recursive game of chess, but also a still tinier subrecursive game below that (if you inspect closely), while at the same time larger pieces loom in the background, indicating that the main board itself is already several levels deep in the recursion.

The recursive chess idea may seem clear enough initially, and intriguing. But with further reflection, we might wonder how does it work exactly? What precisely is the game of recursive chess? This is my question here.

My goal with this post is to open a discussion about what ultimately should be the precise the rules and operations of recursive chess. I’m not completely sure what the best rule set will be, although I do offer several proposals here. I welcome further proposals, commentary, suggestions, and criticism about how to proceed. Once we settle upon a best or most natural version of the game, then I shall hope perhaps to prove things about it. Will you help me decide what is the game of recursive chess?

Let me describe several natural proposals:

Naïve recursion. Although this seems initially to be a simple, sound proposal, ultimately I find it problematic. The naïve idea is that when one piece wants to capture another in the game at hand, then the two pieces themselves play a game of chess, starting from the usual chess starting position. I would find it natural that the attacking piece should play as white in this game, going first, and if that player wins the subgame, then the capture in the current game is successful. If the subgame is a loss, then the capture is unsuccessful.

There seem, however, to be a variety of ways to handle the losing subgame outcome, and since these will apply with several of the other proposals, let me record them here:

  • Failed-capture. If the subgame is lost, then the capture in the current game simply does not occur. Both pieces remain on their original squares, and the turn of play passes to the opponent. Notice that this will have serious affects in certain chess situations involving zugswang, a position where a player has no good move — because if one of them is a capture, then the player can aim to play badly in the subgame and thereby legally pass the turn of play to the opponent without having made any move. This situation will in effect cause the subgame players to attempt to lose, rather than win, which seems undesirable.
  • Failed-capture-with-penalty. If the subgame is lost, then the capture does not occur, but furthermore, the attacking piece is itself lost, removed from the board, and the turn of play passes to the opponent. In effect, under this rule, every attempt at capture is putting the life of the capturing piece at risk, which makes a certain amount of sense from a military point of view. I think perhaps this is a good rule.
  • Failed-capture-with-retry. If the subgame is lost, then the capture does not occur, but both pieces remain on their original squares, and the attacking player is allowed to proceed with another (different) move. Attempting the same attack from the same board position multiple times is subject to the three-fold repetition rule. This interpretation amounts in effect to the game play searching a large part of the game tree, exploring the possible capturing moves, but with the first successful option fixed as official. It invites manipulation by the opponent, who might play badly against a misguided capture attempt, causing it to be fixed as the official move.
  • Drawn subgame. A further complication arises from the fact that the subgame can itself be drawn, rather than won. Is this sufficient to cause the penalty or the retry? Or does this count as a failed capture?

As I see it, however, the principal problem with the naïve recursion rule is that it seems to be ill-founded. After all, we can have a game with a capture, which leads to a subgame with a capture, which leads to a deeper subgame with a capture, and so on descending forever. How is the outcome determined in this infinitely descending situation? None of the subgames is ever resolved with a definite conclusion until all of them are, and there seems no coherent way to assign resolutions to them. All infinitely many subgames are simply left hanging mid-play, and indeed mid-move. For this reason, the naïve recursion idea seems ultimately incoherent to me as a game rule.

What we would seem to need instead is a well-founded recursion, one which would ultimately bottom-out in a base case. With such a recursion, every outcome of the game would be well-defined. Such a well-founded recursion would be achieved, for example, if on every subgame there were strictly fewer pieces. Eventually, the subgames would reduce to king versus king, a drawn game, and then the drawn subgame rule would be invoked to whatever affect it cause. But the recursion would definitely terminate. And perhaps most recursions would terminate because the stronger player was ultimately mating in all his attacks, without requiring any invocation of the drawn subgame rule.

We can easily describe several natural subgame positions with one fewer piece. For example, when one piece attacks another, we may naturally consider the positions that would result if we performed the capture, or if we removed the attacking piece; and we might further consider swapping the roles of the players in these positions. Such cases would constitute a well-founded recursion, because the subgame position would have fewer pieces than the main position. In this way, we arrive at several natural recursion rules for recursive chess.

Proof-of-sufficiency recursion. The motivating idea of this recursion rule is that in order for an attack to be successful, the attacking player must prove that it will be sufficient for the attack to be successful. So, when piece A attacks piece B in the game, then a subgame is set up from the position that would result if A were successfully to capture B, and the players proceed in the game in which the attack has occurred. This is the same as proceeding in the main game, under the assumption that the attack was successful. If the attacking player can win this subgame, then it shows in a sense the sufficiency of the attack as a means to win, and so on the proof-of-sufficiency idea, we allow this as a reason for the attack to have been successful.

One might object that this recursion seems at first to amount to just playing chess as usual, since the subgame is the same as the original game with the attack having succeeded. But there is a subtle difference. For a misguided attack, the attacked player can play suboptimally in the subgame, intentionally losing that game, and then play differently in the main game. There is, of course, no obligation that the players respond the same at the higher-level games as in the lower games, and this is all part of their strategic calculation.

Proof-of-necessity recursion. The motivating idea of this recursion rule, in contrast, is that in order for an attack to be successful, the attacking player must prove that it is necessary that the attack take place. When piece A attacks piece B in the main game, then a subgame is set up in which the attack has not succeeded, but instead the attacking piece is lost, but the color sides of the players are swapped. If a black Queen attacks a white knight, for example, then in the subgame position, the queen is removed, and the players proceed from that positions, but with the opposite colors. By winning this subgame, the attacking player is in effect demonstrating that if the attack were to fail, then it would be devastating for them. In other words, they are demonstrating the necessity of the success of the attack.

For the both the proof-of-sufficiency and the proof-of-necessity versions of the recursion, it seems to me that any of the three failed-capture rules would be sensible. And so we have quite a few different interpretations here for what is the game of recursive chess.

What is your proposal? Please let me know in the comments. I am interested to hear any comments or criticism.

Draw an infinite chessboard in perspective, using straightedge only

Posted on by
5

I’d like to explain to you how to draw chessboards by hand in perfect perspective, using only a straightedge.  In this post, I’ll explain how to construct chessboards of any size, starting with the size of the basic unit square.

This post follows up on the post I made yesterday about how to draw a chessboard in perspective view, using only a straightedge.  That method was a subdivision method, where one starts with the boundary of the desired board, and then subdivides to make a chessboard. Now, we start with the basic square and build up. This method is actually quite efficient for quickly making very large boards in perspective view.

I want to emphasize that this is something that you can actually do, right now. It’s fun! All you need is a piece of paper, a pencil and a straightedge. I’ll wait right here while you gather your materials. Use a ruler or a chop stick (as I did) or the edge of a notebook or the lid of a box. Sit at your table and draw a huge chessboard in perspective. You can totally do this.

Start with a horizon, having two points at infinity (orange), at left and right, and a third point midway between them (brown), which we will call the diagonal infinity. Also, mark the front corner of your chess board (blue).

Extend the front corner to the points at infinity. And then mark off (red) a point that will be a measure of the grid spacing in the chessboard. This will the be size of the front square.

You can extend that point to infinity at the right. This delimits the first rank of the chessboard.

Next, extend the front corner of the board to the diagonal infinity.

The intersection of that diagonal with the previous line determines a point, which when extended to infinity at the left, produces the first square of the chessboard.

And that line determines a new point on the leading rank edge. Extend that point up to the diagonal infinity, which determines another point on the second rank line.

 

Extend that line to infinity at the left, which determines another point on the leading rank edge.

Continuing in this way, one can produce as many first rank squares as desired. Go ahead and do that. At each step, you extend up to the diagonal infinity, which determines a new point, which when extended to infinity at the left determines another point, and so on.

If you should now reflect on the current diagram, you may notice that we have actually determined many further points in the grid than we have mentioned — and thanks to my daughter Hypatia for noticing this simplification — for there is a whole triangle of further intersection points between the files and the diagonals.

We can use these points (and we do not need them all) to construct the rest of the board, by drawing out the lines to infinity at the right. Thus, we construct the whole chessboard:

One can construct a perspective chessboard of any size this way, and one can simply continue with the construction and make it larger, if desired.

It will look a little better if you add a point at infinity down below (and do so directly below the diagonal point at infinity, but a good distance down below the board), and extend the board downward one level. The corresponding diagram on yesterday’s post might be helpful.

 

You can now color the tile pattern, and you’ll have a chessboard in perfect perspective view.

 

If you keep going, you can make extremely large chessboards. In time, I hope that you will come to learn how to complete an infinite chess board in finite time.