This will be accessible online talk about infinite chess and other infinite games for the Talk Math With Your Friends seminar, June 18, 2020 4 pm EST (9 pm UK). Zoom access information. Please come talk math with me!
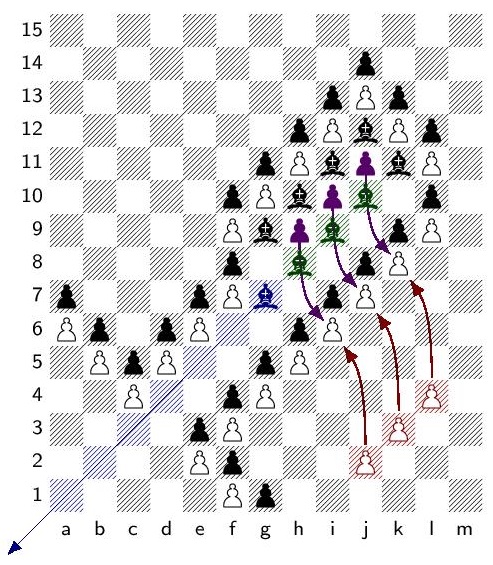
Abstract. I will give an introduction to the theory of infinite games, with examples drawn from infinite chess in order to illustrate various concepts, such as the transfinite game value of a position.
See more of my posts on infinite chess.


Very excited! Thanks for doing this!
Nice talk, I haven’t read the papers carefully but the slides are a good summary. I didn’t realize the “white wins” question had unknown and possibly very high (hyperarithmetic etc.) complexity. What I had wondered was whether it was possible to encode an arbitrary arithmetic sentence as an infinite chess position (finite number of pieces on infinite board) such that the sentence is true iff white wins. Since this is apparently unknown, does it seem likely that the rules of chess could be modified to make it straightforwardly possible, while still looking something like chess? I think it is philosophically interesting because it gives a way to see sentences with high quantifier complexity as meaningful. Thanks.