A joint paper with Davide Leonessi, in which we prove that every countable ordinal arises as the game value of a position in infinite draughts, and this result is optimal for games having countably many options at each move. In short, the omega one of infinite draughts is true omega one.
[bibtex key=”HamkinsLeonessi:Transfinite-game-values-in-infinite-draughts”]
Download the paper at arXiv:2111.02053
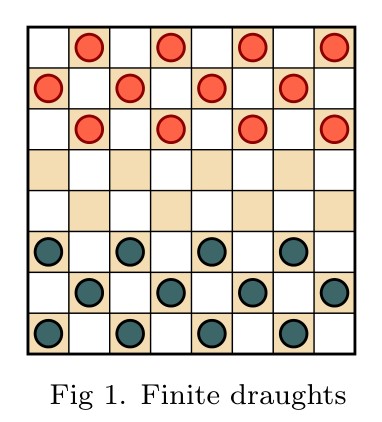
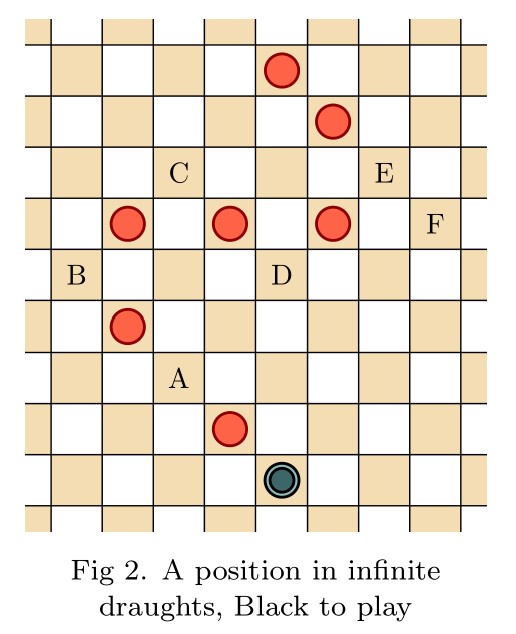
Abstract. Infinite draughts, or checkers, is played just like the finite game, but on an infinite checkerboard extending without bound in all four directions. We prove that every countable ordinal arises as the game value of a position in infinite draughts. Thus, there are positions from which Red has a winning strategy enabling her to win always in finitely many moves, but the length of play can be completely controlled by Black in a manner as though counting down from a given countable ordinal.
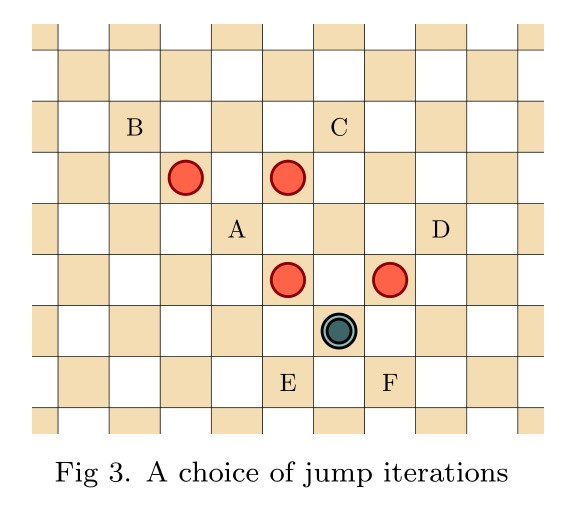
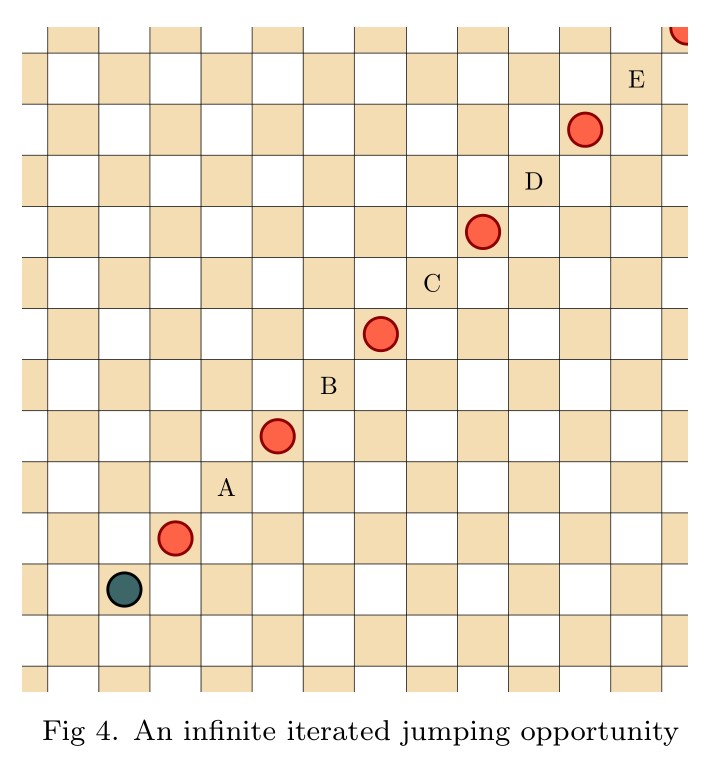
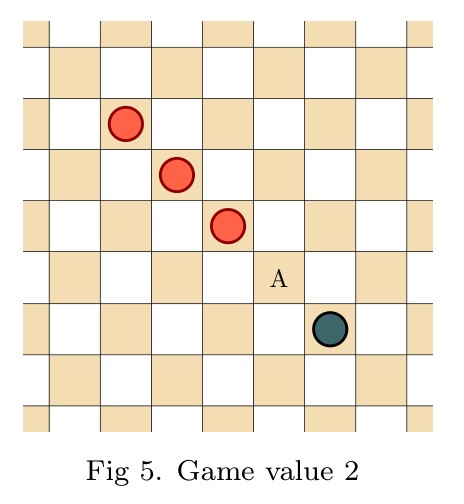
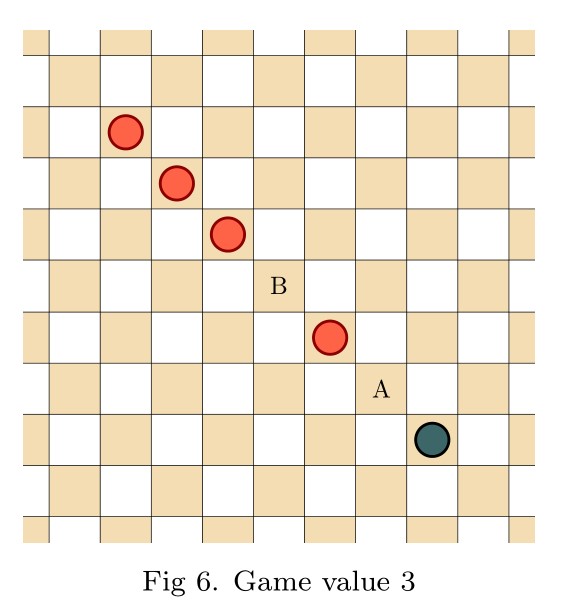
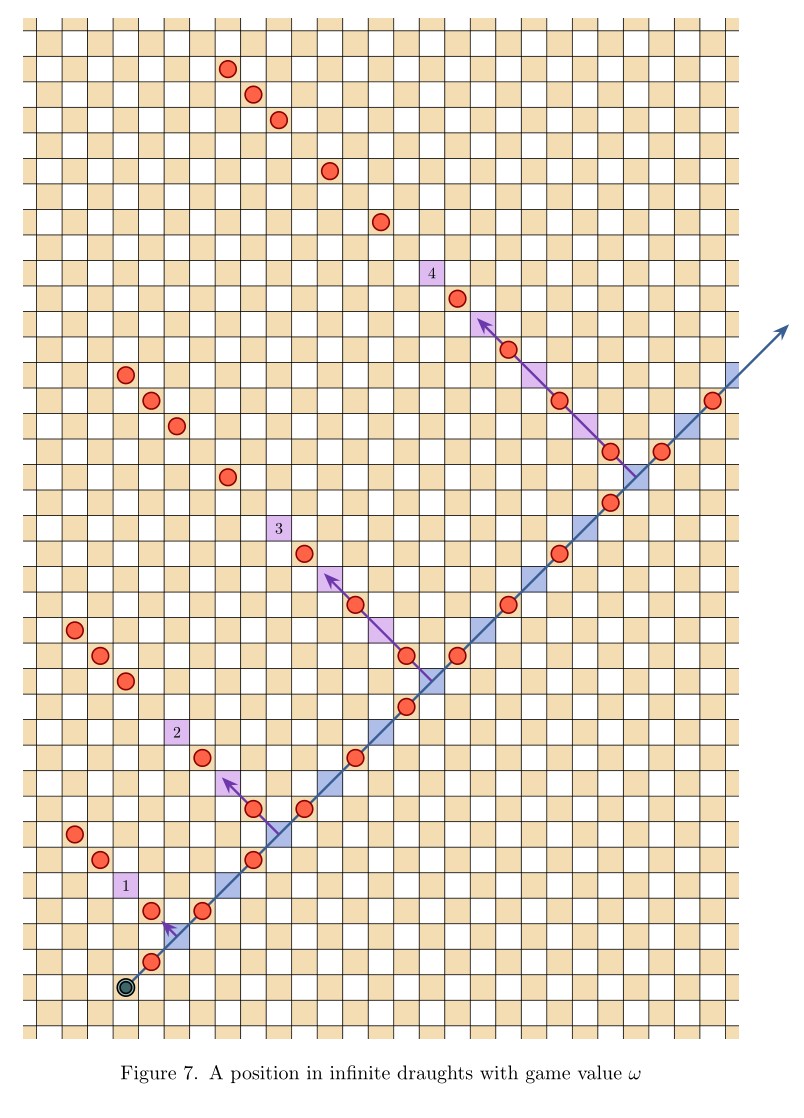
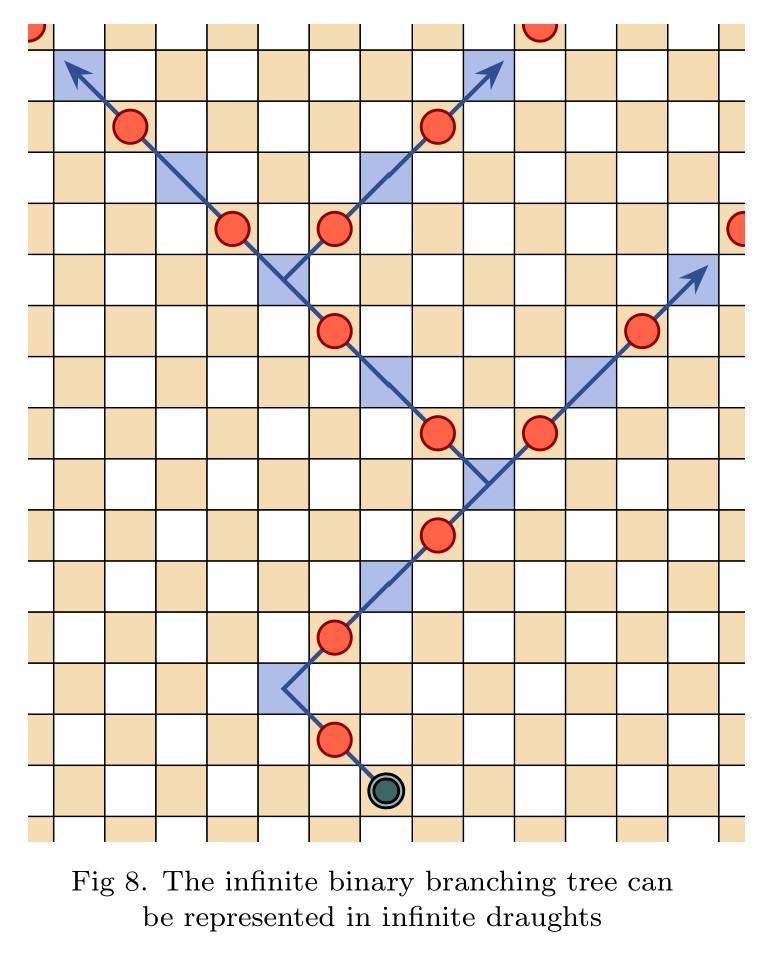
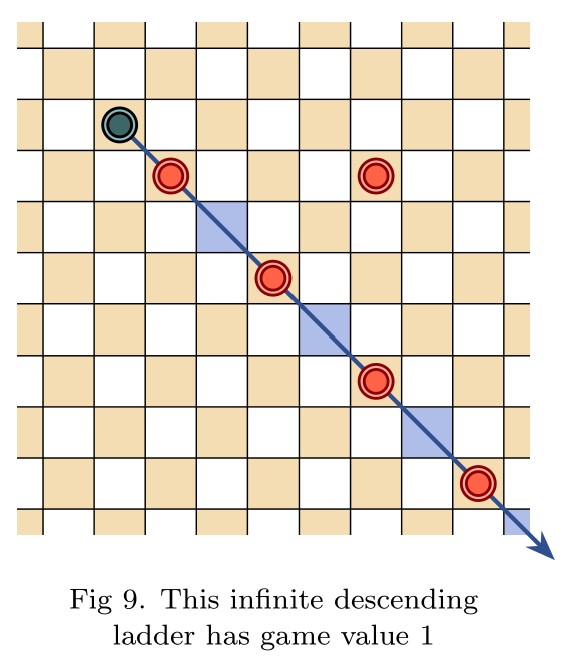
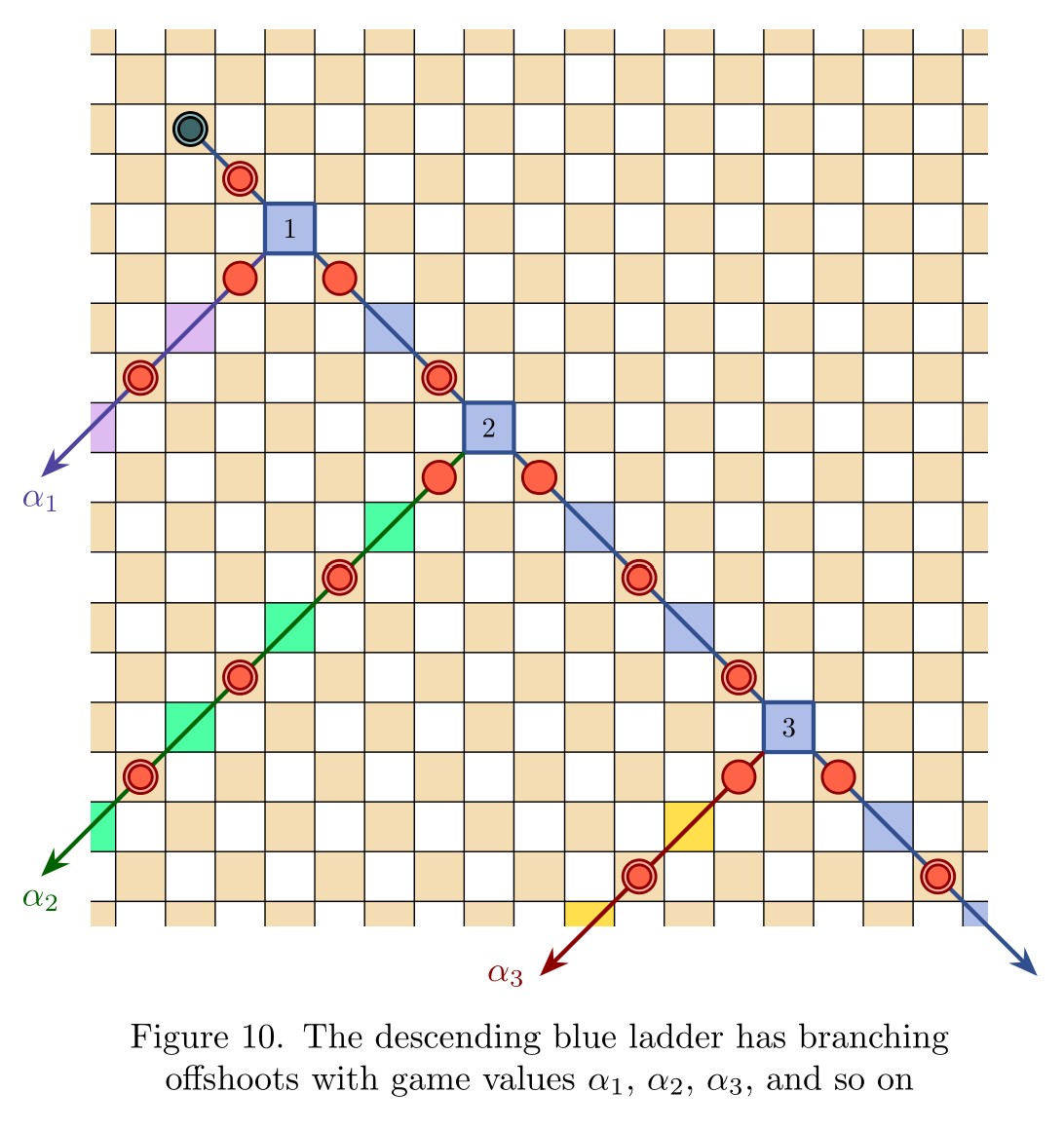


Pingback: Infinite Hex is a draw | Joel David Hamkins
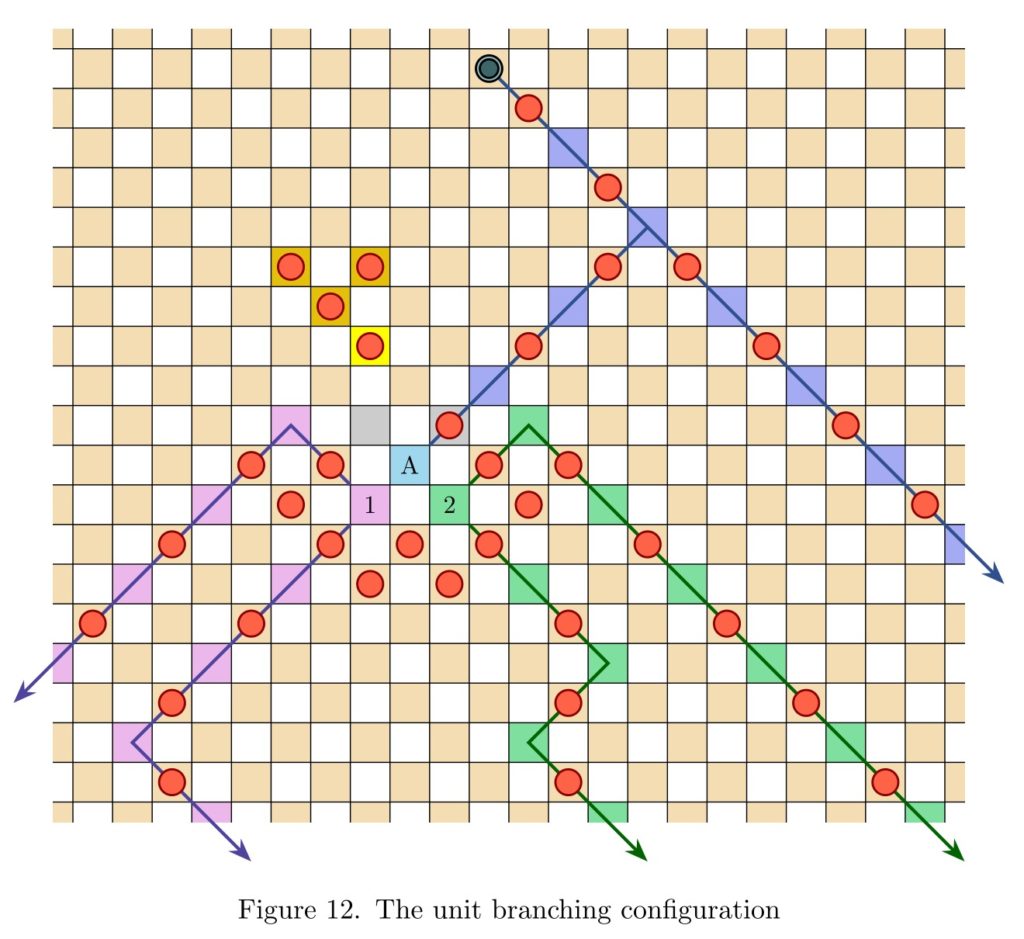
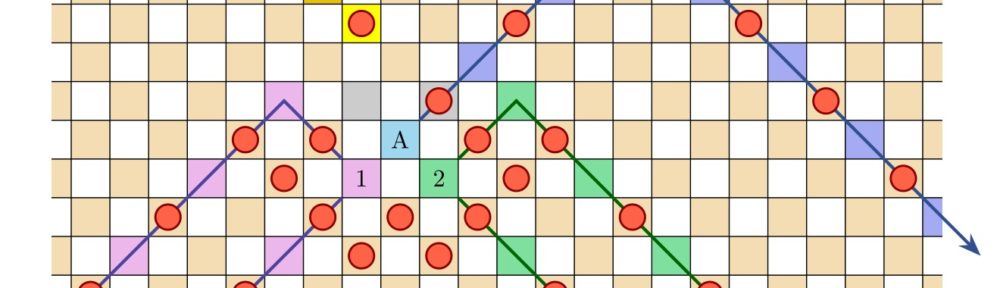
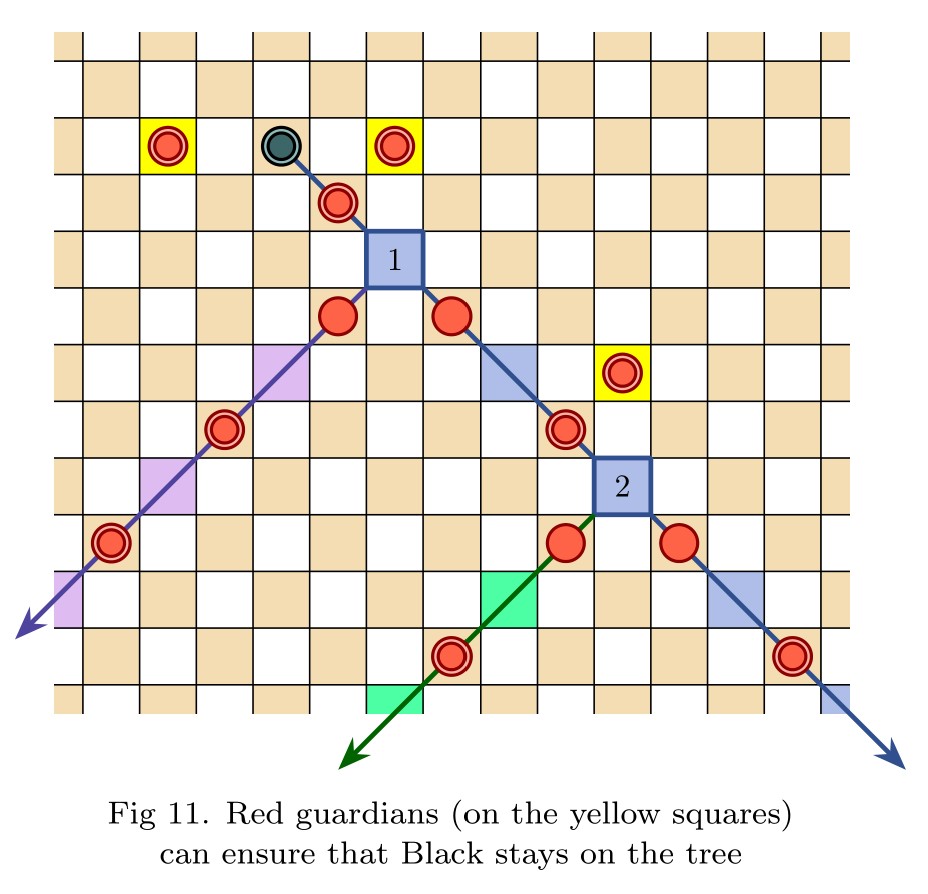
Am I right that when we embed the full infinite binary tree into the board we let branches grow in a zigzag fashion — until they have enough space to branch again?
I also wonder why the same trick doesn’t work in infinite chess. It seems we can embed the full binary tree in chess as well. In 3d version there was a black bishop in a layer that could unblock a finite straight path for the black king to pass. Maybe there is a way to put a number of bishops so that they can unblock a zigzag path for the king (in a single plane).
The reason the trick doesn’t work in chess is that one cannot move around the zig-zag corners on a single move (but in draughts, this is no problem). Thus, the possibility of a draw by infinite play enters the picture, which ruins the analysis. Meanwhile, in 3D chess, Cory Evans and I proved that we can put the branches on separate layers, keeping them straight, and the analysis works.